Chuyên đề Xác suất lớp 11 (Chân trời sáng tạo)
Tài liệu chuyên đề Xác suất trong Chuyên đề dạy thêm Toán 11 Chân trời sáng tạo gồm các dạng bài tập từ cơ bản đến nâng cao với phương pháp giải chi tiết và bài tập tự luyện đa dạng giúp Giáo viên có thêm tài liệu giảng dạy Toán 11.
Chuyên đề Xác suất lớp 11 (Chân trời sáng tạo)
Chỉ từ 200k mua trọn bộ Chuyên đề dạy thêm Toán 11 Chân trời sáng tạo bản word có lời giải chi tiết:
- B1: gửi phí vào tk:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án
Bài 1. Biến cố giao và quy tắc nhân xác suất
I. LÝ THUYẾT
1. BIẾN CỐ GIAO
Cho A và B là hai biến cố. Biến cố: “Cả A và B xảy ra”, kí hiệu AB hoặc được gọi là biến cố giao của A và B.
Chú ý: Tập hợp mô tả biến cố AB là giao của hai tập hợp mô tả biến cố A và biến cố B. Biến cố AB xảy ra khi và chỉ khi cả hai A và B xảy ra.
2. HAI BIẾN CỐ XUNG KHẮC.
Hai biến cố A và B được là xung khắc nếu A và B không đồng thời xảy ra.
Chú ý: Hai biến cố A và B là xung khắc khi và chỉ khi
Ví dụ 1: Một hộp có 5 viên bi xanh, 4 viên bi đỏ và 2 viên bi vàng. Lấy ra ngẫu nhiên đồng thời 2 viên bi từ hộp. Hãy xác định các cặp biến cố xung khắc trong các biến cố sau:
A : “Hai viên bi lấy ra cùng màu xanh”
B : “Hai viên bi lấy ra cùng màu đỏ”
C : “Hai viên bi lấy ra cùng màu”
D : “Hai viên bi lấy ra khác màu”
Giải
Ta có hai biến cố A và B xung khắc
Biến cố C xảy ra khi lấy ra 2 viên bi xanh hoặc 2 viên bi đỏ hoặc 2 viên bi vàng. Khi lấy được 2 viên bi màu xanh thì biến cố A và biến cố C cùng xảy ra. Khi lấy được 2 viên bi màu đỏ thì biến cố B và biến cố C cùng xảy ra. Do đó biến cố C không xung khắc với biến cố A và biến cố B.
Biến cố D xảy ra khi lấy ra 1 viên bi xanh, 1 viên bi đỏ ; hoặc 1 viên bi xanh, 1 viên bi vàng ; hoặc 1 viên bi đỏ, 1 biên bi vàng. Do đó biến cố D xung khắc với biến cố A, xung khắc với biến cố B và xung khắc với biến cố C.
Vậy có 4 cặp biến cố xung khắc là: A và B ; A và D; B và D; C và D.
3. BIẾN CỐ ĐỘC LẬP
Hai biến cố A và B được gọi là độc lập nếu việc xảy ra hay không xảy ra biến cố này không làm ảnh hưởng tới xác suất xảy ra của biến cố kia.
Nhận xét: Nếu hai biến cố A và B độc lập thì A và ; và B; và cũng độc lập.
Ví dụ 2. Trong hộp có một quả bóng xanh, 1 quả bóng đỏ, 1 quả bóng vàng. Lấy ra ngẫu nhiên 1 quả bóng, xem màu rồi trả lại hộp. Lặp lại phép thử trên 2 lần và gọi là biến cố quả bóng lấy ra lần thứ k là quả bóng xanh .
a) có là các biến cố độc lập không? Tại sao?
b) Nếu trong mỗi phép thử trên ta không trả bóng lại hộp thì có là các biến cố độc lập không? Tại sao?
Giải
a) Nếu xảy ra thì sau khi trả lại quả bóng thứ nhất vào hộp, trong hộp có 1 quả bóng xanh, 1 quả bóng đỏ và 1 quả bóng vàng, do đó xác suất xảy ra là .
Ngược lại, nếu không xảy ra thì sau khi trả lại quả bóng thứ nhất vào hộp, trong hộp vẫn có 1 quả bóng xanh, 1 quả bóng đỏ và 1 quả bóng vàng, do đó xác suất xảy ra là .
Ta thấy khi xảy ra hay không xảy ra thì xác suất của biến cố luôn bằng . Do quả bóng lấy ra lần thứ nhất được trả lại hộp nên biến cố xảy ra hay không xảy ra không ảnh hưởng đến xác suất xảy ra của . Vậy và là hai biến cố độc lập.
b) Giả sử quả bóng lấy ra lần đầu tiên không trả lại hộp.
Nếu xảy ra thì trước khi bốc quả bóng thứ hai, trong hộp có 1 quả bóng đỏ, 1 quả bóng vàng. Do đó xác suất xảy ra là 0.
Ngược lại, nếu không xảy ra thì trước khi bốc quả bóng thứ hai, trong hộp có 2 quả bóng, trong đó có đúng 1 quả bóng xanh. Do đó xác suất xảy ra là .
Ta thấy xác suất xảy ra của biến cố phụ thuộc vào sự xảy ra của . Vậy và không là hai biến cố độc lập.
4. QUY TẮC NHÂN XÁC SUẤT CỦA HAI BIẾN CỐ ĐỘC LẬP
Để tính xác suất của giao các biến cố độc lập, ta sử dụng quy tắc nhân xác suất sau:
Nếu hai biến cố A và B độc lập thì .
Chú ý: Từ quy tắc nhân xác suất ta thấy, nếu thì hai biến cố A và B không độc lập.
Ví dụ 3. Cho A và B là hai biến cố độc lập. Biết . Hãy tính xác suất của các biến cố .
Giải
Do A và B là hai biến cố độc lập nên .
Ví dụ 4. Hai bệnh nhân X và Y bị nhiễm vi rút SARS-CoV-2. Biết rằng xác suất bị biến chứng nặng của bệnh nhân X là 0,1 và của bệnh nhân Y là 0,2. Khả năng bị biến chứng nặng của hai bệnh nhân là độc lập. Hãy tính xác suất của các biến cố:
a) “Cả hai bệnh nhân đều bị biến chứng nặng”;
b) “Cả hai bệnh nhân đều không bị biến chứng nặng”;
c) “Bệnh nhân X bị biến chứng nặng, bệnh nhân Y không bị biến chứng nặng”.
Giải
Gọi A là biến cố “Bệnh nhân X bị biến chứng nặng”. Ta có .
Gọi B là biến cố “Bệnh nhân Y bị biến chứng nặng”. Ta có .
a) Ta thấy A và B là hai biến cố độc lập nên xác suất cả hai bệnh nhân đều bị biến chứng nặng là .
b) Do và độc lập nên xác suất cả hai bệnh nhân đều không bị biến chứng nặng là .
c) Do A và độc lập nên xác suất bệnh nhân X bị biến chứng nặng, bệnh nhân Y không bị biến chứng nặng là .
Ví dụ 5. Số liệu thống kê tại một vùng cho thấy trong các vụ tai nạn ô tô có 0,37% người tử vong, 29% người không thắt dây an toàn và có 0,28% người không thắt dây an toàn và tử vong. Chứng tở rằng việc không thắt dây an toàn khi lái xe và nguy cơ tử vong khi gặp tai nạn có liên quan với nhau.
Lời giải
Chọn ngẫu nhiên một người đã bị tai nạn ô tô.
Gọi A là biến cố “Người đó đã tử vong”. B là biến cố “ Người đó đã không thắt dây an toàn”.
Khi đó, AB là biến cố “ Người đó không thắt dây an toàn và đã tử vong”
Ta có ; .
Suy ra .
Mặt khác .
Vì nên hai biến cố A và B không độc lập.
Vậy việc không thắt dây an toán khi lái xe có liên quan tới nguy cơ tử vong khi gặp tai nạn
II. HỆ THỐNG BÀI TẬP TỰ LUẬN
PHƯƠNG PHÁP
+ Cặp biến cố A và B được gọi là độc lập nếu việc xảy ra hay không xảy ra của biến cố này không ảnh hưởng tới xác suất xảy ra của biến cố kia.
+ Quy tắc nhân xác suất cho hai biến cố độc lập
Nếu hai biến cố A và B độc lập với nhau thì .
Câu 1: Cho hai biến cố A và B là hai biến cố xung khắc với P(A) > 0, P(B) > 0. Chứng tỏ rằng hai biến cố A và B không độc lập.
Lời giải
Hai biến cố A và B xung khắc khi và chỉ khi
Vì P(A) > 0, P(B) > 0nên
Vậy hai biến cố A và B không độc lập.
Câu 2: Có hai túi đựng các viên bị có cùng kích thước và khối lượng. Túi I có 3 viên bi màu xanh và 7 viên bị màu đỏ. Túi II có 10 viên bi màu xanh và 6 viên bi màu đỏ. Từ mỗi túi, lấy ngẫu nhiên ra một viên bị. Tính xác suất để:
a) Hai viên bi được lấy có cùng màu xanh;
b) Hai viên bi được lấy có cùng màu đỏ;
c) Hai viên bi được lấy có cùng màu;
d) Hai viên bi được lấy không cùng màu.
Lời giải
Vì hai túi là khác nhau nên biến cố lấy một viên bi mỗi túi là độc lập.
Gọi biến cố A : "Hai viên bi được lấy có cùng màu xanh", biến cố B : "Hai viên bi được lấy có cùng màu đỏ", biến cố C : "Hai viên bi được lấy có cùng màu"
a) Xác suất lấy được viên bi màu xanh từ túi I là
Xác suất lấy được viên bi màu xanh từ túi II là
Xác suất lấy được hai viên bi cùng màu xanh là
b) Xác suất lấy được viên bi màu đỏ từ túi I là
Xác suất lấy được viên bi màu đỏ từ túi II là
Xác suất lấy được hai viên bi cùng màu đỏ là
c) Ta có mà A và B xung khắc nên
Vậy xác suất để hai viên bi được lấy có cùng màu là .
d) Gọi biến cố D : "Hai viên bi được lấy không cùng màu"
Khi đó
Vậy xác suất để hai viên bi được lấy không cùng màu là .
Câu 3: Có hai túi mỗi túi đựng 10 quả cầu có cùng kích thước và khối lượng được đánh số từ 1 đến 10. Từ mỗi túi, lấy ngẫu nhiên ra một quả. Tính xác suất để trong hai quả cầu được lấy ra không có quả cầu nào ghi số 1 hoặc ghi số 5.
Lời giải
Lấy ngẫu nhiên mỗi túi một quả cầu.
Gọi A là biến cố “Quả cầu được lấy ra từ túi thứ nhất không ghi số 1 hoặc số 5”;
B là biến cố “Quả cầu được lấy ra từ túi thứ hai không ghi số 1 hoặc số 5”.
Khi đó AB là biến cố “Cả hai quả cầu được lấy ra không có quả cầu nào ghi số 1 hoặc 5”.
Ta có
Câu 4: Trong đợt kiểm tra cuối học kì II lớp 11 của các trường trung học phổ thông, thống kê cho thấy có 93% học sinh tỉnh X đạt yêu cầu; 87% học sinh tỉnh Y đạt yêu cầu. Chọn ngẫu nhiên một học sinh của tỉnh X và một học sinh của tỉnh Y. Giả thiết rằng chất lượng học tập của hai tỉnh là độc lập Tính xác suất để:
a) Cả hai học sinh được chọn đều đạt yêu cầu.
b) Cả hai học sinh được chọn đều không đạt yêu cầu.
c) Chỉ có đúng một học sinh được chọn đạt yêu cầu.
d) Có ít nhất một trong hai học sinh được chọn đạt yêu cầu.
Lời giải
Chọn ngẫu nhiên một học sinh của tỉnh X và một học sinh của tỉnh Y.
Gọi A là biến cố “Một học sinh được chọn tỉnh X đạt yêu cầu”;
B là biến cố “Một học sinh được chọn tỉnh Y đạt yêu cầu”.
a) Khi đó AB là biến cố “Cả hai học sinh được chọn đều đạt yêu cầu”.
P(AB) = P(A)P(B) = 0,93.0,87 = 0,8091.
b) là biến cố “Cả hai học sinh được chọn đều không đạt yêu cầu”.
c) là biến cố “Chỉ có đúng một học sinh được chọn đạt yêu cầu”.
= = = = 0,1818.
d) Gọi Dlà biến cố: “Có ít nhất một trong hai học sinh được chọn đạt yêu cầu”
là biến cố: “Cả hai học sinh được chọn đều không đạt yêu cầu”
Câu 5: An và Bình học ở hai nơi khác nhau. Xác suất để An và Bình đạt điểm giỏi về môn Toán trong kỳ thi cuối năm tương ứng là 0,9 và 0,7 . Tính xác suất để cả An và Bình đều đạt điểm giỏi môn Toán.
Lời giải
Gọi A là biến cố “An đạt điểm giỏi về môn Toán”.
Gọi B là biến cố “Bình đạt điểm giỏi về môn Toán”.
Vì hai biến cố A và B độc lập nhau nên xác suất để cả An và Bình đều đạt điểm giỏi môn Toán là: .
Câu 6: Cho A và B là hai biến cố độc lập. Biết P(A) = 0,3 và P(B) = 0,4 . Tính xác suất của biến cố AB .
Lời giải
Ta có: .
................................
................................
................................
Xem thêm Chuyên đề dạy thêm Toán lớp 11 các chương hay khác:
Chuyên đề Đường thẳng và mặt phẳng. Quan hệ song song trong không gian
Chuyên đề Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu ghép nhóm
Tủ sách VIETJACK shopee lớp 10-11 (cả 3 bộ sách):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 11 Global Success
- Giải sgk Tiếng Anh 11 Smart World
- Giải sgk Tiếng Anh 11 Friends Global
- Lớp 11 - Kết nối tri thức
- Soạn văn 11 (hay nhất) - KNTT
- Soạn văn 11 (ngắn nhất) - KNTT
- Giải sgk Toán 11 - KNTT
- Giải sgk Vật Lí 11 - KNTT
- Giải sgk Hóa học 11 - KNTT
- Giải sgk Sinh học 11 - KNTT
- Giải sgk Lịch Sử 11 - KNTT
- Giải sgk Địa Lí 11 - KNTT
- Giải sgk Giáo dục KTPL 11 - KNTT
- Giải sgk Tin học 11 - KNTT
- Giải sgk Công nghệ 11 - KNTT
- Giải sgk Hoạt động trải nghiệm 11 - KNTT
- Giải sgk Giáo dục quốc phòng 11 - KNTT
- Giải sgk Âm nhạc 11 - KNTT
- Lớp 11 - Chân trời sáng tạo
- Soạn văn 11 (hay nhất) - CTST
- Soạn văn 11 (ngắn nhất) - CTST
- Giải sgk Toán 11 - CTST
- Giải sgk Vật Lí 11 - CTST
- Giải sgk Hóa học 11 - CTST
- Giải sgk Sinh học 11 - CTST
- Giải sgk Lịch Sử 11 - CTST
- Giải sgk Địa Lí 11 - CTST
- Giải sgk Giáo dục KTPL 11 - CTST
- Giải sgk Hoạt động trải nghiệm 11 - CTST
- Giải sgk Âm nhạc 11 - CTST
- Lớp 11 - Cánh diều
- Soạn văn 11 Cánh diều (hay nhất)
- Soạn văn 11 Cánh diều (ngắn nhất)
- Giải sgk Toán 11 - Cánh diều
- Giải sgk Vật Lí 11 - Cánh diều
- Giải sgk Hóa học 11 - Cánh diều
- Giải sgk Sinh học 11 - Cánh diều
- Giải sgk Lịch Sử 11 - Cánh diều
- Giải sgk Địa Lí 11 - Cánh diều
- Giải sgk Giáo dục KTPL 11 - Cánh diều
- Giải sgk Tin học 11 - Cánh diều
- Giải sgk Công nghệ 11 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 11 - Cánh diều
- Giải sgk Giáo dục quốc phòng 11 - Cánh diều
- Giải sgk Âm nhạc 11 - Cánh diều



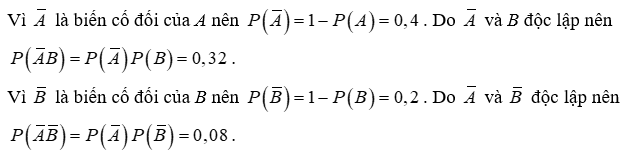



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

