Tổng hợp bài tập Chương 2 phần Hình học Toán 6 có đáp án

Bài viết Tổng hợp bài tập Chương 2 phần Hình học lớp 6 với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập Chương 2 phần Hình học.

Tổng hợp bài tập Chương 2 phần Hình học Toán 6 có đáp án

Câu 1: Chọn câu sai:

A. Góc là hình gồm hai tia chung gốc

B. Hai tia chung gốc tạo thành góc bẹt

C. Hai góc bằng nhau có số đo bằng nhau

D. Hai góc có số đo bằng nhau thì bằng nhau

Lời giải:

Ta có:

    + Góc là hình gồm hai tia chung gốc nên A đúng.

    + Góc bẹt là góc có hai cạnh là hai tia đối nhau nên B sai vì hai tia chung gốc chưa chắc đã đối nhau.

    + Hai góc bằng nhau có số đo bằng nhau nên C đúng.

    + Hai góc có số đo bằng nhau thì bằng nhau nên D đúng.

Chọn đáp án B.

Câu 2: Chọn câu sai:

A. Góc vuông là góc có số đo bằng 90°

B. Góc có số đo lớn hơn 0° và nhỏ hơn 90° là góc nhọn

C. Góc tù là góc có số đo lớn hơn 90° và nhỏ hơn 180°

D. Góc có số đo nhỏ hơn 180° là góc tù

Lời giải:

Ta có góc vuông là góc có số đo bằng 90°; góc có số đo lớn hơn 0° và nhỏ hơn 90° là góc nhọn và góc tù là góc có số đo lớn hơn 90° và nhỏ hơn 180° nên A, B, C đều đúng.

Góc có số đo nhỏ hơn 180° là góc tù là sai vì góc nhọn, góc vuông đều có số đo nhỏ hơn 180°

Chọn đáp án D.

Câu 3: Chọn phát biểu đúng:

A. Góc có số đo 120° là góc vuông     B. Góc có số đo 80° là góc tù

C. Góc có số đo 100° là góc nhọn     D. Góc có số đo 150° là góc tù

Lời giải:

    + Góc có số đo 120° là góc tù vì 90° < 120° < 180° nên A sai.

    + Góc có số đo 80° là góc nhọn vì 0° < 80° < 90° nên B sai.

    + Góc có số đo 100° là góc tù vì 90° < 100° < 180° nên C sai.

    + Góc có số đo 150°là góc tù vì 90° < 150° < 180° nên D đúng.

Chọn đáp án D.

Câu 4: Cho 9 tia chung gốc (không có tia nào trùng nhau) thì số góc tạo thành là:

A. 16     B. 72     C. 36     D. 42

Lời giải:

Số góc tạo thành là 9.(9 - 1)/2 = 36 góc

Chọn đáp án C.

Câu 5: Góc trên hình có số đo bao nhiêu độ:

A. 50°     B. 40°     C. 60°     D. 130°

Lời giải:

Góc trên hình có số đo 50°

Chọn đáp án A.

Câu 6: Cho hình vẽ sau:

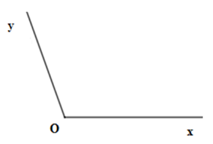
Chọn câu đúng:

A. ∠xOy , đỉnh O, cạnh Ox và Oy     B. ∠xyO , đỉnh O, cạnh Ox và Oy

C. ∠Oxy , đỉnh O, cạnh Ox và Oy     D. ∠xOy , đỉnh y, cạnh Ox và Oy

Lời giải:

Góc trên hình là ∠xOy, đỉnh O, cạnh Ox và Oy.

Chọn đáp án A.

Câu 7: Kể tên các góc có trên hình vẽ:

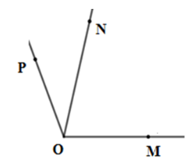
Lời giải:

Các góc tạo thành là: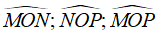

Chọn đáp án B.

Câu 8: Kể tên tất cả các góc có một cạnh là Om có trên hình vẽ sau:

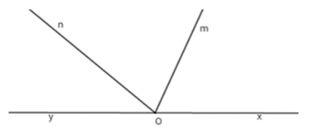
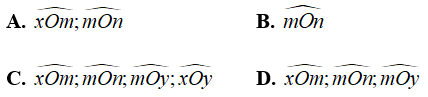
Lời giải:

Các góc cần tìm là: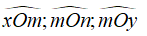

Chọn đáp án D.

Câu 9: Cho ∠xOm = 45° và góc xOm bằng góc yAn. Khi đó góc yAn bằng:

A. 50°     B. 40°     C. 45°     D. 30°

Lời giải:

Vì ∠xOm = ∠yAn mà ∠xOm = 45° nên ∠yAn = 45°

Chọn đáp án C.

Câu 10: Cho các góc sau: ∠A = 30°; ∠B = 60°; ∠C = 110°; ∠D = 90°. Chọn câu sai:

A. ∠B < ∠D     B. ∠C <∠D     C. ∠A < ∠B     D. ∠B < ∠C

Lời giải:

Ta có:

    + ∠B < ∠D (60° < 90°) nên A đúng.

    + ∠C > ∠D (110° > 90°) nên B sai.

    + ∠A < ∠B (30° < 60°) nên C đúng.

    + ∠B < ∠C (60° < 110°) nên D đúng.

Chọn đáp án B.

Câu 11: Chọn phát biểu đúng trong các phát biểu sau:

A. Hai góc tù là hai góc kề nhau

B. Cho ba tia chung gốc Ox, Oy, Oz, ta luôn có: ∠xOy + ∠yOz = ∠xOz

C. Nếu tia Oy nằm giữa hai tia On và Om thì khi đó ta có: ∠yOn + ∠yOm = ∠mOn

D. Nếu ∠A và ∠B là hai góc bù nhau thì ∠A + ∠B = 90°

Lời giải:

    + Nếu tia Oy nằm giữa hai tia On và Om thì khi đó ta có: ∠yOn + ∠yOm = ∠mOn nên C đúng.

    + Nếu ∠A và ∠B là hai góc bù nhau thì ∠A + ∠B = 180° nên D sai.

    + Hai góc kề nhau là hai góc có một cạnh chung và hai cạnh còn lại nằm trên hai nửa mặt phẳng đối nhau có bờ là đường thẳng chứa cạnh chung nên hai góc tù chưa chắc kề nhau, suy ra A sai.

    + Cho ba tia chung gốc Ox, Oy, Oz, ta luôn có: ∠xOy + ∠yOz = ∠xOz là sai vì thiếu điều kiện Oy nằm giữa Ox và Oz. Suy ra B sai.

Chọn đáp án C.

Câu 12: Chọn câu sai trong các câu sau:

A. Nếu tia Ot nằm giữa hai tia Ou và Ov thì ∠tOu + ∠tOv = ∠uOv

B. Nếu hai góc có một cạnh chung và hai cạnh còn lại nằm trên hai nửa mặt phẳng đối nhau bờ là đường thẳng chứa cạnh chung thì hai góc đó kề nhau

C. Hai góc vừa kề nhau, vừa bù nhau gọi là hai góc phụ nhau

D. Hai góc kề bù có tổng là 180°

Lời giải:

Các đáp án A, B, D đúng.

C sai vì hai góc vừa kề nhau, vừa bù nhau là hai góc kề bù.

Chọn đáp án C.

Câu 13: Trên cùng một nửa mặt phẳng bờ là tia Ox có ∠xOy = 30°, ∠xOz = 65°, chọn phát biểu đúng trong các phát biểu sau:

A. Tia Ox nằm giữa hai tia Oy và Oz

B. Tia Oy nằm giữa hai tia Oz và Ox

C. Tia Oz nằm giữa hai tia Oy và Ox

D. Chưa thể kết luận được tia nào nằm giữa hai tia còn lại

Lời giải:

Vì ∠xOy = 30°, ∠xOz = 65°, suy ra ∠xOy < ∠xOz (30° < 65°) nên tia Oy nằm giữa hai tia Oz và Ox

Chọn đáp án B.

Câu 14: Cho ∠xOy và ∠yOy' là hai góc kề bù. Biết ∠xOy = 80°, số đo của ∠yOy' là:

A. 100°     B. 70°     C. 80°     D. 60°

Lời giải:

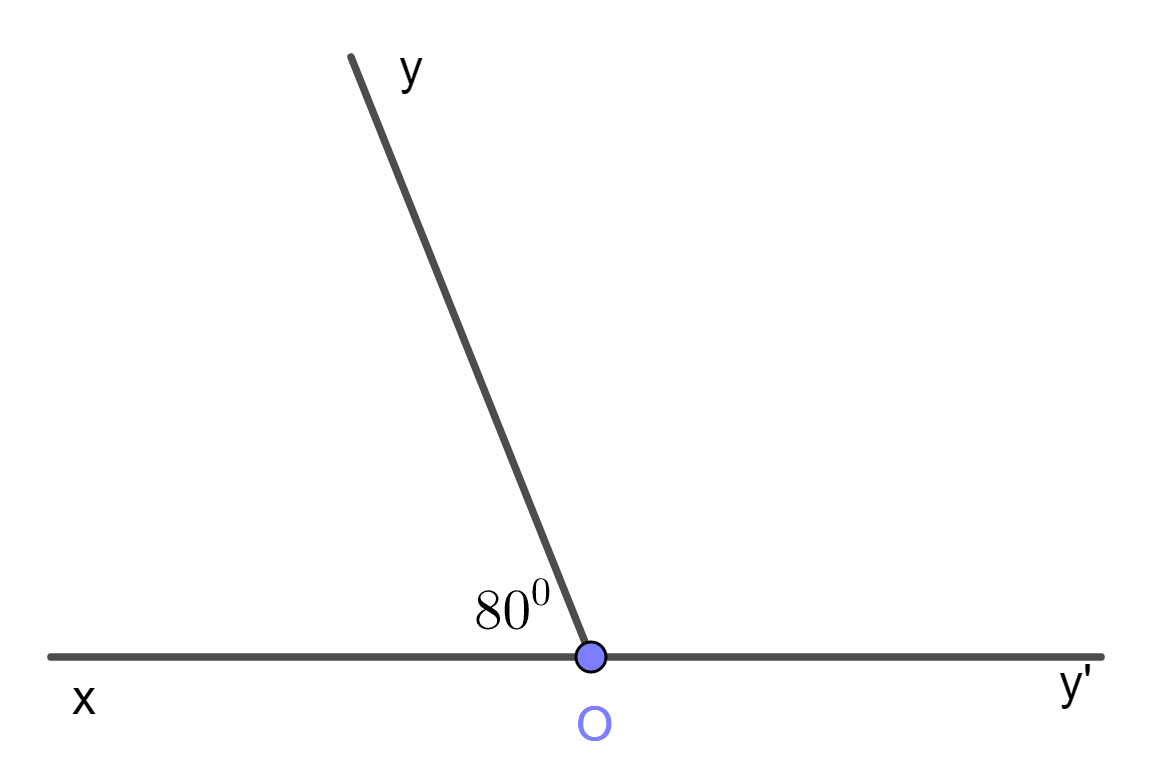
Vì ∠xOy và ∠yOy' là hai góc kề bù nên ta có: ∠xOy + ∠yOy' = 180° ⇒ ∠yOy' = 180° - 80° = 100°

Chọn đáp án A.

Câu 15: Cho hình vẽ:

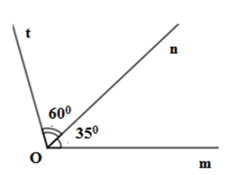
Số đo của ∠tOm là:

A. 105°     B. 100°     C. 115°     D. 95°

Lời giải:

Vì tia On nằm giữa hai tia Om và Ot ⇒ ∠tOn + ∠nOm = ∠tOm ⇒ ∠tOm = 60° + 35° = 95°

Chọn đáp án D.

Câu 16: Cho ∠AOB = 120°, vẽ tia OC sao cho tia OB nằm giữa hai tia OA và OC đồng thời ∠COB = 50°. Tính số đo ∠AOC

A. 70°     B. 170°     C. 65°     D. 60°

Lời giải:

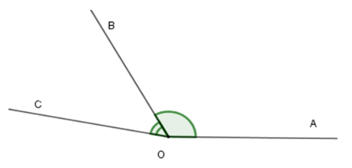
Vì tia OB nằm giữa hai tia OA và OC nên ∠AOB + ∠BOC = ∠AOC

Suy ra ∠AOC = 120° + 50° = 170°.

Chọn đáp án B.

Câu 17: Tính góc yOz trong hình vẽ sau:

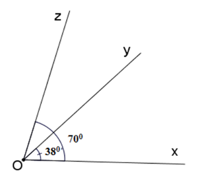
A. 32°     B. 70°     C. 38°     D. 60°

Lời giải:

Vì hai tia Oy, Oz cùng thuộc nửa mặt phẳng bờ là đường thẳng chứa tia Ox

Lại có ∠xOy < ∠xOz (38° < 70°) nên tia Oy nằm giữa hai tia Ox và Oz

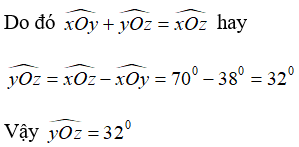
Chọn đáp án A.

Câu 18: Cho ∠A và ∠B là hai góc phụ nhau và chúng có số đo bằng nhau. Tính số đo mỗi góc:

A. ∠A = 30°; ∠B = 60°     B. ∠A = ∠B = 40°     C. ∠A = ∠B = 45°     D. ∠A = 50°; ∠B = 45°

Lời giải:

Vì ∠A và ∠B là hai góc phụ nhau nên ∠A + ∠B = 90° mà ∠A = ∠B

Nên ta có ∠A + ∠A = 90° hay 2.∠A = 90° suy ra ∠B = ∠A = 90° : 2 = 45°

Chọn đáp án C.

Câu 19: Cho ba tia chung gốc Ox; Oy; Oz thỏa mãn ∠xOy = 130°; ∠yOz = 120°; ∠zOx = 110°. Chọn câu đúng:

A. Tia nằm giữa hai tia và

B. Tia nằm giữa hai tia và

C. Không có tia nào nằm giữa hai tia còn lại

D. Tia nằm giữa hai tia và

Lời giải:

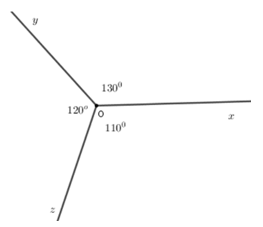
Ta có ∠xOy + ∠yOz > ∠xOz (do 130° + 120° > 110° ) nên tia Oy không nằm giữa hai tia Oz và Ox

Lại có ∠xOy + ∠xOz > ∠yOz (do 130° + 110° > 120° ) nên tia Ox không nằm giữa hai tia Oy và Oz

Lại có ∠zOy + ∠xOz > ∠xOy (do 120° + 110° > 130° ) nên tia Oz không nằm giữa hai tia Oy và Ox

Vậy không có tia nào nằm giữa hai tia còn lại.

Chọn đáp án C.

Câu 20: Cho hình vẽ sau với và là hai tia đối nhau. Chọn câu sai:

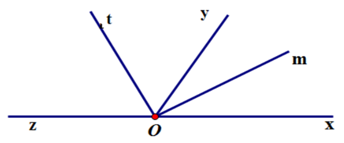
A. Hai góc ∠mOx; ∠mOz là hai góc kề bù

B. Hai góc ∠xOy; ∠tOz là hai góc kề nhau

C. Hai góc ∠tOy; ∠yOx là hai góc kề nhau

D. Hai góc ∠tOz; ∠tOx là hai góc kề bù

Lời giải:

    + Hai góc ∠mOx; ∠mOz là hai góc kề bù nên A đúng.

    + Hai góc ∠xOy; ∠tOz là hai góc không kề nhau nên B sai.

    + Hai góc ∠tOy; ∠yOx là hai góc kề nhau nên C đúng.

    + Hai góc ∠tOz; ∠tOx là hai góc kề bù nên D đúng.

Chọn đáp án B.

Câu 21: Chọn phát biểu sai trong các phát biểu sau:

A. Nếu tia Ot là tia phân giác của ∠xOy thì tia Ot nằm giữa hai tia Ox, Oy

B. Nếu tia Ot là tia phân giác của ∠xOy thì ∠xOt = ∠yOt = ∠xOy/2

C. Nếu ∠xOt = ∠yOt thì tia Ot là tia phân giác của ∠xOy

D. Nếu ∠xOt = ∠yOt và tia Ot nằm giữa hai tia Ox, Oy thì tia Ot là tia phân giác của ∠xOy

Lời giải:

Nếu ∠xOt = ∠yOt và tia Ot nằm giữa hai tia Ox, Oy thì tia Ot là tia phân giác của ∠xOy nên C sai, D đúng

Chọn đáp án C.

Câu 22: Cho Ot là phân giác của ∠xOy. Biết ∠xOy = 100°, số đo của ∠xOt là:

A. 40°     B. 60°     C. 50°     D. 200°

Lời giải:

Vì Ot là phân giác của ∠xOy thì

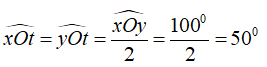
Chọn đáp án C.

Câu 23: Cho ∠xOy là góc vuông có tia On là phân giác, số đo của ∠xOn là:

A. 40°     B. 90°     C. 45°     D. 85°

Lời giải:

Vì On là tia phân giác của ∠xOy nên

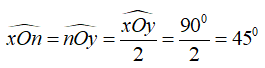
Chọn đáp án C.

Câu 24: Cho tia On là tia phân giác của ∠mOt. Biết ∠mOn = 70°, số đo của ∠mOt là:

A. 140°     B. 120°     C. 35°     D. 60°

Lời giải:

Vì tia On là tia phân giác của ∠mOt nên

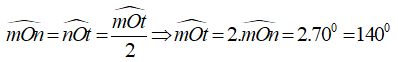
Chọn đáp án A.

Câu 25: Cho ∠AOB = 90° và tia OB là tia phân giác của góc AOC . Khi đó góc AOC là:

A. Góc vuông     B. Góc nhọn     C. Góc tù     D. Góc bẹt

Lời giải:

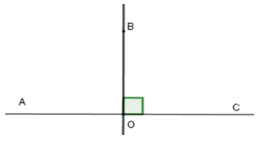
Vì tia là tia phân giác của góc nên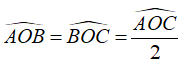

Do đó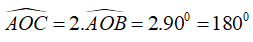

Nên góc AOC là góc bẹt.

Chọn đáp án D.

Câu 26: Cho ∠AOC = 60°. Vẽ tia OB sao cho OA là tia phân giác của ∠BOC . Tính số đo của ∠AOB và ∠BOC

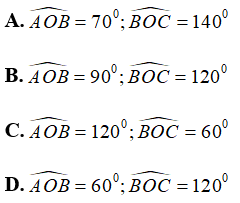
Lời giải:

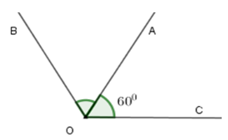
Vì OA là tia phân giác của ∠BOC nên ta có:

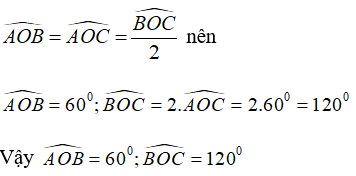
Chọn đáp án D.

Câu 27: Cho ∠AOB = 110° và ∠AOC = 55° sao cho ∠AOB và ∠AOC không kề nhau. Chọn câu sai:

A. Tia OC nằm giữa hai tia OA và OB

B. Tia OC là tia phân giác góc AOB

C. ∠BOC = 65°

D. ∠BOC = 55°

Lời giải:

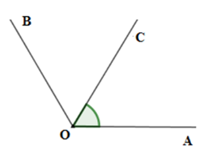
Vì ∠AOB và ∠AOC không kề nhau nên hai tia OC; OB thuộc cùng nửa mặt phẳng bở là đường thẳng chứa tia OA.

Lại có: ∠AOC < ∠AOB (55° < 110°) nên tia OC nằm giữa hai tia OA và OB . (1)

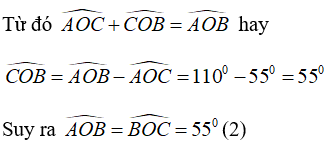
Từ (1) và (2) suy ra tia OC là tia phân giác góc AOB.

Vậy A, B, D đúng và C sai.

Chọn đáp án C.

Câu 28: Cho ∠xOy và ∠yOz là hai góc kề bù. Biết ∠xOy = 120° và tia Ot là tia phân giác của ∠yOz. Tính số đo góc xOt.

A. 140°     B. 150°     C. 90°     D. 120°

Lời giải:

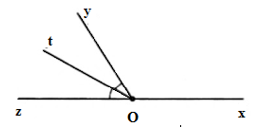
Vì ∠xOy và ∠yOz là hai góc kề bù nên ∠xOy + ∠yOz = 180° mà ∠xOy = 120° nên ∠yOz = 180° - 120° = 60°

Lại có tia Ot là tia phân giác của ∠yOz nên

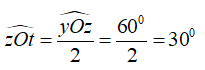
Lại có ∠zOt; ∠tOx là hai góc kề bù nên

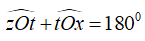
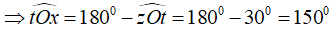
Vậy ∠tOx = 150°

Chọn đáp án B.

Câu 29: Cho góc AOB và tia phân giác OC của góc đó. Vẽ tia phân giác OM của góc BOC . Biết ∠BOM = 35°. Tính số đo góc AOB

A. 150°     B. 120°     C. 140°     D. 160°

Lời giải:

Vì tia OM là tia phân giác góc BOC nên ∠BOC = 2.∠BOM = 2.35° = 70°

Lại có tia Oc là tia phân giác góc AOB nên ∠AOB = 2.∠BOC = 2.70° = 140°

Vậy ∠AOB = 140°

Chọn đáp án C.

Câu 30: Cho góc bẹt ∠xOy. Trên cùng một nửa mặt phẳng bờ xy vẽ các tia Om, On sao cho ∠xOm = a° (a < 180) và ∠yOn = 70°. Với giá trị nào a của thì tia On là tia phân giác của ∠yOm

A. 45°     B. 30°     C. 50°     D. 40°

Lời giải:

Vì tia On là tia phân giác của ∠yOm nên ∠yOm = 2.∠yOn = 2.70° = 140°

Lại có xOy là góc bẹt nên ∠xOm và ∠yOm là hai góc kề bù

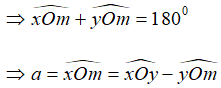
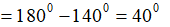
Vậy a = 40°

Chọn đáp án D.

Câu 31: Chọn phát biểu đúng trong các phát biểu sau:

A. Đường tròn tâm O, bán kính R là hình gồm các điểm cách O một khoảng bằng R, kí hiệu là (O; R).

B. Đường tròn tâm O, đường kính R là hình gồm các điểm cách O một khoảng bằng R, kí hiệu là (O; R).

C. Đường tròn tâm O, bán kính R là hình gồm các điểm cách O một khoảng bằng R/2, kí hiệu là (O; R).

D. Hình tròn tâm O, bán kính R là hình gồm các điểm cách O một khoảng bằng R, kí hiệu là (O; R).

Lời giải:

Đường tròn tâm O, bán kính R là hình gồm các điểm cách O một khoảng bằng R , kí hiệu là (O; R) nên A đúng, C sai.

Đường tròn tâm O đường kính R có bán kính R/2 nên là tập hợp các điểm cách O một khoảng R/2 . Đáp án B sai

Hình tròn là hình gồm các điểm nằm trên đường tròn và các điểm nằm bên trong đường tròn đó. Đáp án D sai

Chọn đáp án A.

Câu 32: Chọn phát biểu sai trong các phát biểu sau:

A. Hình gồm các điểm nằm trên đường tròn và các điểm nằm trong đường tròn đó là hình tròn.

B. Dây cung không đi qua tâm là bán kính của đường tròn đó.

C. Hai điểm A và B của một đường tròn chia đường tròn đó thành hai cung. Đoạn thẳng nối hai mút của một cung là dây.

D. Dây cung đi qua tâm là đường kính của đường tròn đó.

Lời giải:

Ta thấy A, C, D đúng.

B sai vì dây cung không thể là bán kính của đường tròn (theo định nghĩa dây cung)

Chọn đáp án B.

Câu 33: Nếu điểm M nằm trong đường tròn tâm O bán kính 4cm. Khi đó:

A. OM < 4cm     B. OM = 4cm     C. OM > 4cm     D. OM ≥ 4cm

Lời giải:

Vì điểm M nằm trong đường tròn tâm O bán kính 4cm nên OM < 4cm.

Chọn đáp án A.

Câu 34: Cho đường tròn (O; 5cm) và OM = 6cm. Chọn câu đúng:

A. Điểm M nằm trên đường tròn     B. Điểm M nằm trong đường tròn

C. Điểm M nằm ngoài đường tròn     D. Điểm M trùng với tâm đường tròn

Lời giải:

Ta thấy OM > R (6cm > 5cm) nên điểm M nằm ngoài đường tròn (O; R)

Chọn đáp án C.

Câu 35: Cho đường tròn (M; 1,5cm) và ba điểm A, B, C sao cho OA = 1cm; OB = 1,5cm; OC = 2cm. Chọn câu đúng:

A. Điểm A nằm trên đường tròn, điểm B nằm trong đường tròn và điểm C nằm ngoài đường tròn (M; 1,5cm)

B. Điểm A và điểm C nằm ngoài đường tròn, điểm B nằm trên đường tròn (M; 1,5cm)

C. Điểm A nằm trong đường tròn, điểm B nằm trên đường tròn và điểm C nằm ngoài đường tròn (M; 1,5cm)

D. Cả ba đều nằm trên đường tròn (M; 1,5cm)

Lời giải:

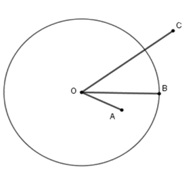
Đường tròn (M; 1,5cm) có tâm M và bán kính R = 1,5cm

Ta thấy:

    + OA < R (1cm < 1,5cm) nên điểm A nằm trong đường tròn (M; 1,5cm)

    + OB = R (1,5cm = 1,5cm) nên điểm B nằm trên (thuộc) đường tròn (M; 1,5cm)

    + OC > R (2cm > 1,5cm) nên điểm C nằm ngoài đường tròn (M; 1,5cm)

Chọn đáp án C.

Câu 36: Cho hình vẽ sau:

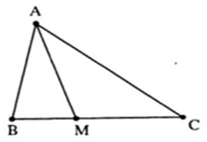
Kể tên các góc trong tam giác ABM:

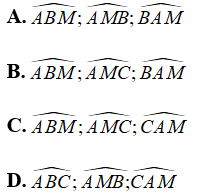
Lời giải:

Các góc trong tam giác ABM là: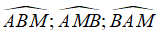

Chọn đáp án A.

Câu 37: Cho hình vẽ sau:

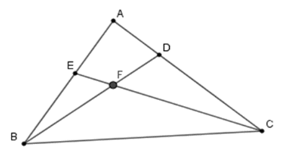
Kể tên các tam giác có chung cạnh BC:

A. ΔFBC; ΔEBC; ΔABC     B. ΔEBC; ΔDBC; ΔABC

C. ΔFBC; ΔEBC; ΔDBC     D. ΔFBC; ΔEBC; ΔDBC; ΔABC

Lời giải:

Các tam giác có chung cạnh trong hình vẽ là: ΔFBC; ΔEBC; ΔDBC; ΔABC

Chọn đáp án D.

Câu 38: Cho hình vẽ sau:

Có bao nhiêu cặp tam giác mà có một góc của tam giác này kề bù với một góc của tam giác kia:

A. 1     B. 2     C. 4     D. 3

Lời giải:

Ta thấy trên hình vẽ có các cặp góc kề bù mà mỗi góc thuộc một tam giác là: ∠EFB và ∠CFB; ∠BFC và ∠CFD; ∠BEC và ∠AEC; ∠BDC và ∠BDA

Như vậy ta có bốn cặp tam giác thỏa mãn điểu kiện là: ΔBEF và ΔBFC; ΔDFC và ΔBFC; ΔBEC và ΔAEC; ΔBDC và ΔBDA

Chọn đáp án C.

Câu 39: Cho hình vẽ dưới đây:

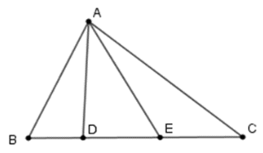
Góc AEB là góc chung của những tam giác nào:

A. ΔAEB; ΔABD     B. ΔAEB; ΔAED

C. ΔAEB; ΔABC     D. ΔAEB; ΔAEC

Lời giải:

Ta có các tam giác có chứa góc AEB là: ΔAEB; ΔAED

Chọn đáp án B.

Câu 40: Cho hình vẽ dưới đây:

Có bao nhiêu tam giác có một cạnh AD trên hình vẽ:

A. 4     B. 1     C. 2     D. 3

Lời giải:

Các tam giác có một cạnh AD trên hình vẽ là: ABD; ADE; ADC

Chọn đáp án D.

Xem thêm các phần lý thuyết, các dạng bài tập Toán lớp 6 có đáp án chi tiết hay khác:

• Bài tập Tia phân giác của góc
• Lý thuyết Đường tròn
• Bài tập Đường tròn
• Lý thuyết Tam giác
• Bài tập Tam giác

Xem thêm các loạt bài Để học tốt Toán lớp 6 hay khác:

• Giải bài tập sgk Toán 6
• Giải sách bài tập Toán 6
• Top 52 Đề thi Toán 6 có đáp án

---