10 Bài tập Sự tương giao giữa đường thẳng và parabol nâng cao (có lời giải)
Tài liệu Bài tập Sự tương giao giữa đường thẳng và parabol nâng cao lớp 9 có lời giải với các dạng bài tập cơ bản, nâng cao đầy đủ các mức độ: nhận biết, thông hiểu, vận dụng, vận dụng cao sẽ giúp học sinh ôn luyện và biết cách làm bài tập Toán 9.
10 Bài tập Sự tương giao giữa đường thẳng và parabol nâng cao (có lời giải)
(199k) Xem Khóa học Toán 9 KNTTXem Khóa học Toán 9 CDXem Khóa học Toán 9 CTST
Câu 1: Tìm phương trình đường thẳng (d) đi qua điểm I (0; 1) và cắt parabol (P): y = x2 tại hai điểm phân biệt M và N sao cho
A. y = 2x + 1; y = −2x – 1
B. y = 2x + 1; y = −2x + 1
C. y = 2x + 1; y = 2x – 1
D. y = −2x + 2; y = −2x + 1
Lời giải:
Đường thẳng (d) qua I với hệ số góc a có dạng: y = ax + 1
Phương trình hoành độ giao điểm của (d) và (P) là x2 = ax + 1 ⇔ x2 − ax – 1 = 0 (1)
Vì ∆ = a2 + 4 > 0 với mọi a, (1) luôn có hai nghiệm phân biệt nên (d) luôn cắt (P) tại hai điểm phân biệt M (x1; y1), N (x2; y2) hay M (x1; ax1 + 1), N (x2; ax2 + 1)
Vậy phương trình đường thẳng cần tìm là y = 2x + 1; y = −2x + 1
Đáp án cần chọn là: B
Câu 2: Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình 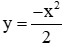
A. Vuông tại H
B. Vuông tại K
C. Vuông tại I
D. Đều
Lời giải:
Đường thẳng (d): y = kx – 2
Xét phương trình
Ta có: ∆ = k2 + 4 > 0 với mọi k; suy ra (1) có hai nghiệm phân biệt
Vậy (d) luôn cắt (P) tại hai điểm phân biệt.
Giả sử (1) có hai nghiệm phân biệt x1; x2
Suy ra A (x1; y1), B (x2; y2) thì H (x1; 0), K (x2; 0)
Khi đó IH2 = x12 + 4, IK2 = x22 + 4, HK2 = (x1 – x2)2
Theo định lý Vi-ét thì x1x2 = −4 nên IH2 + IK2 = x12 + x22 + 8 = KH2
Vậy tam giác IHK vuông tại I
Đáp án cần chọn là: C
Câu 3: Cho Parabol (P): y = x2 và đường thẳng (d): y = mx + 4.
Biết đường thẳng (d) luôn cắt đồ thị (P) tại hai điểm phân biệt A, B.
Gọi x1; x2 là hoành độ của các điểm A, B.
Tìm giá trị lớn nhất của
Lời giải:
Phương trình hoành độ giao điểm của (d) và (P) là: x2 = mx + 4 ⇔ x2 − mx − 4 = 0. Ta có ∆ = m2 + 16 > 0, với mọi m nên phương trình luôn có 2 nghiệm phân biệt, suy ra đường thẳng (d) luôn cắt (P) tại hai điểm phân biệt.
Dấu “=” xảy ra khi m2 + 8 = 2m + 7 ⇔ (m – 1)2 = 0 ⇔ m = 1
Suy ra giá trị lớn nhất của Q là 1 khi m = 1
Đáp án cần chọn là: C
Câu 4: Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d): 2x – y – a2 = 0 và parabol (P): y = ax2 (a > 0). Tìm a để (d) cắt (P) tại hai điểm phân biệt A, B. Khi đó có kết luận gì về vị trí của hai điểm A, B
A. Với 0 < a < 1 thì (d) cắt (P) tại hai điểm phân biệt A, B và A, B nằm ở bên phải trục Oy
B. Với a > 0 thì (d) cắt (P) tại hai điểm phân biệt A, B và A, B nằm ở bên phải trục Oy
C. Với 0 < a < 1 thì (d) cắt (P) tại hai điểm phân biệt A, B và A, B nằm ở bên trái trục Oy
D. Với 0 < a < 1 thì (d) cắt (P) tại hai điểm phân biệt A, B và A, B nằm ở hai phía với trục Oy
Lời giải:
Ta có (d): 2x – y – a2 = 0 ⇔ y = 2x − a2
Xét phương trình ax2 = 2x – a2 ax2 – 2x + a2 = 0 (1) ⇔ ∆' > 0 ⇔ a < 1
Kết hợp với điều kiện a > 0 ta có 0 < a < 1 khi đó (1)
có hai nghiệm xA; xB (xA; xB là hoành độ của A và B) thỏa mãn 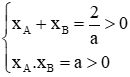
Đáp án cần chọn là: A
Vận dụng cao: Gọi là hoành độ của A và B. Tìm giá trị nhỏ nhất của biểu thức
Lời giải:
Theo câu trước ta có xA; xB là hai nghiệm của phương trình ax2 – 2x + a2 = 0
Theo định lý Vi-ét ta có:
Ta có: 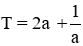
Đáp án cần chọn là: C
Câu 5: Cho parabol (P): y = x2 và đường thẳng (d): y = mx + 1. Gọi A (x1; y1) và B (x2; y2) là các giao điểm của (d) và (P). Tìm m để biểu thức M = (y1 − 1)( y2 − 1) đạt giá trị lớn nhất.
A. m = 0
B. m = 2
C. m = 1
D. m = −1
Lời giải:
Phương trình hoành độ giao điểm của đường thẳng và Parabol là:
x2 = mx + 1 ⇔ x2 – mx – 1 = 0 (1)
∆ = m2 + 4 > 0 với mọi m nên 91) có hai nghiệm phân biệt, suy ra (d) luôn cắt (P) tại hai điểm phân biệt A (x1; y1) và B (x2; y2) với x1; x2 là hai nghiệm của phương trình (1).
Theo định lý Vi-ét, ta có: x1 + x2 = m; x1.x2 = −1
Vì A; B ∈(P) ⇒ y1 = x12; y2 = x22
Ta có
M = (y1 − 1)(y2 − 1) = (x12− 1) (x22 − 1) = x12. x22 – (x12 + x22) + 1
= x12. x22 + x12. x22 − (x1 + x2)2 + 1 = 1 – 2 − m2 + 1 = −m2 ≤ 0
Vậy MaxM = 0 khi m = 0
Đáp án cần chọn là: A
Câu 6: Trong mặt phẳng tọa độ Oxy cho Parabol (P): y = x2 và đường thẳng (d): 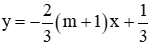
Lời giải:
Xét phương trình hoành độ giao điểm của (d) và (P) ta có:
Ta thấy phương trình (1) có hệ số a và c trái dấu nên luôn có hai nghiệm phân biệt mọi m nên (P) và (d) luôn cắt nhau tại hai điểm phân biệt với mọi m
Vì f(x) = x3 + (m + 1)x2 – x nên ta có:
f(x1) − f(x2) = x13 – x23 + (m + 1)(x12 – x22) − x1 + x2
⇒ 2(f(x1) − f(x2)) = 2x13 – 2x23 − 3(x1 + x2)(x12 – x22) − 2x1 + 2x2
= −x13 + x23 + 3x1.x2 (x2 – x1) – 2(x1 − x2) = −x13 + x23 + (x1 − x2) – 2(x1 − x2)
= −(x13 − x23 − 3x1.x2 (x1 – x2)) = [(x1 − x2)( x12 + x22 − 2 x1.x2)] = (x1 − x2)3
Đáp án cần chọn là: D
Câu 7: Trong mặt phẳng Oxy cho đường thẳng 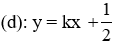
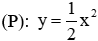
Lời giải:
Xét phương trình hoành độ giao điểm của (d) và (P):
⇔ x2 – 2hx – 1 = 0 (*). Nhận thấy a = 1; c = −1 trái dấu nhau nên phương trình (*) luôn có hai nghiệm phân biệt hay đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt A và B với mọi k
Gọi A(xA; yA); B(xB; yB) thì xA; xB là hai nghiệm của phương trình (*) và
Đáp án cần chọn là: A
Câu 8: Trên parabol (P): y = x2 ta lấy ba điểm phân biệt A (a; a2); B (b; b2); C (c; c2) thỏa mãn a2 – b = b2 – c = c2 – a. Hãy tính tích T = (a + b + 1)(b + c + 1)(c + a + 1)
A. T = 2
B. T = 1
C. T = −1
D. T = 0
Lời giải:
Đáp án cần chọn là: C
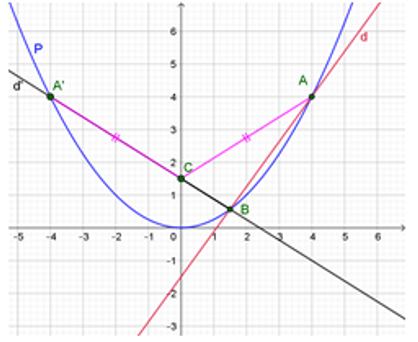
Câu 9: Cho parabol 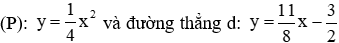
Lời giải:
Hoành độ của A và B là nghiệm của phương trình
Dễ thấy hai điểm A, B cùng nằm về một phía so với trục tung (do cùng có hoành độ dương).
Lấy điểm A’ (− 4; 4) đối xứng với A qua trục tung
Khi đó CA + CB = CA’ + CB ≥ A’B, nên CA + CB đạt giá trị nhỏ nhất khi và chỉ khi A’, C, B thẳng hàng, tức là khi C là giao điểm của đường thẳng A’B với trục tung.
Phương trình đường thẳng d’ đi qua A’ và B có dạng y = ax + b
Suy ra giao điểm (d’) với trục tung có hoành độ
Đáp án cần chọn là: B
Câu 10: Trong mặt phẳng Oxy, cho parabol (P): 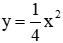
A. C(2; 1)
B. C(1; 2)
C. C(1; 0)
D. C(0; 2)
Lời giải:
Vậy 2 giao điểm A (6; 9), B (−4; 4)
Gọi 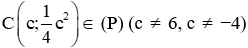
Tam giác ABC vuông tại C khi và chỉ khi AB2 = AC2 + BC2
Vậy C (2; 1) là điểm thỏa mãn đề bài
Đáp án cần chọn là: A
(199k) Xem Khóa học Toán 9 KNTTXem Khóa học Toán 9 CDXem Khóa học Toán 9 CTST
Xem thêm bài tập trắc nghiệm Toán lớp 9 có lời giải hay khác:
- Bài tập Giải bài toán bằng cách lập phương trình, hệ phương trình nâng cao (có đáp án)
- Bài tập Hệ thức Vi-ét và ứng dụng nâng cao (có lời giải)
- 40 Bài tập Hàm số y = ax^2; Phương trình bậc hai một ẩn nâng cao (có đáp án)
- Top 20 Bài tập trắc nghiệm Hàm số y = ax^2; Phương trình bậc hai một ẩn (có đáp án)
Tủ sách VIETJACK luyện thi vào 10 cho 2k11 (2026):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Loạt bài Chuyên đề: Lý thuyết - Bài tập Toán lớp 9 Đại số và Hình học có đáp án có đầy đủ Lý thuyết và các dạng bài được biên soạn bám sát nội dung chương trình sgk Đại số 9 và Hình học 9.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 9 Global Success
- Giải sgk Tiếng Anh 9 Smart World
- Giải sgk Tiếng Anh 9 Friends plus
- Lớp 9 Kết nối tri thức
- Soạn văn 9 (hay nhất) - KNTT
- Soạn văn 9 (ngắn nhất) - KNTT
- Giải sgk Toán 9 - KNTT
- Giải sgk Khoa học tự nhiên 9 - KNTT
- Giải sgk Lịch Sử 9 - KNTT
- Giải sgk Địa Lí 9 - KNTT
- Giải sgk Giáo dục công dân 9 - KNTT
- Giải sgk Tin học 9 - KNTT
- Giải sgk Công nghệ 9 - KNTT
- Giải sgk Hoạt động trải nghiệm 9 - KNTT
- Giải sgk Âm nhạc 9 - KNTT
- Giải sgk Mĩ thuật 9 - KNTT
- Lớp 9 Chân trời sáng tạo
- Soạn văn 9 (hay nhất) - CTST
- Soạn văn 9 (ngắn nhất) - CTST
- Giải sgk Toán 9 - CTST
- Giải sgk Khoa học tự nhiên 9 - CTST
- Giải sgk Lịch Sử 9 - CTST
- Giải sgk Địa Lí 9 - CTST
- Giải sgk Giáo dục công dân 9 - CTST
- Giải sgk Tin học 9 - CTST
- Giải sgk Công nghệ 9 - CTST
- Giải sgk Hoạt động trải nghiệm 9 - CTST
- Giải sgk Âm nhạc 9 - CTST
- Giải sgk Mĩ thuật 9 - CTST
- Lớp 9 Cánh diều
- Soạn văn 9 Cánh diều (hay nhất)
- Soạn văn 9 Cánh diều (ngắn nhất)
- Giải sgk Toán 9 - Cánh diều
- Giải sgk Khoa học tự nhiên 9 - Cánh diều
- Giải sgk Lịch Sử 9 - Cánh diều
- Giải sgk Địa Lí 9 - Cánh diều
- Giải sgk Giáo dục công dân 9 - Cánh diều
- Giải sgk Tin học 9 - Cánh diều
- Giải sgk Công nghệ 9 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 9 - Cánh diều
- Giải sgk Âm nhạc 9 - Cánh diều
- Giải sgk Mĩ thuật 9 - Cánh diều

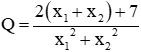
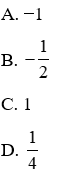
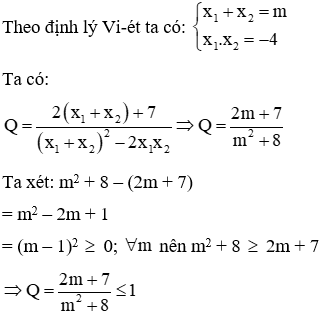
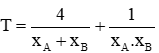
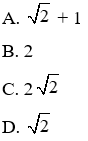
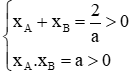
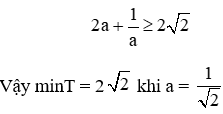
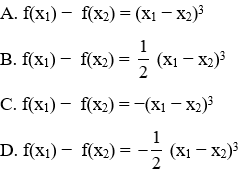
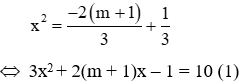
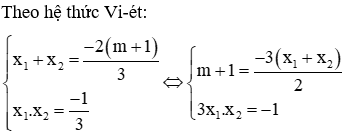
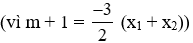
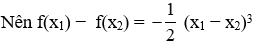
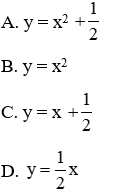
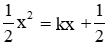
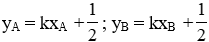
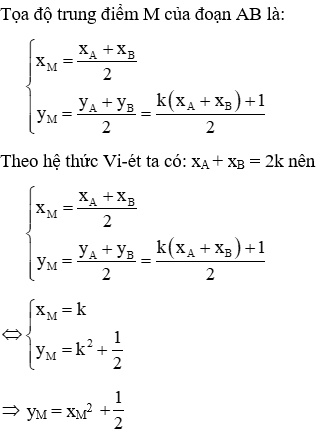
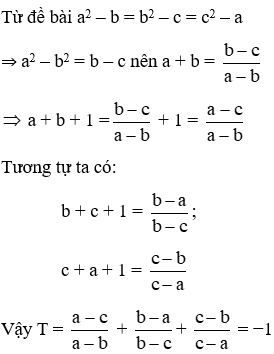
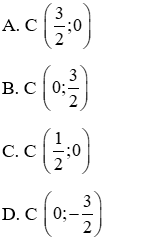
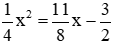
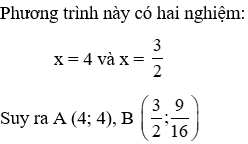
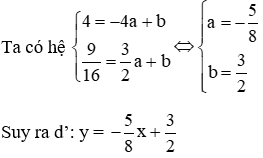
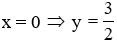
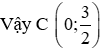

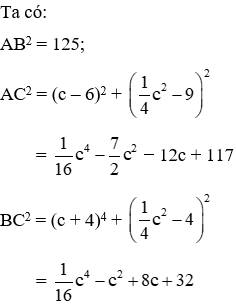
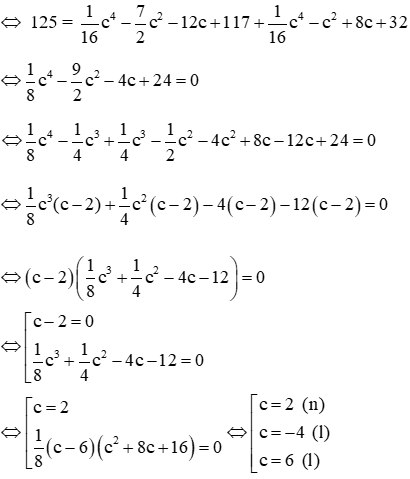



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

