Tuyển chọn 100 bài tập Tập hợp điểm số phức đầy đủ các dạng (ôn thi Tốt nghiệp)

Tuyển chọn 100 bài tập Tập hợp điểm số phức đầy đủ các dạng

Tài liệu Tuyển chọn 100 bài tập Tập hợp điểm số phức đầy đủ các dạng có lời giải chi tiết giúp học sinh củng cố kiến thức, ôn luyện để chuẩn bị tốt cho kì thi THPT Quốc gia môn Toán năm 2021.

Câu 1. Điểm M biểu diễn số phức z = 3 + 2i trong mặt phẳng tọa độ phức là:

A. M(3;2).           B. M(2;3).                              

C. M(3;-2).          D. M(-3;-2). 

Hướng dẫn giải

Số phức z có phần thực là 3, phần ảo là 2 nên điểm biểu diễn trên mặt phẳng tọa độ là điểm M(3;2) Đáp án A

Câu 2. Cho số phức z = -2i - 1. Điểm biểu diễn số phức liên hợp của z trong mặt phẳng phức là: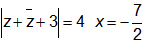

A. M(-1;-2).            B.M(-1;2).                            

C. M(-2;1).             D.M(2;-1). 

Hướng dẫn giải

Số phức liên hợp của z là |z - 1 + i| = |z + 1 - 2i| nên z = x + yi có phần thực là -1, phần ảo là 2. Vậy điểm biểu diễn số phức liên hợp là Đáp án B

Câu 3. Cho số phức 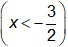. Điểm biểu diễn số phức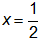trong mặt phẳng phức là:

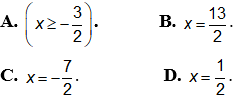
Hướng dẫn giải

Ta có : M(x,y) 

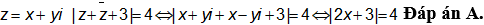
Câu 4. Gọi A là điểm biểu diễn của số phức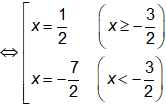và B là điểm biểu diễn của số phức M(x,y) . Trong các khẳng định sau, khẳng định nào đúng?

A. Hai điểm A và B đối xứng nhau qua trục tung.

B. Hai điểm A và B đối xứng nhau qua gốc tọa độ O.

C. Hai điểm A và B đối xứng nhau qua đường thẳng.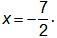

D. Hai điểm A và B đối xứng nhau qua trục hoành.

Hướng dẫn giải

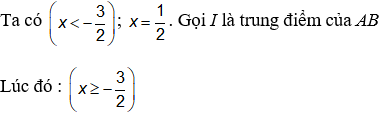
Với |z + i| = |z - i| và I là trung điểm của AB 

y =x A và B đối xứng nhau qua (d) y = -x Đáp án C

Câu 5. Gọi A là điểm biểu diễn số phức M(x,y), B là điểm biểu diễn số phức z = x + yi. Trong các khẳng định sau khẳng định nào sai ?

A. A và B đối xứng nhau qua trục hoành.

B. A và B trùng gốc tọa độ khi |z + i| = |z - i| ⇔ |x + (y + 1)i| = |x + (y - 1)i|.

C. A và B đối xứng qua gốc tọa độ.

D. Đường thẳng AB đi qua gốc tọa độ.

Hướng dẫn giải

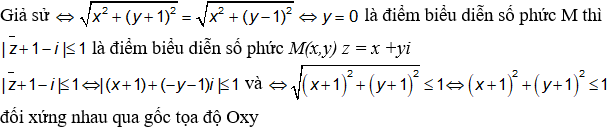
Đáp án A.

Câu 6. Các điểm biểu diễn các số phức z trong mặt phẳng tọa độ, nằm trên đường thẳng có phương trình là:

A.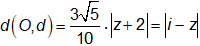

B. O. 

C. d.                                      

D. d. 

Hướng dẫn giải

Các điểm biểu diễn số phức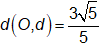có dạng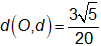nên nằm trên đường thẳng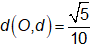

⇒ Đáp án D

Câu 7. Trên mặt phẳng tọa độ , tập hợp điểm biểu diễn các số phức Oxy thỏa mãn điều kiện phần thực của z bằng -2 là:

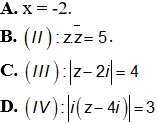
Hướng dẫn giải

Điểm biểu diễn các số phức (I) có phần thực bằng -2 có dạng M(-2;b) nên nằm trên đường thẳng x = -2 M(x,y) Đáp án A.

ĐÁP ÁN 

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
A	B	A	C	A	D	A	C	A	A	B	D	A	C	C	A	A	D	A	B
21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40
B	A	A	B	D	C	A	D	D	A	C	C	B	C	D	A	D	C	A	A
41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60
B	D	D	C	A	A	C	A	A	D

...................................................

...................................................

Để xem tài liệu đầy đủ, có đáp án chi tiết, bạn có thể tải xuống tài liệu ở đường dẫn bên dưới.

Xem thêm bộ tài liệu Toán lớp 12 ôn thi THPT Quốc gia chọn lọc, hay khác:

• Tuyển chọn 100 bài tập Tính đơn điệu của hàm số nắm chắc 8 điểm
• Tuyển chọn 104 bài tập Lũy thừa, mũ, logarit từ đề thi Đại học
• Tuyển chọn 125 bài tập Khảo sát hàm số nắm chắc 8 điểm
• 30 bài tập về Góc trong không gian có đáp án
• 30 Bài toán cực trị của số phức thường gặp

---