Trọn bộ Công thức Toán 11 Học kì 1, Học kì 2 (quan trọng, cả năm)

Nhằm mục đích giúp học sinh dễ dàng nhớ và nắm vững các công thức Toán 11 sách mới Kết nối tri thức, Chân trời sáng tạo, Cánh diều, tài liệu trọn bộ công thức Toán 11 Học kì 1, Học kì 2 Đại số và Hình học đầy đủ công thức quan trọng, lý thuyết và bài tập tự luyện giúp học sinh lớp 11 vận dụng và làm bài tập thật tốt môn Toán 11.

Trọn bộ Công thức Toán 11 Học kì 1, Học kì 2 (quan trọng, cả năm)

Công thức Toán 11 Kết nối tri thức

Công thức Toán 11 Chân trời sáng tạo

Công thức Toán 11 Cánh diều

Công thức Toán 11 Đại số

Công thức Toán 11 Hình học

Công thức Toán 11 Học kì 1

Công thức Toán 11 Dãy số - Cấp số cộng và cấp số nhân

• Công thức dãy số tăng, dãy số giảm

• Công thức dãy bị chặn

• Công thức để dãy số là cấp số cộng

• Công thức số hạng tổng quát và tính tổng n số hạng đầu của cấp số cộng

• Công thức để dãy số là cấp số nhân

• Công thức Số hạng tổng quát và tính tổng n số hạng đầu của cấp số nhân

Công thức Toán 11 Giới hạn. Hàm số liên tục

• Công thức tính tổng cấp số nhân lùi vô hạn

• Định lí về giới hạn hữu hạn và một số giới hạn cơ bản của dãy số

• Một số kết quả giới hạn cơ bản của hàm số

• Công thức hàm số liên tục tại một điểm, liên tục trên một khoảng hoặc một đoạn

Công thức Toán 11 Học kì 2

Công thức Toán 11 Hàm số mũ và hàm số lôgarit

• Công thức về phép tính lũy thừa với số mũ nguyên, số mũ hữu tỉ và số thực

• Công thức xác định lôgarit dựa vào định nghĩa

• Công thức tính lôgarit của một tích, một thương, một lũy thừa

• Công thức đổi cơ số của lôgarit

• Công thức Tập xác định của hàm số mũ, hàm số lôgarit

• Công thức nghiệm của phương trình mũ, phương trình lôgarit

• Công thức nghiệm của bất phương trình mũ, bất phương trình lôgari

Công thức Toán 11 Thống kê & Xác suất

• Công thức xác định số trung bình cộng của mẫu số liệu ghép nhóm

• Công thức xác định trung vị, tứ phân vị của mẫu số liệu ghép nhóm

• Công thức xác định mốt của mẫu số liệu ghép nhóm

• Công thức cộng xác suất

• Công thức nhân xác suất

Công thức Toán 11 Đạo hàm

• Công thức tính đạo hàm bằng định nghĩa

• Công thức tính đạo hàm của hàm sơ cấp cơ bản và tổng, hiệu, tích, thương

• Công thức tính đạo hàm của hàm hợp

• Công thức tính đạo hàm cấp hai

---

---

---

Lưu trữ: Công thức Toán 11 (sách cũ)

Chương 1: Hàm số lượng giác và phương trình lượng giác

• Công thức tính giá trị nhỏ nhất – giá trị lớn nhất của hàm số lượng giác

• Công thức giải phương trình lượng giác cơ bản

• Công thức biến đổi biểu thức asinx + bcosx

• Công thức gộp nghiệm phương trình lượng giác

Chương 2: Tổ hợp - Xác suất

• Công thức hoán vị

• Công thức chỉnh hợp

• Công thức tổ hợp

• Công thức khai triển nhị thức Niu-tơn

• Công thức tính tổng các hệ số trong khai triển

• Công thức tìm hệ số trong khai triển

• Công thức tìm số hạng trong khai triển

• Công thức tính xác suất

Chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng

• Công thức về phép tịnh tiến

• Công thức về phép đối xứng tâm

• Công thức về phép đối xứng trục

• Công thức về phép quay

• Công thức về phép vị tự

• Công thức về phép đồng dạng

Chương 3: Dãy số - Cấp số cộng và cấp số nhân

• Các công thức về cấp số cộng

• Công thức tính công sai của cấp số cộng

• Công thức tìm số hạng tổng quát của cấp số cộng

• Công thức tính tổng n số hạng của cấp số cộng

• Các công thức về cấp số nhân

• Công thức tính công bội của cấp số nhân

• Công thức số hạng tổng quát của cấp số nhân

• Công thức tổng n số hạng tổng quát của cấp số nhân

Chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song

• Công thức về giao tuyến của ba mặt phẳng và hệ quả

• Công thức chứng minh hai đường thẳng song song trong không gian

• Công thức chứng minh đường thẳng song song với mặt phẳng

• Công thức chứng minh hai mặt phẳng song song

• Định lý Ta-lét trong không gian

---

---

---

Công thức tính giá trị nhỏ nhất – giá trị lớn nhất của hàm số lượng giác

1. Lí thuyết

a) Sử dụng tính bị chặn của hàm số lượng giác

-1 ≤ sin[u(x)] ≤ 1; 0 ≤ sin²[u(x)] ≤ 1;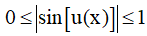  

-1 ≤ cos[u(x)] ≤ 1; 0 ≤ cos²[u(x)] ≤ 1;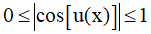  

b) Dạng y = asinx + bcosx + c  

Bước 1: Đưa hàm số về dạng chỉ chứa sin[u(x)] hoặc cos[u(x)]:

y = asinx + bcosx + c =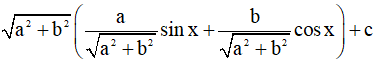   

⇔ y = 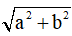.sin(x + α ) + c với α thỏa mãn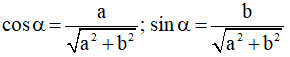

Bước 2: Đánh giá -1 ≤ sin[x + α] ≤ 1 ∀x ∈ R 

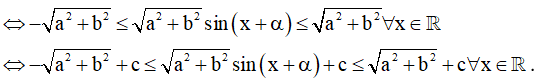
2. Công thức

a) Dạng y = asin[u(x)] + b hoặc y = acos[u(x)] + b

Ta có: –|a| + b ≤ y ≤ |a| + b 

Hàm số có giá trị nhỏ nhất là –|a| + b và giá trị lớn nhất là |a| + b.

b) Dạng y = asin²[u(x)] + b ; y = a|sin[u(x)]| + b; 

Dạng y = acos²[u(x)] + b; y = a|cos[u(x)]| + b (với a khác 0)

+ Trường hợp 1: a > 0. Ta có: b ≤ y ≤ a + b  .

Hàm số có giá trị nhỏ nhất là b và giá trị lớn nhất là a + b.

+ Trường hợp 2: a < 0. Ta có: a + b ≤ y ≤ b .

Hàm số có giá trị nhỏ nhất là a + b và giá trị lớn nhất là b.

c) Dạng y = asinx + bcosx + c

Ta có: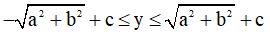   

Hàm số có giá trị nhỏ nhất là 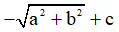 và giá trị lớn nhất là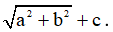 

Công thức giải phương trình lượng giác cơ bản

1. Lí thuyết

* Công thức nghiệm cơ bản

a) Phương trình sin x = m 

Trường hợp 1: |m| > 1. Phương trình vô nghiệm.

Trường hợp 2: |m| ≤ 1. Phương trình có nghiệm.

- Nếu m biểu diễn được dưới dạng sin của những góc đặc biệt thì:

sinx = m ⇔ sinx = sinα ⇔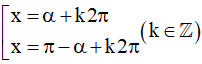  

- Nếu m không biểu diễn được dưới dạng sin của những góc đặc biệt thì:

sinx = m ⇔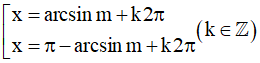

- Các trường hợp đặc biệt:

sinx = 0 ⇔ x = kπ (k ∈ Z)

sinx = 1 ⇔ x = 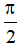 + k2π (k ∈ Z)

sinx = -1 ⇔ x = -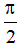 + k2π (k ∈ Z)

b) Phương trình cos x = m

Trường hợp 1: |m| > 1. Phương trình vô nghiệm.

Trường hợp 2: |m| ≤ 1 . Phương trình có nghiệm.

- Nếu m biểu diễn được dưới dạng cos của những góc đặc biệt thì:

 

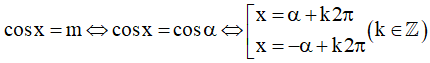
- Nếu m không biểu diễn được dưới dạng cos của những góc đặc biệt thì:

 

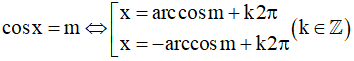
- Các trường hợp đặc biệt:

cosx = 0 ⇔ x = 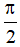 + kπ (k ∈ Z)

cosx = 1 ⇔ x = k2π (k ∈ Z)

cosx = -1 ⇔ x = π + k2π (k ∈ Z)

c) Phương trình: tan x = m. Điều kiện: x ≠ 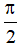+ kπ (k ∈ Z)

- Nếu m biểu diễn được dưới dạng tan của những góc đặc biệt thì:

tan x = m ⇔ tan x = tan α ⇔ x = α + kπ (k ∈ Z)   

- Nếu m không biểu diễn được dưới dạng tan của những góc đặc biệt thì:

tan x = m ⇔ x = αrctan m + kπ (k ∈ Z)

d) Phương trình: cot x = m. Điều kiện: x ≠ kπ (k ∈ Z) 

- Nếu m biểu diễn được dưới dạng cot của những góc đặc biệt thì:

cot x = m ⇔ cot x = cot α ⇔ x = α + kπ (k ∈ Z) 

- Nếu m không biểu diễn được dưới dạng cot của những góc đặc biệt thì:

cot x = m ⇔ x = αrccot m + kπ (k ∈ Z)

* Mở rộng công thức nghiệm, với u(x) và v(x) là hai biểu thức của x.

 

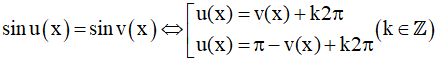
cos u(x) = cos v(x) ⇔ u(x) = 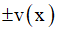 + k2π (k ∈ Z)

tan u(x) = tan v(x) ⇔ u(x) = v(x) + kπ (k ∈ Z)

cot u(x) = cot v(x) ⇔ u(x) = v(x) + kπ (k ∈ Z) 

2. Công thức

Khi đã cho số m, ta có thể tìm các giá trị arcsin m, arccos m, arctan m, arccot m bằng máy tính bỏ túi với các phím sin^-1; cos^-1; tan^-1.

Bước 1. Chỉnh chế độ rad hoặc độ

- Muốn tìm số đo radian: 

ta ấn qw4 (đối với Casio fx - 570VN) 

ta ấn qw22 (đối với Casio fx - 580VN X)

-  Muốn tìm số đo độ: 

ta ấn qw3 (đối với Casio fx - 570VN) 

ta ấn qw21 (đối với Casio fx - 580VN X)

Bước 2. Tìm số đo góc

Tìm góc α khi biết sin của góc đó bằng m, ta ấn lần lượt qj m =.

Tương tự đối với cos và tan.

Chú ý: Muốn tìm góc α khi biết cot của góc đó bằng m, ta ấn lần lượt ql1a m $)=.

Sau đó áp dụng công thức lượng giác để giải phương trình.

..........................

..........................

..........................

Trên đây là tóm lược một số nội dung có trong tổng hợp công thức Toán lớp 11 Học kì 1 và Học kì 2, mời quí bạn đọc vào từng bài để xem đầy đủ, chi tiết!

---