Tổng hợp công thức giải nhanh Toán lớp 11 Học kì 2 chi tiết
Việc nhớ chính xác một công thức Toán lớp 11 trong hàng trăm công thức không phải là việc dễ dàng, với mục đích giúp học sinh dễ dàng hơn trong việc nhớ Công thức, VietJack biên soạn bản tóm tắt Tổng hợp công thức giải nhanh Toán lớp 11 Đại số và Hình học Học kì 2 chi tiết, đầy đủ cả năm. Hi vọng loạt bài này sẽ như là cuốn sổ tay công thức giúp bạn học tốt môn Toán lớp 11 hơn.
Tổng hợp công thức Toán 11 Học kì 2 (sách mới)
Bộ công thức Toán 11 dưới đây được sắp xếp theo tiến trình học của sách Toán 11 Kết nối tri thức. Học sinh học theo 2 bộ sách Toán 11 còn lại (Chân trời sáng tạo & Cánh diều) có thể dễ dàng tra cứu theo nội dung công thức hoặc có trong Công thức Toán 11 (sách mới, đầy đủ).
Công thức Toán 11 Hàm số mũ và hàm số lôgarit
Công thức về phép tính lũy thừa với số mũ nguyên, số mũ hữu tỉ và số thực
Công thức tính lôgarit của một tích, một thương, một lũy thừa
Công thức nghiệm của bất phương trình mũ, bất phương trình lôgari
Công thức Toán 11 Thống kê & Xác suất
Công thức xác định số trung bình cộng của mẫu số liệu ghép nhóm
Công thức xác định trung vị, tứ phân vị của mẫu số liệu ghép nhóm
Công thức Toán 11 Đạo hàm
Công thức Toán 11 Quan hệ song song và quan hệ vuông góc
Lưu trữ: Công thức Toán 11 Học kì 2 (sách cũ)
Công thức giải nhanh Toán lớp 11 Chương 2 Hình học chi tiết nhất
Công thức giải nhanh Toán lớp 11 Chương 3 Hình học chi tiết nhất
Công thức giải nhanh Toán lớp 11 Chương 4 Đại số
I. Giới hạn của dãy số
1. Một số giới hạn cơ bản
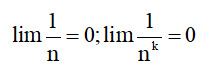
limnk = + 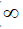
limC = C với C là hằng số.
2. Tính chất (Áp dụng khi tồn tại limun; limvn)
3. Cách tìm giới hạn dãy số:
- Nếu biểu thức có dạng phân thức mà mẫu và tử đều chứa luỹ thừa của n , ta chia tử và mẫu cho nk với k là số mũ cao nhất.
- Nếu biểu thức đã cho có chứa n dưới dấu căn thì có thể nhân tử và mẫu với cùng một biểu thức liên hợp.
II. Giới hạn của hàm số
1. Một số giới hạn cần nhớ
2. Tính chất (dùng khi tồn tại 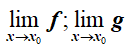
3. Tính chất
(bằng +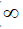
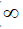
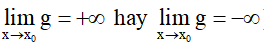
(bằng + 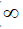
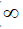
4. Giới hạn trái - giới hạn phải
+) Giới hạn bên trái,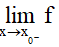
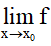
+) Giới hạn bên phải, 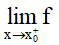
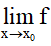
+) 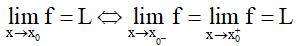
5. Phương pháp tìm giới hạn hàm số
+) Dạng 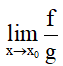
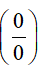
- Dùng lược đồ Hoocne.
- Nếu f;g chứa biến trong căn, ta nhân tử mẫu cho biểu thức liên hợp.
+) Dạng 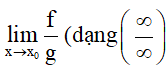
- Chia tử, mẫu cho xn với n là số mũ cao nhất.
- Nếu f;g chứa biến trong căn, ta đưa xk ra ngoài dấu căn (với k là số mũ cao nhất trong căn), rồi chia tử và mẫu cho luỹ thừa của x
+) Dạng 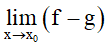
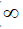
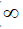
Dạng 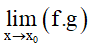
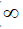
Nhân và chia với biểu thức liên hợp hoặc qui đồng mẫu.
III. Hàm số liên tục
1. Hàm số liên tục bên trái
f liên tục trái tại x0 ⇔
2. Hàm số liên tục bên phải
f liên tục phải tại x0 ⇔
3. Hàm số liên tục
f liên tục tại x0 ⇔
4. Chứng minh phương trình f = 0 có ít nhất một nghiệm trong khoảng (a; b)
phương trình 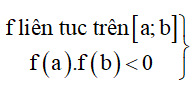
Công thức giải nhanh Toán lớp 11 Chương 2 Hình học
1. Vị trí tương đối giữa đường thẳng và mặt phẳng
2. Vị trí tương đối giữa hai mặt phẳng
3. Vị trí tương đối giữa hai đường thẳng
4. Cách xác định giao tuyến giữa hai mặt phẳng
Cách 1: Tìm hai điểm chung của hai mặt phẳng.
Chú ý: Để tìm điểm chung của hai mặt phẳng ta thường tìm hai đường thẳng đồng phẳng lần lượt nằm trong hai mặt phẳng. Giao điểm, nếu có, của hai đường thẳng này chính là điểm chung cần tìm
Cách 2: Tìm một điểm chung của hai mặt phẳng và phương giao tuyến (tức tìm trong hai mặt phẳng hai đường thẳng song song với nhau).
5. Cách xác định giao điểm giữa đường thẳng và mặt phẳng
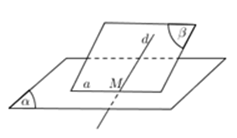
Để tìm giao điểm của d và (α) , ta tìm trong (α) một đường thẳng a cắt d tại M . Khi đó: M = d ∩ (α) .
Chú ý: Nếu a chưa có sẵn thì ta chọn (β) qua d và lấy a = (α) ∩ (β).
6. Thiết diện
Thiết diện của mặt phẳng (α) với hình chóp là đa giác giới hạn bởi các giao tuyến của (α) với các mặt của hình chóp. Như vậy, để tìm thiết diện ta lần lượt đi tìm giao tuyến của (α) với các mặt của hình chóp.
7. Chứng minh đường thẳng song song đường thẳng
Cách 1: Chứng minh hai đường thẳng đồng phẳng rồi áp dụng phương pháp chứng minh song song trong hình học phẳng (đường trung bình; định lí Tales…)
Cách 2: Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.
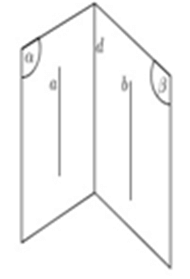
Cách 3: Hai mặt phẳng cắt nhau theo giao tuyến và lần lượt chứa hai đường thẳng song song thì giao tuyến của nó sẽ có 3 trường hợp:
Như vậy, trong trường hợp này ta chỉ cần chỉ ra d không trùng với a hoặc b thì sẽ suy ra được 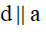
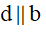
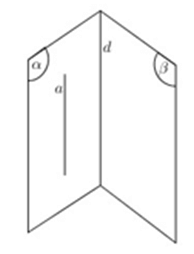
Cách 4: Hai mặt phẳng cắt nhau theo giao tuyến , đường thẳng nằm trong và song song với mặt phẳng còn lại thì sẽ song song với giao tuyến.
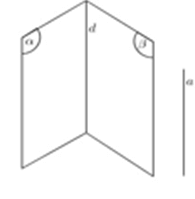
Cách 5: Hai mặt phẳng cắt nhau theo giao tuyến d , đường thẳng a song song với cả hai mặt phẳng thì sẽ song song với giao tuyến.
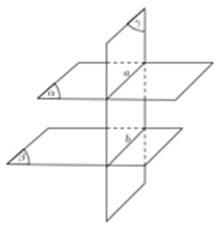
Cách 6: Hai mặt phẳng song song bị cắt bởi mặt phẳng thứ 3 thì hai giao tuyến đó song song.
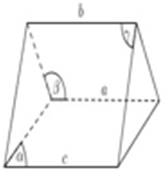
Cách 7: Ba mặt phẳng cắt nhau theo 3 giao tuyến phân biệt, thì 3 giao tuyến ấy song song hoặc đồng quy.
Như vậy, ta chỉ cần chứng minh a;b;c không đồng quy thì sẽ suy ra được 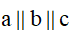
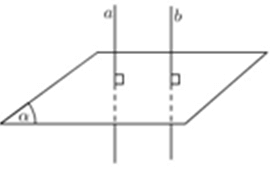
Cách 8: Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
8. Chứng minh đường thẳng song song với mặt phẳng
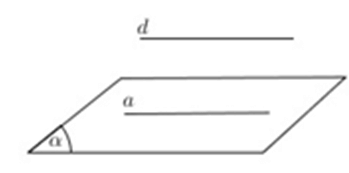
Cách 1: Chứng minh đường thẳng d không nằm trong (α) và song song với đường thẳng a nằm trong (α) .
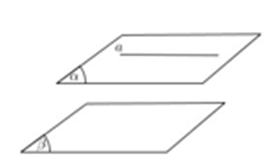
Cách 2: Hai mặt phẳng song song với nhau, mọi đường thẳng nằm trong mặt này sẽ song song với mặt kia.
9. Chứng minh hai mặt phẳng song song
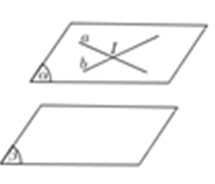
Cách 1: Chứng minh trong mặt phẳng thứ nhất chứa hai đường thẳng cắt nhau và song song mặt phẳng thứ hai, khi đó hai mặt phẳng song song với nhau.
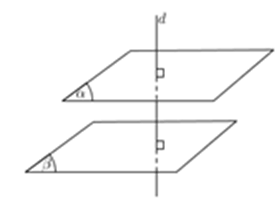
Cách 2: Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
Xem thêm tổng hợp công thức môn Toán lớp 11 đầy đủ và chi tiết khác:
Công thức giải nhanh Toán lớp 11 Chương 1 Đại số chi tiết nhất
Công thức giải nhanh Toán lớp 11 Chương 2 Đại số chi tiết nhất
Công thức giải nhanh Toán lớp 11 Chương 3 Đại số chi tiết nhất
Công thức giải nhanh Toán lớp 11 Chương 1 Hình học chi tiết nhất
Tủ sách VIETJACK shopee lớp 6-8 (2025):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Loạt bài 500 Công thức, Định Lí, Định nghĩa Toán, Vật Lí, Hóa học, Sinh học được biên soạn bám sát nội dung chương trình học các cấp.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Đề thi lớp 1 (các môn học)
- Đề thi lớp 2 (các môn học)
- Đề thi lớp 3 (các môn học)
- Đề thi lớp 4 (các môn học)
- Đề thi lớp 5 (các môn học)
- Đề thi lớp 6 (các môn học)
- Đề thi lớp 7 (các môn học)
- Đề thi lớp 8 (các môn học)
- Đề thi lớp 9 (các môn học)
- Đề thi lớp 10 (các môn học)
- Đề thi lớp 11 (các môn học)
- Đề thi lớp 12 (các môn học)
- Giáo án lớp 1 (các môn học)
- Giáo án lớp 2 (các môn học)
- Giáo án lớp 3 (các môn học)
- Giáo án lớp 4 (các môn học)
- Giáo án lớp 5 (các môn học)
- Giáo án lớp 6 (các môn học)
- Giáo án lớp 7 (các môn học)
- Giáo án lớp 8 (các môn học)
- Giáo án lớp 9 (các môn học)
- Giáo án lớp 10 (các môn học)
- Giáo án lớp 11 (các môn học)
- Giáo án lớp 12 (các môn học)

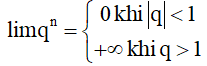
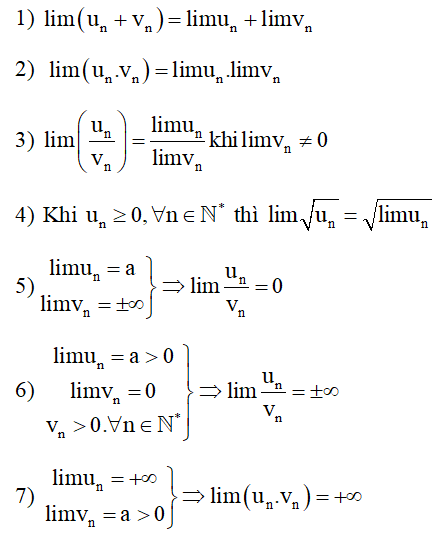
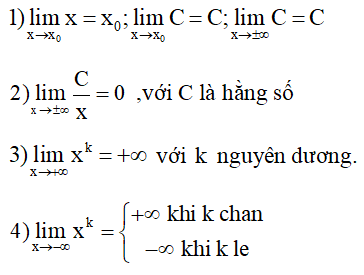
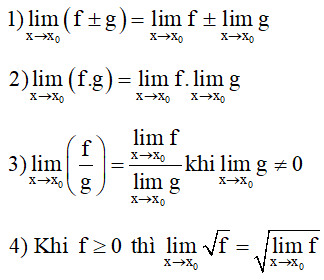
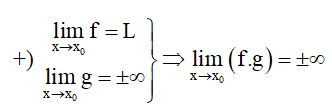
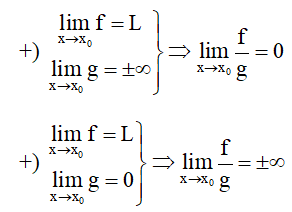
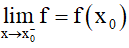
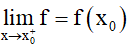
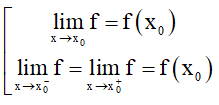
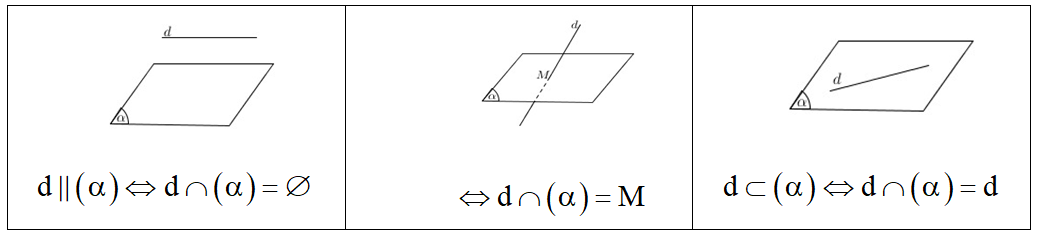
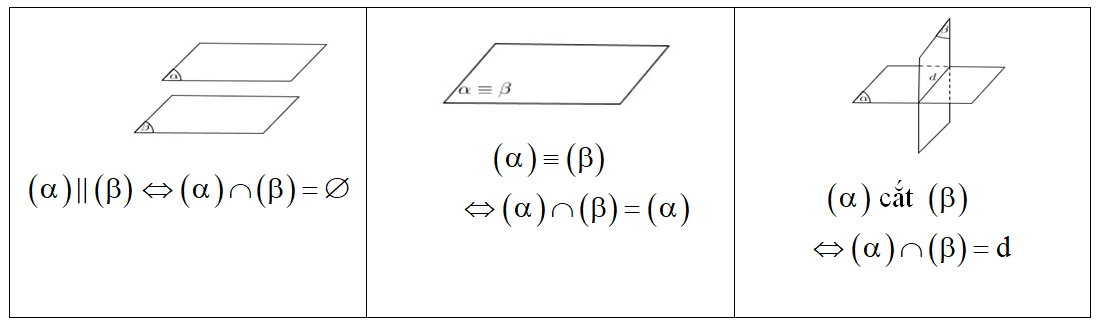
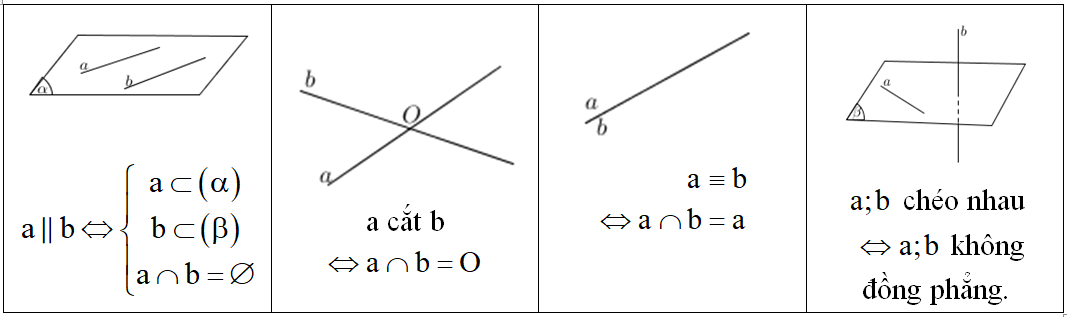
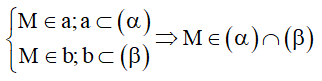
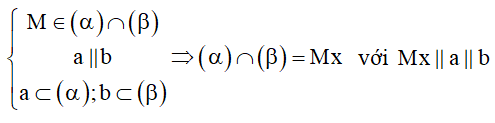
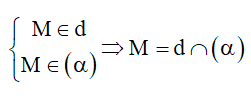

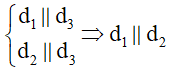
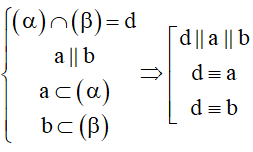
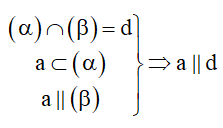
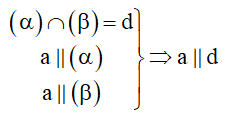
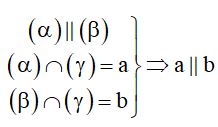
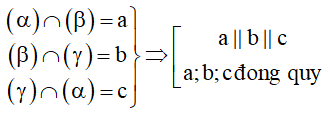
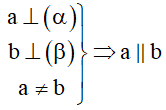
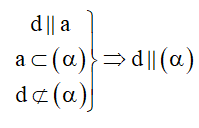
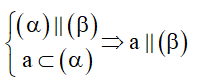
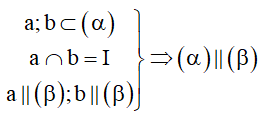
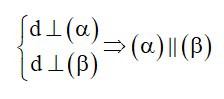






 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

