Công thức Toán 11 Hình học (cả năm - sách mới)
Việc nhớ chính xác một công thức Toán lớp 11 trong hàng trăm công thức không phải là việc dễ dàng, với mục đích giúp học sinh dễ dàng hơn trong việc nhớ Công thức, VietJack biên soạn bản tóm tắt Công thức giải nhanh Hình học lớp 11 Học kì 1, Học kì 2 đầy đủ, chi tiết nhất. Hi vọng loạt bài này sẽ như là cuốn sổ tay công thức giúp bạn học tốt môn Toán lớp 11 hơn.
Công thức Toán 11 Hình học (cả năm - sách mới)
Công thức Toán 11 Quan hệ song song và quan hệ vuông góc
Lưu trữ: Công thức Toán 11 Hình học (sách cũ)
Công thức giải nhanh Toán lớp 11 Chương 1 Hình học chi tiết nhất
Công thức giải nhanh Toán lớp 11 Chương 3 Hình học chi tiết nhất
Công thức giải nhanh Toán lớp 11 Chương 1 Hình học
1. Đại cương về phép biến hình
PBH F : 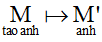
- Hình H' = F(H) ⇔ H' = 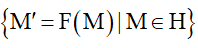
- O = F(O) ⇔ O là điểm bất động.
- PBH mà mọi điểm trong mặt phẳng đều biến thành chính nó được gọi là phép đồng nhất. Kí hiệu .
- 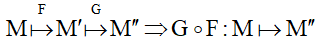
2. Phép dời hình
PBH F là PDH và A' = F(A); B' = F(B) thì A'B' = AB (bảo toàn khoảng cách giữa hai điểm bất kì)
PDH biến
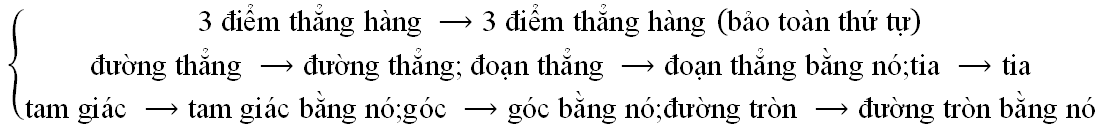
3. Phép tịnh tiến theo 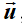
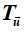
4. Phép đối xứng trục (ĐXTR) d , kí hiệu Đd
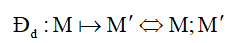
5. Phép đối xứng tâm (ĐXT) I , kí hiệu ĐI
6. Phép vị tự (PVT) tâm I tỉ số k , kí hiệu V(I;k)
7. Phép đồng dạng (PĐD)
PĐD tỉ số k (k > 0) là PBH sao cho với hai điểm A;B bất kì và ảnh A';B' của nó ta có A'B' = kAB
PĐD biến
8. Biểu thức tọa độ
Giả sử M(x;y) , M(x';y') .
+) PTT theo 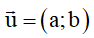
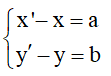
+) Phép đối xứng tâm I(a;b) là 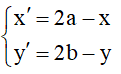
+) Phép đối xứng trục d khi
+) Phép quay tâm I(a;b) , góc α là
Đặc biệt: Tâm quay là O(0;0) thì
Phép vị tự tâm I(a;b) , tỉ số k là 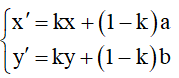
9. Ảnh của đường thẳng d qua PTT; phép ĐXT; PQ; PVT
Giả sử F: 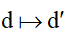
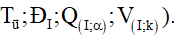
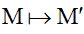
Viết biểu thức tọa độ tương ứng với PBH đề cho ⇒ 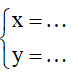
Ta có M ∈ d (thay x;y vào đường thẳng d ) ta được đường thẳng d' .
10. Ảnh của đường tròn
Giả sử F: 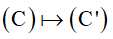
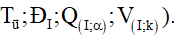
Xác định tâm I của đường tròn (C) . Tìm ảnh I' của I qua PBH F .
Ta có: 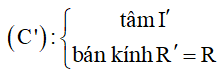

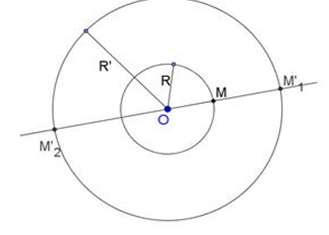
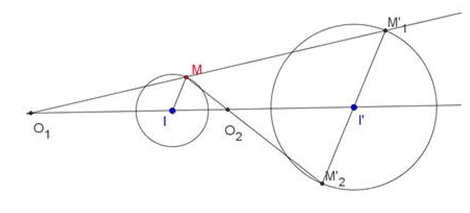
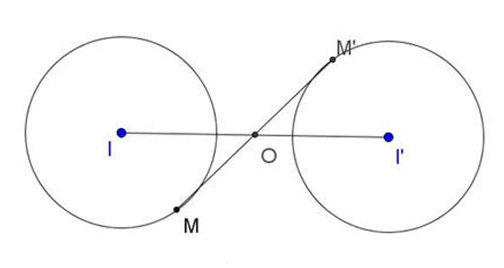
11. Tâm vị tự của hai đường tròn
TH1: Nếu I ≡ I' thì PVT tâm O ≡ I, tỉ số 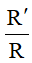
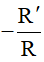
TH2: Nếu I ≠ I' và R ≠ R' thì PVT tâm O1 (tâm vị tự ngoài), tỉ số 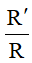
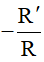
TH3: Nếu I ≠ I' và R = R' thì PVT tâm O, tỉ số k = 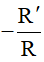
Công thức giải nhanh Toán lớp 11 Chương 2 Hình học
1. Vị trí tương đối giữa đường thẳng và mặt phẳng
2. Vị trí tương đối giữa hai mặt phẳng
3. Vị trí tương đối giữa hai đường thẳng
4. Cách xác định giao tuyến giữa hai mặt phẳng
Cách 1: Tìm hai điểm chung của hai mặt phẳng.
Chú ý: Để tìm điểm chung của hai mặt phẳng ta thường tìm hai đường thẳng đồng phẳng lần lượt nằm trong hai mặt phẳng. Giao điểm, nếu có, của hai đường thẳng này chính là điểm chung cần tìm
Cách 2: Tìm một điểm chung của hai mặt phẳng và phương giao tuyến (tức tìm trong hai mặt phẳng hai đường thẳng song song với nhau).
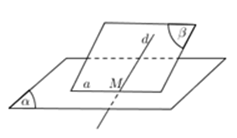
5. Cách xác định giao điểm giữa đường thẳng và mặt phẳng
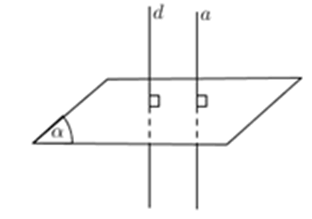
Để tìm giao điểm của d và (α) , ta tìm trong (α) một đường thẳng a cắt d tại M . Khi đó: M = d ∩ (α) .
Chú ý: Nếu a chưa có sẵn thì ta chọn (β) qua d và lấy a = (α) ∩ (β).
6. Thiết diện
Thiết diện của mặt phẳng (α) với hình chóp là đa giác giới hạn bởi các giao tuyến của (α) với các mặt của hình chóp. Như vậy, để tìm thiết diện ta lần lượt đi tìm giao tuyến của (α) với các mặt của hình chóp.
7. Chứng minh đường thẳng song song đường thẳng
Cách 1: Chứng minh hai đường thẳng đồng phẳng rồi áp dụng phương pháp chứng minh song song trong hình học phẳng (đường trung bình; định lí Tales…)
Cách 2: Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.
Cách 3: Hai mặt phẳng cắt nhau theo giao tuyến và lần lượt chứa hai đường thẳng song song thì giao tuyến của nó sẽ có 3 trường hợp:
Như vậy, trong trường hợp này ta chỉ cần chỉ ra d không trùng với a hoặc b thì sẽ suy ra được 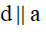
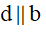
Cách 4: Hai mặt phẳng cắt nhau theo giao tuyến , đường thẳng nằm trong và song song với mặt phẳng còn lại thì sẽ song song với giao tuyến.
Cách 5: Hai mặt phẳng cắt nhau theo giao tuyến d , đường thẳng a song song với cả hai mặt phẳng thì sẽ song song với giao tuyến.
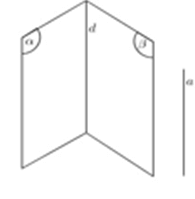
Cách 6: Hai mặt phẳng song song bị cắt bởi mặt phẳng thứ 3 thì hai giao tuyến đó song song.
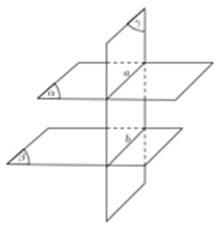
Cách 7: Ba mặt phẳng cắt nhau theo 3 giao tuyến phân biệt, thì 3 giao tuyến ấy song song hoặc đồng quy.
Như vậy, ta chỉ cần chứng minh a;b;c không đồng quy thì sẽ suy ra được 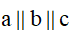
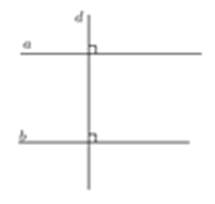
Cách 8: Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
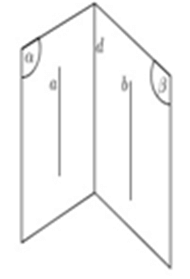
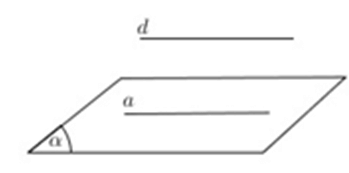
8. Chứng minh đường thẳng song song với mặt phẳng
Cách 1: Chứng minh đường thẳng d không nằm trong (α) và song song với đường thẳng a nằm trong (α) .
Cách 2: Hai mặt phẳng song song với nhau, mọi đường thẳng nằm trong mặt này sẽ song song với mặt kia.
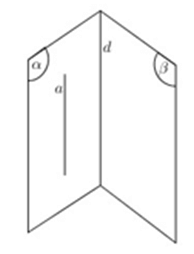
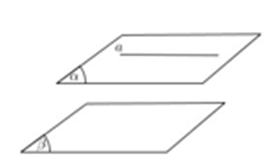
9. Chứng minh hai mặt phẳng song song
Cách 1: Chứng minh trong mặt phẳng thứ nhất chứa hai đường thẳng cắt nhau và song song mặt phẳng thứ hai, khi đó hai mặt phẳng song song với nhau.
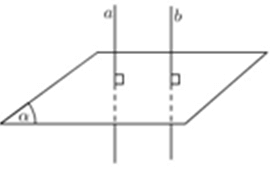
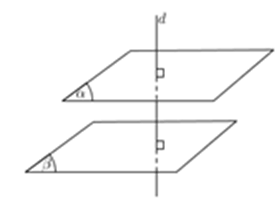
Cách 2: Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
Công thức giải nhanh Toán lớp 11 Chương 3 Hình học
1. Chứng minh hai đường thẳng vuông góc
Cách 1: Hai đường thẳng vuông góc nếu như góc giữa chúng bằng 90o .
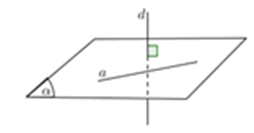
Cách 2: Một đường thẳng vuông góc với mặt phẳng thì sẽ vuông góc với mọi đường nằm trong mặt phẳng.
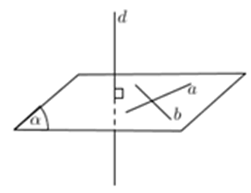
Cách 3: Đường thẳng d không vuông góc (α) và đường thẳng a nằm trong (α) . Khi đó, điều kiện cần và đủ để d vuông a là d vuông với hình chiếu a' của a trên (α)
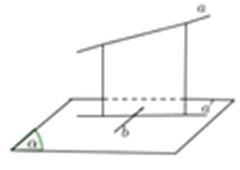
Cách 4: Hai đường thẳng song song, một đường vuông góc với đường này thì vuông góc với đường kia.
2. Chứng minh đường thẳng vuông góc mặt phẳng
Cách 1: Một đường thẳng vuông góc với một mặt phẳng khi chỉ khi đường thẳng ấy vuông góc với hai đường thẳng cắt nhau chứa trong mặt phẳng.
Cách 2: Hai đường thẳng song song đường này vuông góc với mặt phẳng thì đường kia cũng vuông góc mặt phẳng.
Cách 3: Một đường thẳng vuông góc với một trong hai mặt phẳng song song thì vuông góc với mặt còn lại.
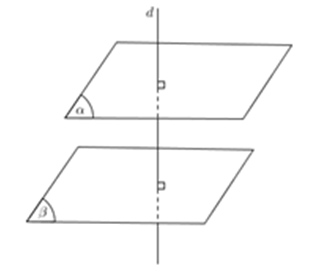
Cách 4: Hai mặt phẳng cắt nhau cùng vuông góc mặt phẳng thứ ba thì giao tuyến vuông góc với mặt phẳng thứ ba.
Cách 5: Hai mặt phẳng vuông góc, một đường nằm trong mặt này vuông với giao tuyến thì vuông với mặt kia.
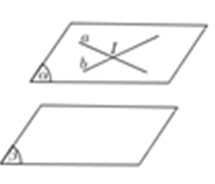
3. Chứng minh hai mặt phẳng vuông góc
Hai mặt phẳng vuông góc với nhau khi và chỉ khi mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
4. Góc
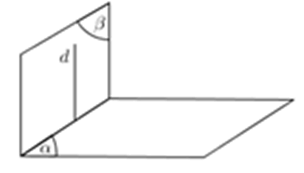
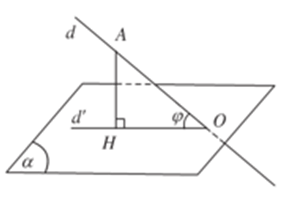
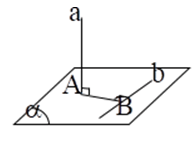
a) Góc giữa đường thẳng và mặt phẳng
- Tìm giao điểm O của d và (α) .
- Chọn điểm A ∈ d , dựng AH ⊥ (α) (H ∈ (α)) .
- Suy ra, hình chiếu vuông góc của AO trên (α) là MO .
Do đó: 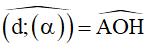
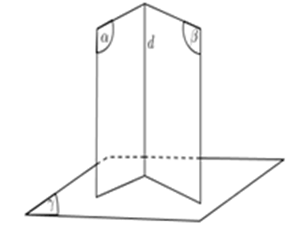
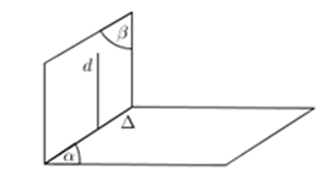
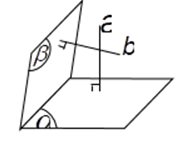
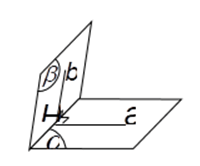
b) Góc giữa hai mặt phẳng
Cách 1: Tìm hai đường thẳng a;b sao cho 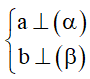
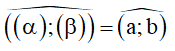
Cách 2:
- Xác định c = (α) ∩ (β) .
- Từ H ∈ c , lần lượt dựng 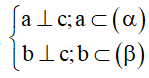
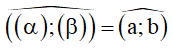
5. Khoảng cách
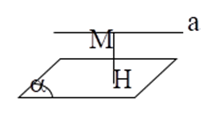
a) Khoảng cách từ một điểm đến một mặt phẳng
- Chọn trong (α) một đường thẳng d rồi dựng mặt phẳng (β) qua A vuông góc với d
- Xác định c = (α) ∩ (β) .
- Dựng AH ⊥ c tại H . Đường thẳng AH là đường thẳng qua A vuông góc (α) .
- Khi đó, độ dài đoạn thẳng AH là khoảng cách từ A đến (α) . Kí hiệu d(A;(α)) .
Chú ý:
1) Nếu đã có sẵn đường thẳng Δ (α) , khi đó chỉ cần dựng đường thẳng 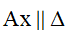
2) Nếu AB // (α) thì d(A;(α)) = d(B;(α)) . Nếu AB cắt (α) tại I thì 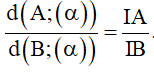
b) Khoảng cách từ đường thẳng a đến mặt phẳng (α) song song với a là
d(a;(α)) = d(M;(α)) với M ∈ a
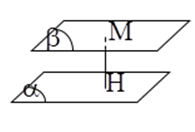
c) Khoảng cách giữa hai mặt phẳng song song (α) và (β) là
d((α);(β)) = d(M;(β)) với M ∈ (α) .
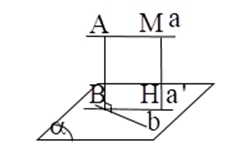
d) Đoạn vuông góc chung – khoảng cách giữa hai đường thẳng chéo nhau
Cách 1: (áp dụng cho trường hợp a ⊥ b )
Dựng (α) chứa b , vuông góc với a tại A .
Dựng AB ⊥ b tại B . Khi đó, a(a;b) = AB
Cách 2: Dựng mặt phẳng chứa b , song song với a . Khi đó, d(a;b) = AB = MH = d(a;(α))
Xem thêm tổng hợp công thức môn Toán lớp 11 đầy đủ và chi tiết khác:
Công thức giải nhanh Toán lớp 11 Chương 1 Đại số chi tiết nhất
Công thức giải nhanh Toán lớp 11 Chương 2 Đại số chi tiết nhất
Công thức giải nhanh Toán lớp 11 Chương 3 Đại số chi tiết nhất
Công thức giải nhanh Toán lớp 11 Chương 4 Đại số chi tiết nhất
Công thức giải nhanh Toán lớp 11 Chương 5 Đại số chi tiết nhất
Tủ sách VIETJACK shopee lớp 6-8 (2025):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Loạt bài 500 Công thức, Định Lí, Định nghĩa Toán, Vật Lí, Hóa học, Sinh học được biên soạn bám sát nội dung chương trình học các cấp.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Đề thi lớp 1 (các môn học)
- Đề thi lớp 2 (các môn học)
- Đề thi lớp 3 (các môn học)
- Đề thi lớp 4 (các môn học)
- Đề thi lớp 5 (các môn học)
- Đề thi lớp 6 (các môn học)
- Đề thi lớp 7 (các môn học)
- Đề thi lớp 8 (các môn học)
- Đề thi lớp 9 (các môn học)
- Đề thi lớp 10 (các môn học)
- Đề thi lớp 11 (các môn học)
- Đề thi lớp 12 (các môn học)
- Giáo án lớp 1 (các môn học)
- Giáo án lớp 2 (các môn học)
- Giáo án lớp 3 (các môn học)
- Giáo án lớp 4 (các môn học)
- Giáo án lớp 5 (các môn học)
- Giáo án lớp 6 (các môn học)
- Giáo án lớp 7 (các môn học)
- Giáo án lớp 8 (các môn học)
- Giáo án lớp 9 (các môn học)
- Giáo án lớp 10 (các môn học)
- Giáo án lớp 11 (các môn học)
- Giáo án lớp 12 (các môn học)

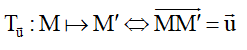
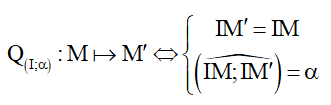
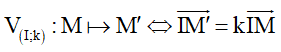
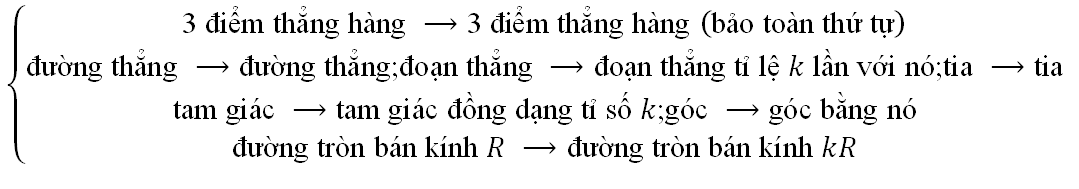
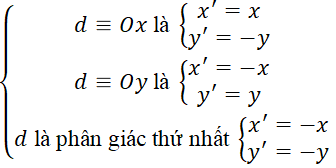
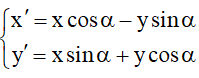
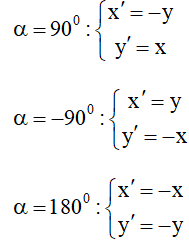
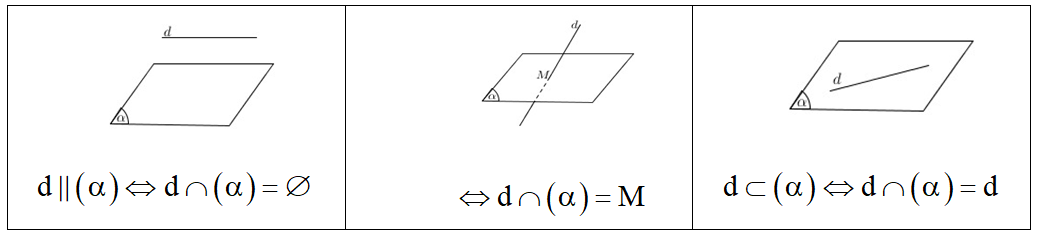
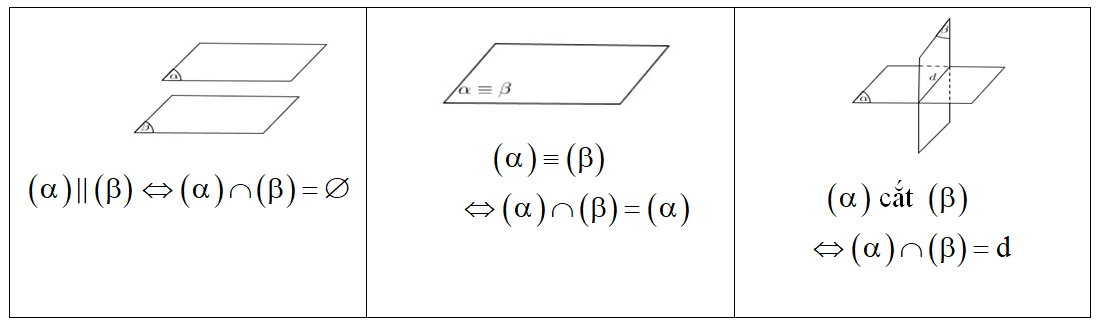
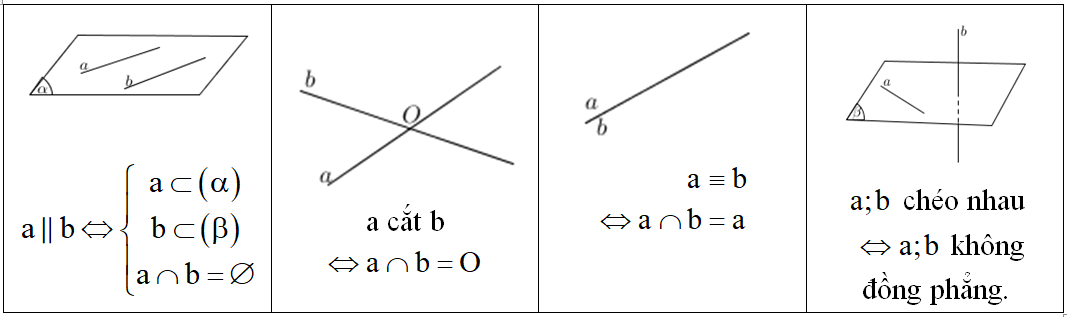
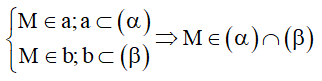
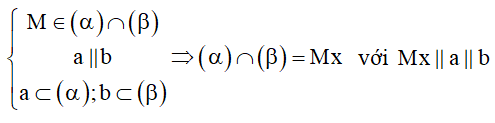
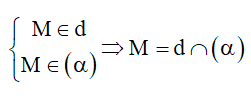

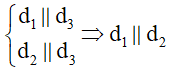
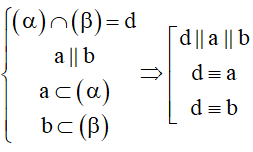
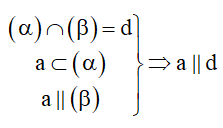
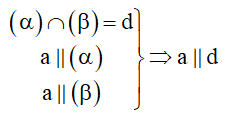
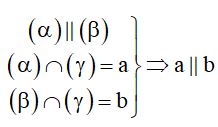
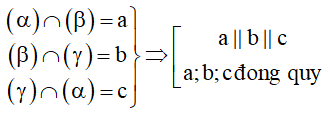
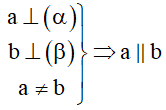
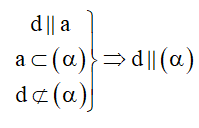
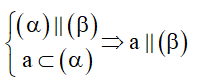
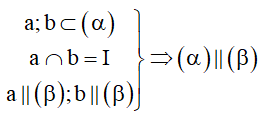
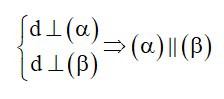
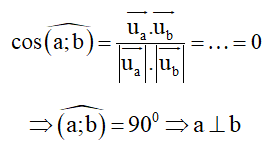
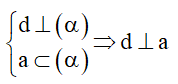

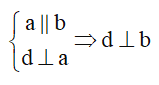
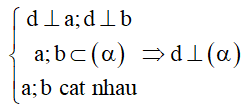
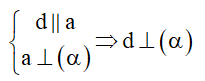
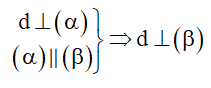
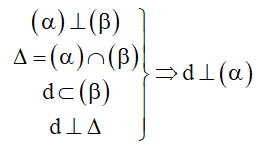
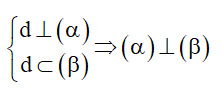






 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

