Trọn bộ Công thức Toán lớp 11 Chương 3: Dãy số - Cấp số cộng và cấp số nhân quan trọng

---

---

Trọn bộ Công thức Toán lớp 11 Chương 3: Dãy số - Cấp số cộng và cấp số nhân quan trọng

Nhằm mục đích giúp học sinh dễ dàng nhớ và nắm vững các công thức Toán 11, VietJack biên soạn tài liệu trọn bộ công thức Toán 11 Chương 3: Dãy số - Cấp số cộng và cấp số nhân đầy đủ công thức quan trọng, lý thuyết và bài tập tự luyện giúp học sinh vận dụng và làm bài tập thật tốt môn Toán lớp 11.

• Các công thức về cấp số cộng

• Công thức tính công sai của cấp số cộng

• Công thức tìm số hạng tổng quát của cấp số cộng

• Công thức tính tổng n số hạng của cấp số cộng

• Các công thức về cấp số nhân

• Công thức tính công bội của cấp số nhân

• Công thức số hạng tổng quát của cấp số nhân

• Công thức tổng n số hạng tổng quát của cấp số nhân

---

---

---

Các công thức về cấp số cộng

1. Lý thuyết

a) Định nghĩa: (u_n) là cấp số cộng khi u_n+1 = u_n + d, n ∈ N^* (d gọi là công sai)

Nhận xét:

- Cấp số cộng (u_n) là một dãy số tăng khi và chỉ khi công sai d > 0. 

- Cấp số cộng (u_n) là một dãy số giảm khi và chỉ khi công sai d < 0. 

- Đặc biệt, khi d = 0 thì cấp số cộng là một dãy số không đổi (tất cả các số hạng đều bằng nhau). 

b) Số hạng tổng quát của cấp số cộng (u_n) được xác định bởi công thức: 

u_n = u₁ + (n – 1)d với n ∈ N^*, n ≥ 2.

c) Tính chất:

Ba số hạng u_k-1, u_k, u_k+1 (k ≥ 2) là ba số hạng liên tiếp của cấp số cộng khi và chỉ khi 

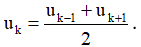
d) Tổng n số hạng đầu tiên S_n được xác định bởi công thức:

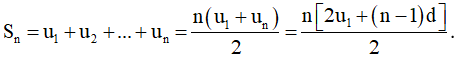
2. Công thức

- Công thức tính tính công sai: d = u_n+1 – u_n với n ∈ N^*.

- Công thức tìm số hạng tổng quát: u_n = u₁ + (n – 1)d với n ∈ N^*, n ≥ 2. 

- Tính chất của 3 số hạng u_k-1, u_k, u_k+1 (k ≥ 2) liên tiếp của cấp số cộng: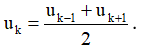

- Tổng n số hạng đầu tiên của cấp số cộng: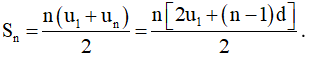

3. Ví dụ minh họa

Ví dụ 1: Cho cấp số cộng (u_n) thỏa mãn: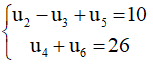  

a) Xác định công sai và số hạng đầu tiên của cấp số cộng.

b) Xác định công thức số hạng tổng quát của cấp số cộng.

c) Tính số hạng thứ 100 của cấp số cộng. 

d) Tính tổng 15 số hạng đầu tiên của cấp số cộng.

Lời giải

a) Gọi d là công sai của cấp số cộng, ta có: 

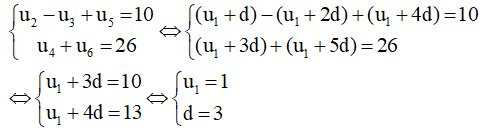
Vậy công sai d = 3 và số hạng đầu tiên u₁ = 1. 

b) Số hạng tổng quát: u_n = u₁ + (n – 1)d = 1 + (n – 1).3 = 3n – 2.

c) Số hạng thứ 100 là: u₁₀₀ = 3.100 – 2 = 298.

d) Tổng 15 số hạng đầu tiên: 

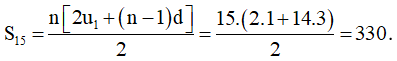
Ví dụ 2: Cho cấp số cộng (u_n) thỏa mãn: u_n = 2n – 3.

a) Xác định công sai của cấp số cộng

b) Số 393 là số hạng thứ bao nhiêu của cấp số cộng.

c) Tính S = u₁ + u₃ + u₅ + … + u₂₀₂₁

Lời giải

a) Ta có: u_{n + 1} = 2(n + 1) – 3 = 2n – 1

Công sai của cấp số cộng: d = u_n+1 – u_n = (2n – 1) – (2n – 3) = 2

b) Gọi số hạng thứ k của cấp số cộng là 393, ta có u_k = 393. 

Khi đó: 2k – 3 = 393. Suy ra k = 198.

Vậy số 393 là số hạng thứ 198 của cấp số cộng.

c) Ta có: u₁ = 2 . 1 – 3 = – 1

Dãy số là (v_n): u₁; u₃; u₅; … u₂₀₂₁ là cấp số cộng với số hạng đầu tiên là u₁ = – 1 và công sai d’ = u₃ – u₁ = 2d = 4

Dãy (v_n) có: (2021 – 1) : 2 + 1 = 1011 số hạng

Vậy tổng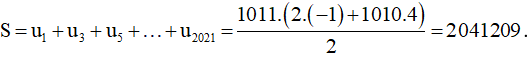 

Công thức tính công sai của cấp số cộng

1. Lý thuyết

Định nghĩa: (u_n) là cấp số cộng khi u_n+1 = u_n + d, n ∈ N^* (d gọi là công sai)

Công sai d của cấp số cộng là số không phụ thuộc vào n.

2. Công thức

- Tính công sai dựa vào định nghĩa: d = u_n+1 – u_n hoặc d = u₂ – u₁ = u₃ – u₂ = …

- Đề bài cho các dữ kiện khác: Lập hệ phương trình hai ẩn u₁ và d. Tìm u₁ và d.

3. Ví dụ minh họa

Ví dụ 1: 

a) Cho cấp số cộng (u_n) thỏa mãn: u_n+1 = u_n + 5. Tìm công sai của cấp số cộng.

b) Cho cấp số cộng (u_n) thỏa mãn: u_n+1 = – 3n + 5. Tìm công sai của cấp số cộng.

Lời giải

a) Công sai của cấp số cộng là: d = u_n+1 – u_n = 5.

b) Cách 1: Ta có: u_n = – 3(n – 1) + 5 = – 3n + 8

Công sai của cấp số cộng là: d = u_n+1 – u_n = (– 3n + 5) – (–3n + 8) = – 3.

Cách 2: Tính u₁ = – 3.0 + 5 = 5 và u₂ = – 3.1 + 5 = 2

Khi đó công sai của cấp số cộng: d = u₂ – u₁ = 2 – 5 = – 3.

Ví dụ 2: 

a) Cho cấp số cộng (u­_n) có u₄ = – 12 và u₁₄ = 18. Tìm u₁, d của cấp số cộng?

b) Cho cấp số cộng (u_n) thỏa mãn: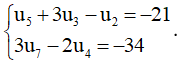

Tìm công sai của cấp số cộng.

Lời giải

a) Gọi d là công sai của cấp số cộng, ta có: 

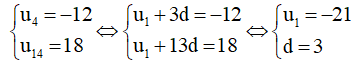
Vậy u₁ = – 21 và d = 3.

b) Gọi d là công sai của cấp số cộng, ta có: 

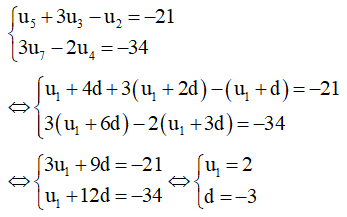
Vậy u₁ = 2 và d = – 3.

....................................

....................................

....................................

Trên đây là phần tóm tắt một số công thức Toán lớp 11 Chương 3: Dãy số - Cấp số cộng và cấp số nhân năm học 2021 - 2022 quan trọng, để xem chi tiết mời quí bạn đọc vào từng công thức trên!

Xem thêm các bài tổng hợp Công thức Toán lớp 11 đầy đủ, chi tiết khác:

• Chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song

---

---

---