Công thức Toán 9 quan trọng (mới)

Trọn bộ công thức Toán 9 chương trình mới Kết nối tri thức, Chân trời sáng tạo, Cánh diều đầy đủ Học kì 1, Học kì 2 Đại số và Hình học bao gồm các công thức quan trọng, lý thuyết và bài tập tự luyện giúp học sinh lớp 9 vận dụng để biết cách làm bài tập Toán 9.

Công thức Toán 9 quan trọng (mới)

Chủ đề: Phương trình và bất phương trình bậc nhất

• Công thức về tính chất bắc cầu của bất đẳng thức

• Công thức liên hệ giữa thứ tự và phép cộng

• Công thức liên hệ giữa thứ tự và phép nhân

Chủ đề: Căn bậc hai - Căn bậc ba

• Công thức về căn bậc hai và căn thức bậc hai

• Công thức liên hệ giữa phép khai căn bậc hai và phép nhân

• Công thức liên hệ giữa phép khai căn bậc hai và phép chia

• Công thức đưa thừa số ra ngoài dấu căn

• Công thức đưa thừa số vào trong dấu căn

• Công thức về căn bậc hai và căn thức bậc ba

• Công thức trục căn thức ở mẫu

• Công thức căn bậc hai

• Các hằng đẳng thức căn bậc hai

• Các công thức biến đổi căn bậc hai

• Công thức căn bậc 3

• Công thức giải phương trình chứa căn

• Hằng đẳng thức căn bậc ba

Chủ đề: Hàm số y = ax² (a ≠ 0). Phương trình bậc hai một ẩn

• Công thức nghiệm và công thức nghiệm thu gọn của phương trình bậc hai một ẩn

• Định lí Viète cho phương trình bậc hai một ẩn

• Công thức nhẩm nghiệm của phương trình bậc hai một ẩn

• Công thức viết phương trình bậc hai một ẩn khi biết tổng và tích hai nghiệm của chúng

Chủ đề: Hệ thức lượng trong tam giác vuông

• Công thức tỉ số lượng giác của góc nhọn

• Công thức tỉ số lượng giác của hai góc phụ nhau

• Công thức liên hệ giữa cạnh huyền và cạnh góc vuông

• Công thức liên hệ giữa hai cạnh góc vuông

• Công thức Hệ thức lượng trong tam giác vuông

• Công thức Tỉ số lượng giác của góc nhọn

• Công thức tính diện tích tam giác

Chủ đề: Hàm số bậc nhất

• Công thức xét tính đồng biến, nghịch biến của hàm số hay, chi tiết

• Cách vẽ đồ thị hàm số bậc nhất hay, chi tiết

• Công thức về hệ số góc của đường thẳng hay, chi tiết

• Công thức về vị trí tương đối của hai đường thẳng đầy đủ, chi tiết

• Công thức tìm tọa độ giao điểm của hai đường thẳng hay, chi tiết

Chủ đề: Đường tròn

• Công thức tính góc ở tâm và số đo của một cung

• Công thức tính số đo góc nội tiếp của đường tròn

• Công thức tính độ dài của cung tròn

• Công thức tính diện tích hình quạt tròn và hình vành khuyên

• Công thức liên hệ giữa đường nối tâm và tâm của hai đường tròn

• Công thức liên hệ đường kính và dây cung đầy đủ, chi tiết

• Công thức liên hệ giữa dây và khoảng cách từ tâm đến dây hay, chi tiết

• Vị trí tương đối của đường thẳng và đường tròn đầy đủ, chi tiết

• Vị trí tương đối của hai đường tròn đầy đủ, chi tiết

• Tính chất hai tiếp tuyến cắt nhau đầy đủ, chi tiết

Chủ đề: Đường tròn ngoại tiếp và đường tròn nội tiếp. Đa giác đều

• Công thức tính bán kính đường tròn ngoại tiếp tam giác vuông

• Công thức tính bán kính đường tròn ngoại tiếp và bán kính đường tròn nội tiếp của tam giác đều

• Công thức tính bán kính đường tròn ngoại tiếp của hình chữ nhật và hình vuông

• Tổng số đo hai góc đối nhau của một tứ giác nội tiếp

• Công thức tìm góc quay của phép quay giữ nguyên hình đa giác đều

Chủ đề: Hình học trực quan

• Công thức tính diện tích xung quanh và thể tích của hình trụ

• Công thức tính diện tích xung quanh và thể tích của hình nón

• Công thức tính diện tích mặt cầu và thể tích của hình cầu

Chủ đề: Một số yếu tố thống kê và xác xuất

• Công thức tính tần số tương đối và tần số tương đối ghép nhóm

• Công thức tính xác suất của biến cố liên quan tới phép thử

---

---

---

Công thức căn bậc hai

I. Lý thuyết

+ Căn bậc hai của một số thực a không âm là x sao cho x² = a 

+ Mỗi số dương a có hai căn bậc hai là √a và -√a ; 

+ Số 0 có một căn bậc hai là 0 

+ Số âm không có căn bậc hai.

Chú ý: Căn bậc hai số học của một số a không âm là √a 

 

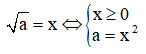
II. Các công thức:

1. Điều kiện để căn thức, biểu thức có nghĩa

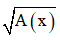+  có nghĩa khi A ( x ) ≥ 0

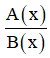+  có nghĩa khi B ( x ) ≠ 0

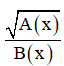+ có nghĩa khi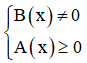  

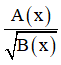+  có nghĩa khi B ( x ) > 0

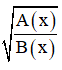+ có nghĩa khi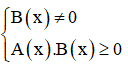  

2. So sánh căn bậc hai

 a > b ≥ 0 => √a > √b

                             

III. Các ví dụ

Ví dụ 1:Tìm căn bậc hai của các số sau đây:

a) 25

b)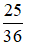  

Lời giải:

a) Căn bậc hai của 25 là 5 và -5 vì 5² = 25 và (-5)² = 25

b) Căn bậc hai của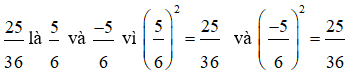

Ví dụ 2: Tìm điều kiện của x để căn sau có nghĩa:

 

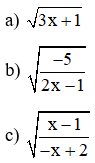
Lời giải:

a) 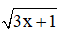 có nghĩa

 ⇔ 3x + 1 ≥ 0 

⇔ 3x ≥ -1

⇔ x ≥ -1 : 3

⇔ x ≥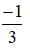

Vậy 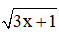có nghĩa khi x ≥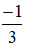

b) Ta có để 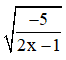 có nghĩa

⇔  

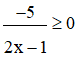
Vì –5 < 0 nên để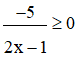  

thì 2x - 1 < 0 (do mẫu số phải khác 0 nên 2x - 1 ≠ 0 )

2x - 1 < 0

⇔ 2x < 1 

⇔ x <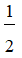

Vậy x < 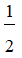 thì căn có nghĩa

c) Để 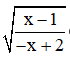 có nghĩa thì

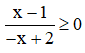 . Ta có hai trường hợp:

Trường hợp 1:

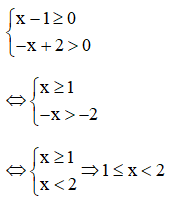
Trường hợp 2:

 

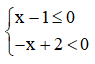
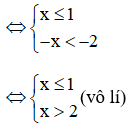
Vậy để 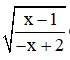 có nghĩa thì 1 ≤ x < 2

Ví dụ 3: So sánh các căn bậc hai sau: 

a) 5 và 2√5                                                                     

b) 4 và √17 + 1 

Lời giải:

a) Ta có: 5² = 25 và (2√5)² = 2².5 = 4.5 = 20

Vì 25 > 20 nên √25 > √20 

=> 5 > 2√5

b) Ta có: 4 = 3 + 1 vậy để so sánh 4 và √17 + 1  ta đi so sánh 3 và √17

 3² = 9. Vì 17 > 9 nên √17 > √9 => √17 > 3 => √17 + 1 > 3 + 1 => √17 + 1 > 4    

IV. Bài tập tự luyện

Bài 1: Tìm căn bậc hai, căn bậc hai số học của các số sau đây

4; 1,69; 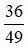 ; 64    

Bài 2: Tìm điều kiện để căn có nghĩa:

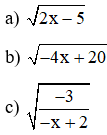
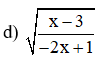
Bài 3: So sánh các số sau: 

a) √51 và 7

b) 3√23 và 2√31 

c) √11 + 1 và 4

....................................

....................................

....................................

Công thức Hệ thức lượng trong tam giác vuông

I. Lý thuyết

Cho tam giác ABC vuông tại A đường cao AH

Ta kí hiệu:

AB = c; BC = a; AC = b; AH = h; BH = c’; CH = b’

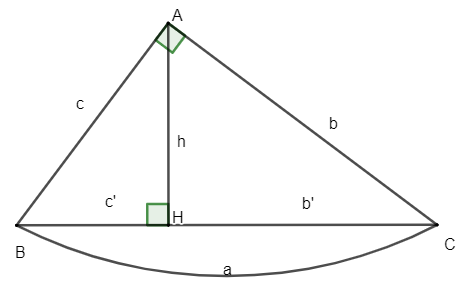
Khi đó ta có các hệ thức sau:

+ AB² = BH.BC hay c² = a.c^'

+ AC² = CH.BC hay b² = a.b^'

+ AH² = BH.CH hay h² = b^'.c^' 

+ AB.AC = AH.BC hay b.c = a.h 

+

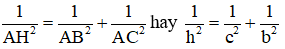
+ AB² + AC² = BC² hay c² + b² = c² (định lý Py – ta – go)

II. Bài tập 

Bài 1: Tìm x, y trong hình vẽ:

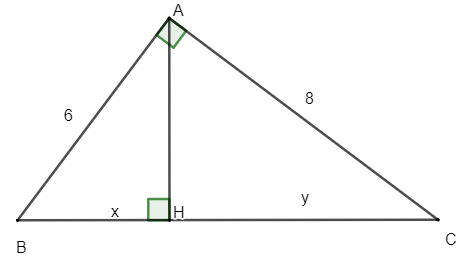
Lời giải:

Áp dụng định lý Py – ta – go cho tam giác vuông ABC ta có:

 AB² + AC² = BC²

⇔ 6² + 8² = BC²

⇔ BC² = 100²

⇔ BC = 10

Với AH là đường cao, áp dụng hệ thức lượng cho tam giác vuông ABC ta có:

AB² = BH.BC

⇔ 6² = BH.10

⇔ 36 = BH.10

⇔ BH = 36 : 10

⇔ BH = 3,6

Tương tự ta có:

AC² = CH.BC

⇔ 8² = CH.10

⇔ 64 = CH.10

⇔ CH = 64 : 10

⇔ CH = 6,4

Bài 2: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB : AC = 3: 4 và BC=15. Tính BH, CH.

Lời giải:

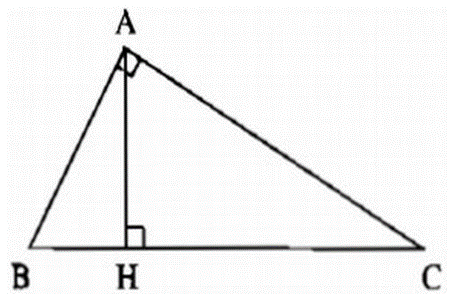
Ta có: AB : AC = 3 : 4

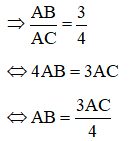
Áp dụng định lý Py – ta – go cho tam giác ABC vuông tại A ta có:

AB² + AC² = BC²

Thay BC = 15; 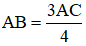 ta có:

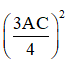+ AC² = 15²

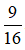⇔ AC² + AC² = 225

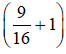⇔ AC² = 225

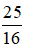⇔ AC² = 225

⇔ AC² = 225 :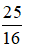 

⇔ AC² = 144

⇔ AC = 12

Áp dụng hệ thức lượng cho tam giác ABC vuông tại A đường cao AH ta có:

AB² = BH.BC

⇔ 12²= CH.15

⇔ CH = 144 : 15

⇔ CH = 9,6

=> BH = BC – CH = 15 – 9,6 = 5,4

Công thức Tỉ số lượng giác của góc nhọn

I. Lý thuyết

1. Định nghĩa

Cho góc nhọn α (0^o < α < 90^o ). Dựng tam giác ABC vuông tại A sao cho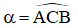

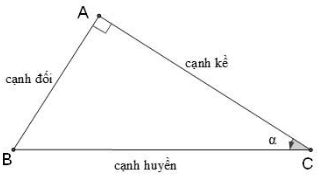
AB là cạnh đối của góc α

AC là cạnh kề của góc α

BC là cạnh huyền

Khi đó ta có các tỉ số lượng giác sau:

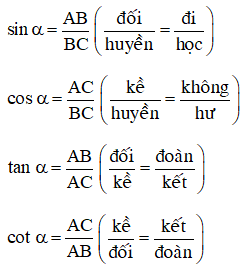
2. Tính chất

+ Với góc nhọn α bất kỳ ta có:

0 < sin α < 1

0 < cos α < 1

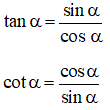
tan α.cot α = 1

sin²α + cos²α = 1

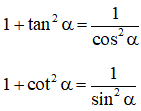
+ Nếu α + β = 90^o 

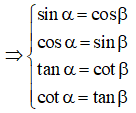
+ Nếu góc α tăng 0^o từ đến 90^o thì sin α tăng dần, cos α giảm dần.

3. Bảng tỉ số lượng giác một số góc đặc biệt

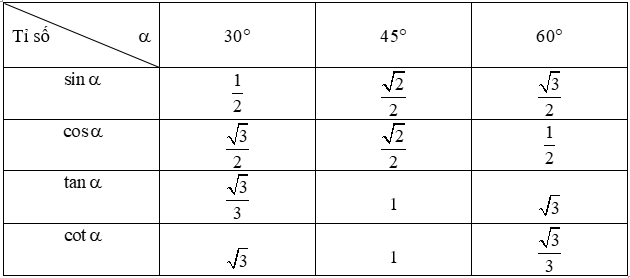
4. So sánh hai góc nhọn α,β

+ sin α < sin β ⇔ α < β

+ cos α < cos β ⇔ α > β

+ tan α < tan β ⇔ α < β

+ cot α < cot β ⇔ α > β

5. Công thức tính các cạnh tam giác.

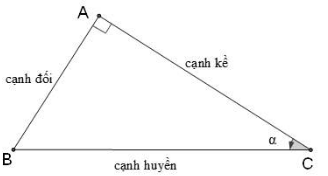
Với AB = c; AC = b; BC = a ta có các công thức:

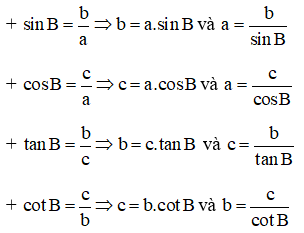
II. Bài tập

Bài 1: Cho tam giác ABC vuông tại C có BC = 0,9 cm, AC = 1,2 cm. Tính các tỉ số lượng giác của góc B. Từ đó suy ra tỉ số lượng giác của góc A

Lời giải:

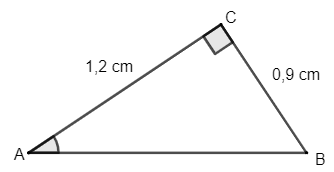
Áp dụng định lý Py – ta – go cho tam giác vuông ABC ta có:

AC² + BC² = AB²

⇔ 1,2² + 0,9² = AB²

⇔ 1,44 +  0,81 = AB²

⇔ 2,25 = AB²

=> AB = 1,5cm

Tỉ số lượng giác góc A là:

..........................

..........................

..........................

Trên đây là tóm lược một số nội dung có trong tổng hợp công thức Toán lớp 9 Học kì 1 và Học kì 2, mời quí bạn đọc vào từng bài để xem đầy đủ, chi tiết!

---