Giải Toán 12 trang 79 Tập 2 Cánh diều
Với Giải Toán 12 trang 79 Tập 2 trong Bài 2: Phương trình đường thẳng Toán 12 Tập 2 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 79.
Giải Toán 12 trang 79 Tập 2 Cánh diều
Bài 6 trang 79 Toán 12 Tập 2: Xác định vị trí tương đối của hai đường thẳng ∆1, ∆2 trong mỗi trường hợp sau:
Lời giải:
a) Đường thẳng ∆1 đi qua điểm M1(1; 2; 3) và có là vectơ chỉ phương.
Đường thẳng ∆2 đi qua điểm M2(– 11; – 6; 10) và có là vectơ chỉ phương.
Ta có, suy ra , cùng phương;
và nên không cùng phương.
Vậy ∆1 // ∆2.
b) Đường thẳng ∆1 đi qua điểm M1(1; 2; 3) và có là vectơ chỉ phương.
Đường thẳng ∆2 đi qua điểm M2(– 3; – 6; 15) và có là vectơ chỉ phương.
Ta có:, suy ra , không cùng phương;
, .
Do (– 22) ∙ (– 4) + 14 ∙ (– 8) + 2 ∙ 12 = 0 nên đồng phẳng.
Vậy ∆1 cắt ∆2.
c) Đường thẳng ∆1 đi qua điểm M1(– 1; 1; 0) và có là vectơ chỉ phương.
Đường thẳng ∆2 đi qua điểm M2(1; 3; 1) và có là vectơ chỉ phương.
Ta có: ,.
Do 4 ∙ 2 + (– 7) ∙ 2 + 5 ∙ 1 = – 1 ≠ 0 nên không đồng phẳng.
Vậy ∆1 và ∆2 chéo nhau.
Bài 7 trang 79 Toán 12 Tập 2: Tính góc giữa hai đường thẳng ∆1, ∆2 trong mỗi trường hợp sau (làm tròn kết quả đến hàng đơn vị của độ):
Lời giải:
a) Hai đường thẳng ∆1 và ∆2 có vectơ chỉ phương lần lượt là ,.
Ta có: cos (∆1, ∆2) = .
Suy ra (∆1, ∆2) = 30°.
b) Hai đường thẳng ∆1 và ∆2 có vectơ chỉ phương lần lượt là , .
Ta có: cos (∆1, ∆2) = .
Suy ra (∆1, ∆2) ≈ 11°.
c) Hai đường thẳng ∆1 và ∆2 có vectơ chỉ phương lần lượt là và .
Ta có: cos (∆1, ∆2) = .
Suy ra (∆1, ∆2) ≈ 80°.
Bài 8 trang 79 Toán 12 Tập 2: Tính góc giữa đường thẳng ∆ và mặt phẳng (P) trong mỗi trường hợp sau (làm tròn kết quả đến hàng đơn vị của độ):
a) (t là tham số) và (P):x + z – 2 = 0;
b) (t là tham số) và (P): x + y + z – 4 = 0.
Lời giải:
a) Đường thẳng ∆ có vectơ chỉ phương là và mặt phẳng (P) có vectơ pháp tuyến là . Ta thấy vectơ chỉ phương của ∆ đồng thời là vectơ pháp tuyến của (P), do đó ∆ ⊥ (P), suy ra (∆, (P)) = 90°.
b) Đường thẳng ∆ có vectơ chỉ phương là và mặt phẳng (P) có vectơ pháp tuyến là .
Ta có sin (∆, (P)) = .
Suy ra (∆, (P)) ≈ 19°.
Bài 9 trang 79 Toán 12 Tập 2: Tính góc giữa hai mặt phẳng
(P1): x + y + 2z – 1 = 0 và (P2): 2x – y + z – 2 = 0.
Lời giải:
Do (P1), (P2) có hai vectơ pháp tuyến lần lượt là , nên
cos ((P1), (P2)) = .
Suy ra ((P1), (P2)) = 60°.
Lời giải bài tập Toán 12 Bài 2: Phương trình đường thẳng hay khác:
- Giải Toán 12 trang 65
- Giải Toán 12 trang 67
- Giải Toán 12 trang 68
- Giải Toán 12 trang 69
- Giải Toán 12 trang 73
- Giải Toán 12 trang 74
- Giải Toán 12 trang 75
- Giải Toán 12 trang 78
- Giải Toán 12 trang 80
Xem thêm lời giải bài tập Toán lớp 12 Cánh diều hay, chi tiết khác:
Xem thêm các tài liệu học tốt lớp 12 hay khác:
- Giải sgk Toán 12 Cánh diều
- Giải Chuyên đề học tập Toán 12 Cánh diều
- Giải SBT Toán 12 Cánh diều
- Giải lớp 12 Cánh diều (các môn học)
- Giải lớp 12 Kết nối tri thức (các môn học)
- Giải lớp 12 Chân trời sáng tạo (các môn học)
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Soạn văn 12 Cánh diều (hay nhất)
- Soạn văn 12 Cánh diều (ngắn nhất)
- Giải sgk Toán 12 Cánh diều
- Giải Tiếng Anh 12 Global Success
- Giải sgk Tiếng Anh 12 Smart World
- Giải sgk Tiếng Anh 12 Friends Global
- Giải sgk Vật Lí 12 - Cánh diều
- Giải sgk Hóa học 12 - Cánh diều
- Giải sgk Sinh học 12 - Cánh diều
- Giải sgk Lịch Sử 12 - Cánh diều
- Giải sgk Địa Lí 12 - Cánh diều
- Giải sgk Giáo dục KTPL 12 - Cánh diều
- Giải sgk Tin học 12 - Cánh diều
- Giải sgk Công nghệ 12 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 12 - Cánh diều
- Giải sgk Giáo dục quốc phòng 12 - Cánh diều
- Giải sgk Âm nhạc 12 - Cánh diều

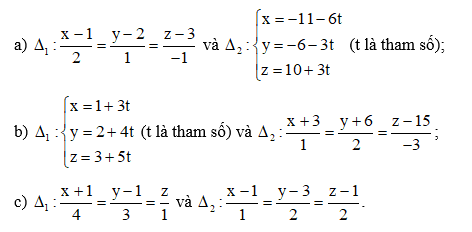
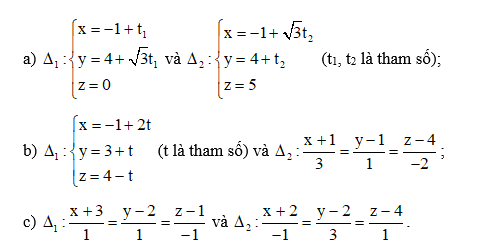



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

