60 bài tập trắc nghiệm Xác suất chọn lọc, có lời giải (phần 2)
Với 60 bài tập trắc nghiệm Xác suất (phần 2) có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm bài tập trắc nghiệm Xác suất (phần 2).
60 bài tập trắc nghiệm Xác suất chọn lọc, có lời giải (phần 2)
(199k) Xem Khóa học Toán 11 KNTTXem Khóa học Toán 11 CDXem Khóa học Toán 11 CTST
Bài 1: Trong một bài thi trắc nghiệm khách quan có 20 câu, mỗi câu có 4 phương án trả lời trong đó chỉ có 1 phương án đúng. Một học sinh không học bài nên làm bài bài bằng cách chọn ngẫu nhiên mỗi câu một phương án. Tính xác suất để học sinh đó trả lời đúng 10 câu?
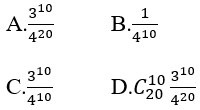
Lời giải:
Đáp án: D
Gọi Ai là biến cố:" học sinh chọn đúng ở câu i" i= 1,2,..,20
Ta có P(Ai) =1/4, thì 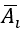
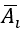
Gọi X là biến cố:" Học sinh trả lời đúng 10 câu trong 20 câu"
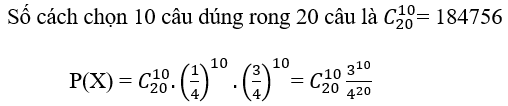
Bài 2: Có hai hộp bút chì. Hộp 1 có 3 bút đỏ và 4 bút xanh. Hộp II có 8 bút đỏ và 4 bút xanh. Chọn ngẫu nhiên từ mỗi hộp ra 1 bút. Tính xác suất để có 1 bút đỏ và 1 bút xanh.
A.1/12 B.1/6 C.7/12 D.11/24
Lời giải:
Đáp án: C
Gọi A là biến cố:" chọn bút đỏ ở hộ thứ i" i=1,2
B là biến cố:" chọn bút xanh ở hộp thứ i " i= 1,2
Ta có P(A1)=3/12; P(A2)=8/12 ; P(B1) =9/12; P(B2) =4/12
Gọi X là biến cố: " chọn được 1 bút đỏ và 1 bút xanh" thì X= A1B2∪ A2 B1
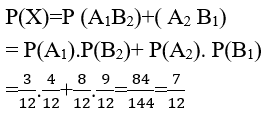
Bài 3: Một nhóm bạn có 4 bạn gồm 2 bạn Mạnh, Dũng và hai nữ là Hoa, Lan được xếp ngẫu nhiên trên một ghế dài. Kí hiệu (MDHL) là cách sắp xếp theo thứ tự: Mạnh, Dũng, Hoa, Lan
Tính số phần tử của không gian mẫu
A. 6 B. 24 C. 1 D. 4
Lời giải:
Đáp án: B
Mỗi cách xắp sêp 4 bạn vào 4 chỗ ngồi là một hoán vị của 4 phần tử. Vì vậy số phần tử của không gian mẫu là 4! =24
Bài 4: Một nhóm bạn có 4 bạn gồm 2 bạn Mạnh, Dũng và hai nữ là Hoa, Lan được xếp ngẫu nhiên trên một ghế dài. Kí hiệu (MDHL) là cách sắp xếp theo thứ tự: Mạnh, Dũng, Hoa, Lan
Xác định biến cố M:"xếp hai nam ngồi cạnh nhau"
A. M={(MDHL),(HMDL),(HLMD)}
B. M={(MDHL),(LMDH),(LHMD)}
C. M={(MDHL),(MDLH),(HMDL),(LMDH),(HLMD),(LHMD)}
D. M={(MDHL),(DMHL),(MDLH),(DMLH),(HMDL),(HDML),(LMDH),(LDMH),(HLMD),(HLDM),(LHMD),(LHDM)}
Lời giải:
Đáp án: D
Đánh số ghế theo thứ tự 1,2,3,4. Hai bạn nam ngồi cạnh nhau ở vị trí ( 1 và 2) hoặc (2 và 3) hoặc (3 và 4). Nếu hai bạn nam đổi chỗ cho nhau( giữ nguyên chỗ hai bạn nữ) thì ta có một cách xếp mới . Vì vậy cần chọn phương án D
Bài 5: Một nhóm bạn có 4 bạn gồm 2 bạn Mạnh, Dũng và hai nữ là Hoa, Lan được xếp ngẫu nhiên trên một ghế dài. Kí hiệu (MDHL) là cách sắp xếp theo thứ tự: Mạnh, Dũng, Hoa, Lan
Tìm số phần tử của biến cố N:"xếp nam và nữ ngồi xen kẽ nhau"
A.24 B.4 C.8 D.6
Lời giải:
Đáp án: C
Trường hợp 1: bạn nam ngồi đầu. khi dó 2 bạn nam xếp vào 2 chỗ ( số ghế 1 và 3), nữ xếp nốt vào hai chỗ còn lại ( ghế số 2 và 4), số cách xếp là 2!.2!=4
Trường hợp 2: bnạ nữ ngồi đầu. Tương tự có 4 cách xếp . Vậy theo quy tắc cộng số phần tử của biến cố N là 4+4=8
Bài 6: Gieo ngẫu nhiên ba đồng xu phân biệt một lần. Kí hiệu S, N lần lượt chỉ đồng xu lật sấp, lật ngửa
Hãy mô tả không gian mẫu
A.Ω={S,N,S}
B.Ω={SSS,SSN,SNS,NSS}
C.Ω={SSS,SSN,SNS,NSS,NNS,NSN,SNN,NNN}
D.Ω={NNN,NSN,SNS}
Lời giải:
Đáp án: C
Mỗi phần tử của không gian mẫu chỉ rõ ba đồng tiền xuất hiện ngẫu nhiên mặt sấp hay mặt ngửa. Vì vậy cần chọn phương án C
Bài 7: Chọn ngẫu nhiên 5 sản phẩm trong 10 sản phẩm. Biết rằng trong 10 sản phẩm đó có 2 phế phẩm.
Tính xác suất để trong 5 sản phẩm được chọn đó không có phế phẩm nào:
A.1/2 B.5/8 C.2/9 D.1/5
Lời giải:
Đáp án: C
Số khả năng chọn 5 sản phẩm trong 10 sản phẩm là
Gọi A là biến cố:" trong 5 sản phẩm được chọn không có phế phẩm nào"
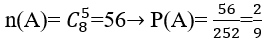
Bài 8: Chọn ngẫu nhiên 5 sản phẩm trong 10 sản phẩm. Biết rằng trong 10 sản phẩm đó có 2 phế phẩm. Tính xác suất để trong 5 sản phẩm được chọn có ít nhất 1 phế phẩm
A.1/2 B.3/8 C.7/9 D.4/5
Lời giải:
Đáp án: D
Gọi B là biến cố:" trong 5 sản phẩm được chọn có ít nhất 1 phế phẩm" thì
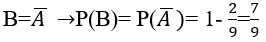
Bài 9: Một hộp có 5 viên bi đỏ và 9 viên bi xanh. Chọn ngẫu nhiên 2 viên bi. Xác suất để chọn được 2 viên bi khác màu là:
A. 14/35. B. 45/91. C. 46/91. D. 15/22.
Lời giải:
Đáp án: B
Chọn B.
Gọi A là biến cố: "chọn được 2 viên bi khác màu."
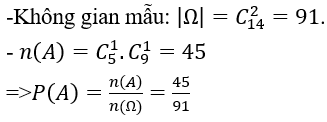
Bài 10: Một hộp chứa ba quả cầu trắng và hai quả cầu đen. Lấy ngẫu nhiên đồng thời hai quả. Xác suất để lấy được cả hai quả trắng là:
A. 2/10 B. 3/10 C. 4/10 D. 5/10
Lời giải:
Đáp án: B
Chọn B.
Gọi A là biến cố: "lấy được cả hai quả trắng."
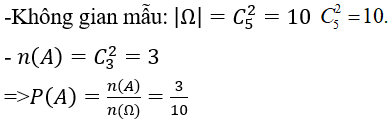
Bài 11: Có hai hộp thẻ. Hộp thứ nhất chứa các thẻ được đánh số từ 1 đến 5, hộp thứ hai chứa các thẻ được đánh số từ 6 đến 9. Lấy ngẫu nhiên ở mỗi hợp 1 thẻ
Hãy mô tả không gian mẫu, kí hiệu "ab" thể hiện hộp thứ nhất lấy thể đánh số a, hộp thứ hai lấy thẻ đánh số b.
A. Ω={16,27,38,49,56}
B. Ω={19,28,37,46,57}
C. Ω={16,17,18,19,26,27,28,29,36,37,38,39,46,47,48,49,56,57,58,59}
D. Ω={61,62,63,64,65,71,72,73,74,75,81,82,83,84,85,91,92,92,94,95}
Lời giải:
Đáp án: C
Ω={16,17,18,19,26,27,28,29,36,37,38,39,46,47,48,49,56,57,58,59}
Vì hộp thứ nhất chứa các thẻ được đánh số từ 1 đến 5, hộp thứ hai chứa các thẻ được đánh số từ 6 đến 9
Bài 12: Có hai hộp thẻ. Hộp thứ nhất chứa các thẻ được đánh số từ 1 đến 5, hộp thứ hai chứa các thẻ được đánh số từ 6 đến 9. Lấy ngẫu nhiên ở mỗi hợp 1 thẻ
Xác định biến cố M:"tổng các số ở hai thẻ lấy ra là số nguyên tố"
A. M={16,38,49,56}
B. M={16,29,38,47,49,56,58}
C. M={61,74,92,94,65}
D. M={16,38,56}
Lời giải:
Đáp án: B
M={16,29,38,47,49,56,58} tổng các chữ số là số nguyên tố
Bài 13: Có ba xạ thủ đi săn đêm. Gọi Ak là biến cố:"xạ thủ thứ k bắn trúng đích" với k = 1,2,3. Hãy dùng các phép toán nêu các biến cố biểu thị qua A1,A2,A3.
Biến cố M: "không có xạ thủ nào bắn trúng đích"
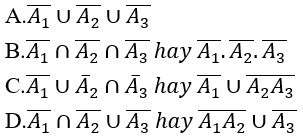
Lời giải:
Đáp án: B
Theo bài ra biến cố Ak: " xạ thủ thứ k bắn trúng đích ", với k=1,2,3 thì biến cố đối 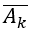
Biến cố M " không có xạ thủ nào bắn trúng đích" , tức là cả ba xạ thủ đều bắn trượt nên
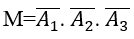
Bài 14: Có ba xạ thủ đi săn đêm. Gọi Ak là biến cố:"xạ thủ thứ k bắn trúng đích" với k = 1,2,3. Hãy dùng các phép toán nêu các biến cố biểu thị qua A1,A2,A3.
Biến cố N:"có đúng hai xạ thủ trúng đích"
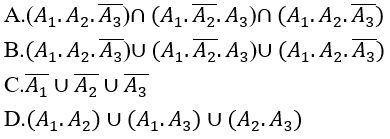
Lời giải:
Đáp án: B
Biến cố N: " có đúng hai xạ thủ bắn trúng đích" tức là trong ba xạ thủ có hai người bắn trúng và một người bắn trượt
Bài 15: Gieo hai con súc sắc. Xác suất để tổng số chấm trên hai mặt chia hết cho 3 là:
A. 13/36 B. 11/36. C. 1/3. D. 1/6.
Lời giải:
Đáp án: C
Chọn C.
Số phần tử không gian mẫu:n(Ω)=6.6=36
Biến cố tổng hai mặt chia hết cho là:
A={(1,2);(1,5);(2,1);(2,4);(3,3);(3,6);(4,2);(4,5);(5,1);(5,4);(6,3);(6,6)}
Nên n(A)=12
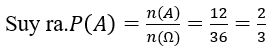
Bài 16: Gieo ba con súc sắc. Xác suất để nhiều nhất hai mặt 5 là:
A. 5/72. B. 1/216 C. 1/72. D.1
Lời giải:
Đáp án: D
Chọn D.
Số phần tử không gian mẫu: n(Ω)=6.6.6=216
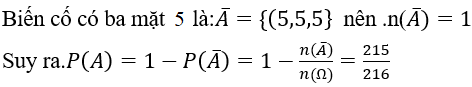
Bài 17: Rút ra một lá bài từ bộ bài 52 lá. Xác suất để được lá át (A) là:
A. 2/13. B. 1/169. C. 1/13. D. 3/4 .
Lời giải:
Đáp án: C
Chọn C.
Số phần tử không gian mẫu: : n(Ω)=52
Số phần tử của biến cố xuất hiện lá ách: : n(A)=4
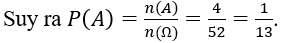
Bài 18: Rút ra một lá bài từ bộ bài 52 lá. Xác suất để được lá ách (A) hay lá rô là:
A. 1/52. B. 2/13. C. 4/13. D. 17/52.
Lời giải:
Đáp án: C
Chọn C.
Số phần tử không gian mẫu: : n(Ω)=52
Số phần tử của biến cố xuất hiện lá ách: : n(A)=4
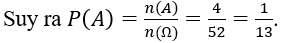
Bài 19: Gieo hai đồng tiền một lần. Kí hiệu S,N để chỉ đông tiền lật sấp, lật ngửa.
Mô tả không gian mẫu
A. Ω={SN,NS}
B. Ω={NN,SS}
C. Ω={S,N}
D. Ω={SN,NS,SS,NN}
Lời giải:
Đáp án: D
Ω={SN,NS,SS,NN}
Bài 20: Gieo hai đồng tiền một lần. Kí hiệu S,N để chỉ đông tiền lật sấp, lật ngửa.
Xác định biến cố M: "hai đông tiền xuất hiện hai mặt không giống nhau"
A. M={NN,SS}
B. M={NS,SN}
C. M={NS,NN}
D. M={SS,SN}
Lời giải:
Đáp án: B
M={NS,SN}
Bài 21: Một chiếc máy có ba động cơ I,II,III hoạt động độc lập với nhau. Xác xuất để động cơ I,II,III chạy tốt tương ứng là 0,7;0,8;0,9.
Xác suất để cả 3 động cơ chạy tốt
A.0.006
B.0.496
C.0.504
D.0.994
Lời giải:
Đáp án: D
Gọi Ai là biến cố:" động cơ i chạy tốt" i=1,2,3
P(A1)= 0,7 ; P(A2).= 0,8 ; P(A3)=0,9 và A1, A2, A3 độc lập với nhau
A1, A2, A3 là biến cố:" cả 3 biến cố đều chạy tốt "
P(A1. A2. A3)= P(A1). P(A2). P(A3)= 0,504
Bài 22: Một bộ bài tú lơ khơ gồm 53 con, lấy ngẫu nhiên lần lượt có hoàn lại từng con cho đến khi lần đầu tiên lấy được con át thì dừng
Tính xác suất sao cho quá trình dừng lại ở ngay lần thứ nhất
A.12/13 B.1/13 C.1/4 D.0
Lời giải:
Đáp án: B
Kí hiệu Ak: " lần thứ k lấy được con át" k ≥ 1

Bài 23: Trong một buổi liên hoan có 6 cặp nam nữ, trong đó có 3 cặp là vợ chồng. Chọn ngẫu nhiên 3 người trong số đó tham gia trò chơi
Tính xác suất để trong 3 người dược chọn không có cặp vợ chồng nào
A.1/4 B.9/22 C.1/11 D.19/22
Lời giải:
Đáp án: D
Gọi B là biến cố :" trong 3 người được chọn không có cặp vợ chồng nào" thì 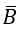
Ta có n(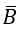
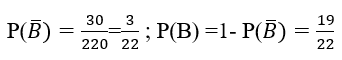
Bài 24: Một lớp học có 40 học sinh trong đó coa 15 học sinh giỏi Toán, 10 học sinh giỏi Văn và 5 học sinh giỏi cả Văn và Toán. Chọn ngẫu nhiên một học sinh.
Xác suất của biến cố A:"học sinh được chọn giỏi Toán" là:
A.1/40 B.8/3 C.3/8 D.1/8
Lời giải:
Đáp án: C
Ta có n(Ω) = 40
Rõ ràng n(A) = 15 nên P(A) = 15/40 = 3/8
Chọn đáp án là C
Bài 25: Lấy ngẫu nhiên 1 thẻ từ 1 hộp 30 thẻ được đánh số từ 1 đến 30.
Tính xác suất để thẻ được lấy ghi số 6
A.1/30 B.1/5 C.6 D.1/6
Lời giải:
Đáp án: A
không gian mẫu Ω={1,2,..30}. kí hiệu A là biến cố " thẻ lấy ra ghi số 6", B là biến cố "thẻ lấy ra ghi số chia hết cho 5"
A={6}, n(A) =1,n(Ω) = 30
⇒ P(A) =1/30
Chọn đáp án A
Bài 26: Trong một buổi liên hoan có 6 cặp nam nữ, trong đó có 3 cặp là vợ chồng. Chọn ngẫu nhiên 3 người trong số đó tham gia trò chơi
Tính xác suất để trong 3 người được chọn có đúng 1 người là nam
A. 1/4 B. 9/22 C. 1/11 D. 19/22
Lời giải:
Đáp án: B
Số khả năng chọn ngẫu nhiên 3 người từ 6*2= 12 người là
a. Gọi A là biến cố:" trong 3 người được chọn có đúng 1 nam"
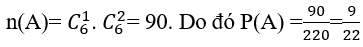
Bài 27: Một hộp chứa ba quả cầu trắng và hai quả cầu đen. Lấy ngẫu nhiên đồng thời hai quả. Xác suất để lấy được cả hai quả trắng là:
A. 2/10 B. 3/10 C. 4/10 D. 5/10
Lời giải:
Đáp án: B
Chọn B.
Gọi A là biến cố: "lấy được cả hai quả trắng."
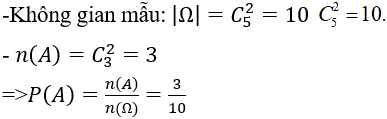
Bài 28: Một túi chứa 2 bi trắng và 3 bi đen. Rút ra 3 bi. Xác suất để được ít nhất 1 bi trắng là:
A. 1/5. B. 1/10. C. 9/10. D. 4/5.
Lời giải:
Đáp án: C
Số phần tử của không gian mẫu: n(Ω)=10
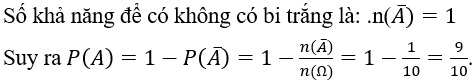
Bài 29: Từ ác chữ số 1,2,3,4 nhười ta lập các số tự nhiên có 3 chữ số khác nhau. Tính số phần tử không gian mẫu
A. 16 B. 24 C. 6 D. 4
Lời giải:
Đáp án: B
Ta lập được 4!=24 số
Bài 30: Trong một buổi liên hoan có 6 cặp nam nữ, trong đó có 3 cặp là vợ chồng. Chọn ngẫu nhiên 3 người trong số đó tham gia trò chơi
Tính xác suất để trong 3 người dược chọn không có cặp vợ chồng nào
A. 1/4 B. 9/22 C. 1/11 D. 19/22
Lời giải:
Đáp án: D
Gọi B là biến cố :" trong 3 người được chọn không có cặp vợ chồng nào" thì 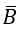
Ta có n(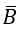
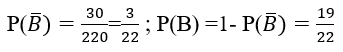
(199k) Xem Khóa học Toán 11 KNTTXem Khóa học Toán 11 CDXem Khóa học Toán 11 CTST
Xem thêm các dạng bài tập Toán lớp 11 có trong đề thi THPT Quốc gia khác:
- Dạng 1: Xác định phép thử, không gian mẫu và biến cố
- Trắc nghiệm xác định phép thử, không gian mẫu và biến cố
- Dạng 2: Tính xác suất theo định nghĩa cổ điển
- Trắc nghiệm tính xác suất theo định nghĩa cổ điển
- Dạng 3: Các quy tắc tính xác suất
- Trắc nghiệm các quy tắc tính xác suất
- 60 bài tập trắc nghiệm Xác suất chọn lọc, có lời giải (phần 1)
Tủ sách VIETJACK shopee lớp 10-11 (cả 3 bộ sách):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 11 Global Success
- Giải sgk Tiếng Anh 11 Smart World
- Giải sgk Tiếng Anh 11 Friends Global
- Lớp 11 - Kết nối tri thức
- Soạn văn 11 (hay nhất) - KNTT
- Soạn văn 11 (ngắn nhất) - KNTT
- Giải sgk Toán 11 - KNTT
- Giải sgk Vật Lí 11 - KNTT
- Giải sgk Hóa học 11 - KNTT
- Giải sgk Sinh học 11 - KNTT
- Giải sgk Lịch Sử 11 - KNTT
- Giải sgk Địa Lí 11 - KNTT
- Giải sgk Giáo dục KTPL 11 - KNTT
- Giải sgk Tin học 11 - KNTT
- Giải sgk Công nghệ 11 - KNTT
- Giải sgk Hoạt động trải nghiệm 11 - KNTT
- Giải sgk Giáo dục quốc phòng 11 - KNTT
- Giải sgk Âm nhạc 11 - KNTT
- Lớp 11 - Chân trời sáng tạo
- Soạn văn 11 (hay nhất) - CTST
- Soạn văn 11 (ngắn nhất) - CTST
- Giải sgk Toán 11 - CTST
- Giải sgk Vật Lí 11 - CTST
- Giải sgk Hóa học 11 - CTST
- Giải sgk Sinh học 11 - CTST
- Giải sgk Lịch Sử 11 - CTST
- Giải sgk Địa Lí 11 - CTST
- Giải sgk Giáo dục KTPL 11 - CTST
- Giải sgk Hoạt động trải nghiệm 11 - CTST
- Giải sgk Âm nhạc 11 - CTST
- Lớp 11 - Cánh diều
- Soạn văn 11 Cánh diều (hay nhất)
- Soạn văn 11 Cánh diều (ngắn nhất)
- Giải sgk Toán 11 - Cánh diều
- Giải sgk Vật Lí 11 - Cánh diều
- Giải sgk Hóa học 11 - Cánh diều
- Giải sgk Sinh học 11 - Cánh diều
- Giải sgk Lịch Sử 11 - Cánh diều
- Giải sgk Địa Lí 11 - Cánh diều
- Giải sgk Giáo dục KTPL 11 - Cánh diều
- Giải sgk Tin học 11 - Cánh diều
- Giải sgk Công nghệ 11 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 11 - Cánh diều
- Giải sgk Giáo dục quốc phòng 11 - Cánh diều
- Giải sgk Âm nhạc 11 - Cánh diều

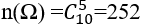
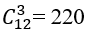



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

