Bài toán thực tế về căn bậc hai và căn thức bậc hai lớp 9 (cách giải + bài tập)

Chuyên đề phương pháp giải bài tập Một số bài toán thực tế liên quan đến căn bậc hai và căn thức bậc hai lớp 9 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Một số bài toán thực tế liên quan đến căn bậc hai và căn thức bậc hai.

Bài toán thực tế về căn bậc hai và căn thức bậc hai lớp 9 (cách giải + bài tập)

1. Cách giải bài tập

Để giải bài toán thực tế liên quan đến căn bậc hai và căn thức bậc hai, ta làm như sau:

Bước 1: Gọi đại lượng cần tìm là a, x, b,.....

Bước 2: Tìm điều kiện xác định của biểu thức chứa ẩn.

Bước 3: Giải phương trình, căn thức, biểu thức,.. vừa xây đựng được từ đề bài.

Bước 4: Kiểm tra điều kiện với giá tị vừa tìm được và kết luận.

2. Ví dụ minh họa

Ví dụ 1. Trong một thí nghiệm, một vật rơi tự do từ độ cao 80 m so với mặt đất. Biết rằng quãng đường dịch chuyển được của vật đó tính theo đơn vị mét được cho bởi công thức h = 5t² với t là thời gian vật đó rơi, tính theo đơn vị giây

(t > 0). Hỏi sau bao nhiêu lâu kể từ lúc rơi thì vật đó chạm đất?

Hướng dẫn giải

Khi vật chạm đất thì quãng đường dịch chuyển được của vật đó là 80 m.

Ta có: 80 = 5t² hay t² = 16.

Do đó, t = $\sqrt{16}$ = 4 hoặc t = $-\sqrt{16}$ = −4.

Mà t > 0 nên t = 4.

Vậy sau 4 giây kể từ lúc tơi thì vật đó chạm đất.

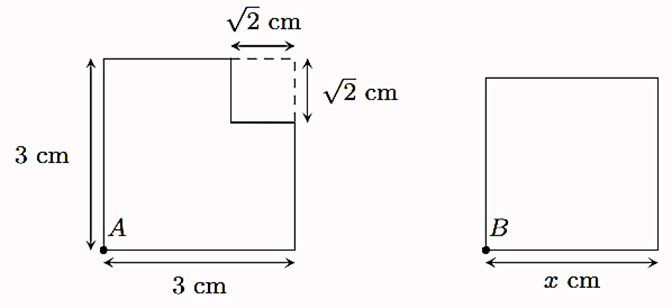
Ví dụ 2. Biết rằng hình A và hình B có diện tích bằng nhau. Tính độ dài cạnh x của hình vuông B.

Hướng dẫn giải

Diện tích hình A là: 3² – ${\left(\sqrt{2}\right)}^2$ = 9 – 2 = 7 (cm²).

Theo đề, ta có diện tích hình B cùng là 7 cm².

Suy ra x = $\sqrt{7}$ cm.

3. Bài tập tự luyện

Bài 1. Trong vật lí, quãng đường S (tính bằng mét) của một vật rơi tự do được cho bởi công thức S = 4,9t², trong đó l là tời gian rơi (tính bằng giây). Hỏi sau bao nhiêu giây thì vật sẽ chạm đất nếu được thả rơi tự do từ độ cao 122,5 mét?

A. 5s.

B. 15s.

C. 25s.

D. 20s.

Hướng dẫn giải

Đáp án đúng là: A

Từ công thức S = 4,9t² suy ra t² = $\frac{S}{4,9}$, suy ra t = $\sqrt{\frac{S}{4,9}}$ (vì t > 0).

Vật đang ở độ cao 122,5 m rơi chạm đất thì vật đã rơi được quãng đường là

S = 122,5 m.

Thay S = 122,5 m vào phương trình t = $\sqrt{\frac{S}{4,9}}=\sqrt{\frac{122,5}{4,9}}=5\left(s\right)$.

Vậy sau 5 s thì vật rơi chạm đất.

Bài 2. Để lái xe an toàn khi đi qua đoạn đường có dạng cung tròn, người lái cần biết tốc độ tối đa cho phép là bao nhiêu. Vì thế, ở những đoạn đường đó thường có bảng chỉ dẫn cho tốc độ tối đa cho phép của ô tô. Tốc độ tối đa cho phép v (m/s) được tính bởi công thức v = $\sqrt{rgu}$, trong đó r(m) là bán kính của cung đường g = 9,8 m/s², μ = 0,12 là hệ số ma sát trượt của đường. Tính vận tốc tối đa cho phép v (m/s) để lái xe an toàn khi đi qua đoạn đường có dạng cung tròn với bán kính r = 400 m (làm tròn đến hàng phần mười).

A. 22 m/s.

B. 20 m/s.

C. 2,2 m/s.

D. 0,22 m/s.

Hướng dẫn giải

Đáp án đúng là: A

Ta có công thức: v = $\sqrt{rgu}$.

Thay r = 400, g = 9,8 và μ = 0,12, ta có:

v = $\sqrt{400.9,8.0,12}$ ≈ 22 m/s.

Vậy tốc độ tối đa cho phép là khoảng 22 m/s.

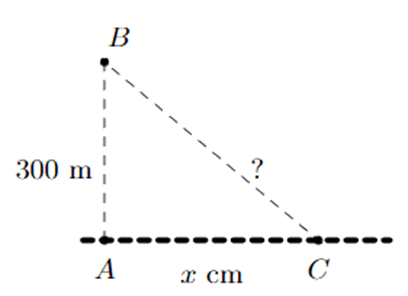
Bài 3. Một trạm phát sóng được đặt ở vị trí B cách đường tàu một khoảng

AB = 300 (m). Đầu tàu đang ở vị trí C, cách vị trí A một khoảng AC = x (m). Tính khoảng cách BC khi AC = 1 000 mét.

A. 1 404 m.

B. 1 044 m.

C. 1 400 m.

D. 1 440 m.

Hướng dẫn giải

Đáp án đúng là: B

Ta có khoảng cách từ trạm sóng đên đầu tàu là

BC $=\sqrt{A{B}^2+A{C}^2}=\sqrt{{300}^2+{1000}^2}\approx 1044$ (m).

Bài 4. Để chuẩn bị trồng cây trên vỉa hè, người ta để lại những ô đất hình tròn có diện tích khoảng 2 cm². Em hãy ước lượng (với độ chính xác 0,005) đường kính của các ô đất đó khoảng bao nhiêu mét?

A. 0,8 m.

B. 1,6 m.

C. 16 m.

D. 8 m.

Hướng dẫn giải

Đáp án đúng là: B

Ta có diện tích ô đất hình tròn là S = πr², suy ra r = $\sqrt{\frac{S}{\pi }}=\sqrt{\frac{2}{\pi }}$ (m).

Đường kính của các ô đất đó là: d = 2r ≈ 1,6 m.

Bài 5. Đại Kim tự táp Giza là Kim tự tháp Ai Cập lớn nhất và là lăng mộ của Vương triều thứ Tư của pharaoh Khufu. Nền kim tự tháp có dạng hình vuông với diện tích khoảng 53 052 m². Hỏi độ dài cạnh nền của kim tự tháp đó là bao nhiêu mét? (làm tròn kết quả đến hàng phần mười)

A. 23,03 m.

B. 23,3 m.

C.230,3 m.

D. 203 m.

Hướng dẫn giải

Đáp án đúng là: C

Gọi cạnh hình vuông (nền kim tự tháp) là x, điều kiện x > 0, đơn vị m.

Diện tích hình vuông là: x² = 53 052.

Suy ra x = $\sqrt{53052}$ ≈ 230,3 m.

Vậy độ dài cạnh nền của kim tự tháp khoảng 230,3 m.

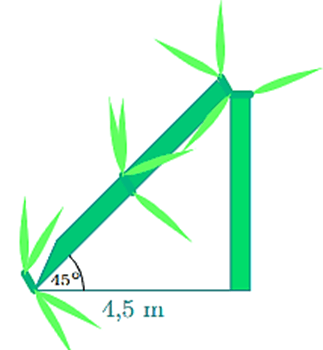
Bài 6. Giông bão thổi mạnh, một cây bị gãy gập xuống làm ngọn cây chạm đất và tạo với phương nằm ngang một góc 45° (minh họa ở hình bên). Người ta đo được khoảng cách từ chỗ ngọn cây đến gốc cây là 4,5 m. Giả sử cây mọc vuông góc với mặt đấy, hãy tính chiều cao của cây đó theo đơn vị mét (làm tròn kết quả đến hàng phần mười).

A. 4,5 m.

B. 10,9 m.

C.19 m.

D. 9 m.

Hướng dẫn giải

Đáp án đúng là: B

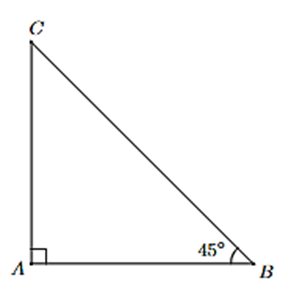
Xem đoạn bị gãy là CB, đoạn còn lại (thẳng đứng) là AC.

Như vậy, độ dài của cây khi chưa bị gãy là AC + BC.

Do tam giác ABC vuông tại A và $\widehat{ABC}$ = 45°, suy ra tam giác ABC vuông cân tại A.

Suy ra AC = AB = 4,5 m.

Áp dụng định lí Pythagore trong tam giác ABC, ta có:

AB² + AC² = BC²

4,5² + 4,5² = BC²

Suy ra BC = $\sqrt{2.4,5^2}=\sqrt{40,5}$ m.

Vậy chiều cao cây trước khi gãy là: 4,5 + $\sqrt{40,5}$ ≈ 10,9 m.

Sử dụng dữ kiện bài toán dưới đây để trả lời Bài 7, 8.

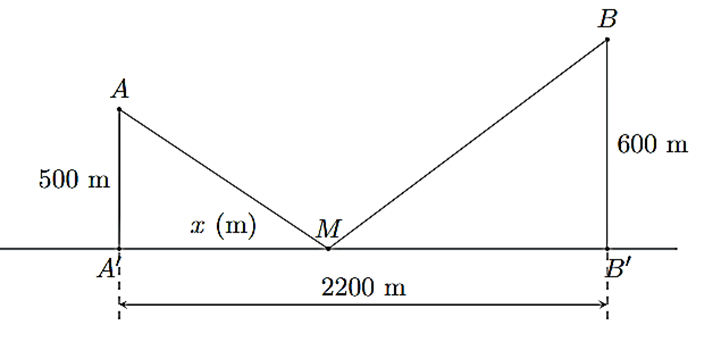
Có hai xã A, B cùng ở bên bờ sông Lam, khoảng cách từ hai xã đó đến bờ sông lần lượt là AA' = 500 m, BB' = 600 m và người ta đo được A'B' = 2 200 m. Các kĩ sư muốn xây một trạm cung cấp nước sạch đó là điểm M trên đoạn

MA' = x (m), 0 < x < 2 200 (minh họa ở hình bên).

Bài 7. Tổng khoảng cách MA + MB theo x là:

A.$\sqrt{{500}^2+x^2}$ + $\sqrt{{600}^2+{\left(2200-x\right)}^2}$.

B.$\sqrt{{500}^2+x^2}$ −$\sqrt{{600}^2+{\left(2200-x\right)}^2}$.

C.$\sqrt{{600}^2+{\left(2200-x\right)}^2}$ − $\sqrt{{500}^2+x^2}$.

D. −$\sqrt{{500}^2+x^2}$ − $\sqrt{{600}^2+{\left(2200-x\right)}^2}$.

Hướng dẫn giải

Đáp án đúng là: A

Xét ∆AA'M vuông tại A' có MA = $\sqrt{A{A^{\text{'}}}^2+A^{\text{'}}{M}^2}=\sqrt{{500}^2+x^2}$ (m).

Xét ∆BB'M vuông tại B' có MB = $\sqrt{B{B^{\text{'}}}^2+B^{\text{'}}{M}^2}=\sqrt{{600}^2+{\left(2200-x\right)}^2}$ (m).

Khi đó MA + MB = $\sqrt{{500}^2+x^2}$ + $\sqrt{{600}^2+{\left(2200-x\right)}^2}$ (m).

Bài 8. Tổng khoảng cách MA + MB khi x = 1200 là (làm tròn kết quả đến hàng đơn vị của mét)

A. 2 466 m.

B. 2 664 m.

C. 2 400 m.

D.2 600 m.

Hướng dẫn giải

Đáp án đúng là: A

Với x = 1 200, ta có:

MA + MB = $\sqrt{{500}^2+{1200}^2}$ + $\sqrt{{600}^2+{\left(2200-1200\right)}^2}$ ≈ 2 466 (m).

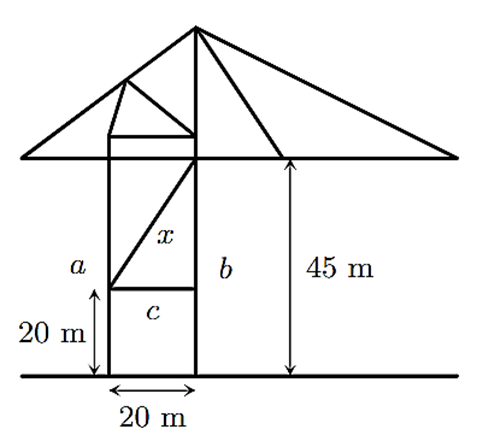
Bài 9. Trên cần trục ở Hình 5, hai trụ a và b đứng cách nhau 20 m, hai xà ngang c và d lần lượt có độ cao 20 m và 45 m so với mặt đất. Xà chéo x có độ dài bao nhiêu mét? (Kết quả làm tròn đến hàng đơn vị)

A. 20 m.

B. 32 m.

C. 16 m.

D. 15 m.

Hướng dẫn giải

Đáp án đúng là: B

Theo định lý Pythagore, ta có: x = $\sqrt{c^2+b^2}$.

Theo đề, ta có: b = 45 – 20 = 25 và c = 20.

Suy ra x = $\sqrt{{25}^2+{20}^2}=\sqrt{1025}$ ≈ 32.

Vậy xà chéo x có độ dài khoảng 32 m.

Bài 10. Hệ quả của hiện tượng nóng lên toàn cầu là băng của một số sông băng đang tan chảy. Mười hai năm sau khi băng biến mất, những loài thực vật nhỏ bé, được gọi là địa y, bắt đầu mọc trên đá. Mỗi nhóm địa y phát triển ở dạng (gần như) một hình tròn. Đường kính d (mm) của hình tròn này và tuổi của địa y có thể được tính gần đúng bằng công thức $d=7\sqrt{t-12}$ với t là số năm tính từ khi băng biến mất (t ≥ 12). Tính đường kính của hình tròn địa y tạo nên sau khi băn biến mất 16 năm.

A. 7 mm.

B. 14 mm.

C. 8 mm.

D.16 mm.

Hướng dẫn giải

Đáp án đúng là: B

Đường kính của hình tròn do địa y tạo nên sau khi băng biến mất 16 năm là:

7$\sqrt{16-12}$ = 7.2 = 14 (mm).

Xem thêm các dạng bài tập Toán 9 hay, chi tiết khác:

• Khai căn bậc hai của phép nhân
• Khai căn bậc hai của phép chia
• So sánh các căn bậc hai
• Một số bài toán thực tế liên quan đến khai căn bậc hai
• Đưa thừa số ra ngoài hoặc vào trong dấu căn thức bậc hai

• Hơn 20.000 câu trắc nghiệm Toán,Văn, Anh lớp 9 có đáp án

---