Bài toán thực tế về tỉ số lượng giác của góc nhọn lớp 9 (cách giải + bài tập)

Chuyên đề phương pháp giải bài tập Một số bài toán thực tế liên quan đến tỉ số lượng giác của góc nhọn lớp 9 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Một số bài toán thực tế liên quan đến tỉ số lượng giác của góc nhọn.

Bài toán thực tế về tỉ số lượng giác của góc nhọn lớp 9 (cách giải + bài tập)

1. Cách giải bài tập

• Sử dụng các tỉ số lượng giác của góc nhọn để thực hiện giải các bài toán thực tế liên quan.

2. Ví dụ minh họa

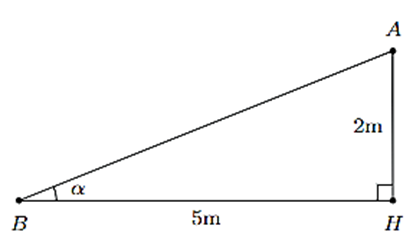
Ví dụ 1. Hình bên mô tả tia nắng mặt trời dọc theo AB tạo với phương nằm ngang trên mặt đất một góc α = $\widehat{ABH}$. Biết AH = 2 m, BH = 5 m. Tính số đo góc α (làm tròn kết quả đến hàng đơn vị của độ).

Hướng dẫn giải

Xét tam giác vuông ABH, ta có tanα = $\frac{AH}{BH}=\frac{2}{5}$.

Sử dụng máy tính cầm tay, ta tính được α ≈ 21,8°.

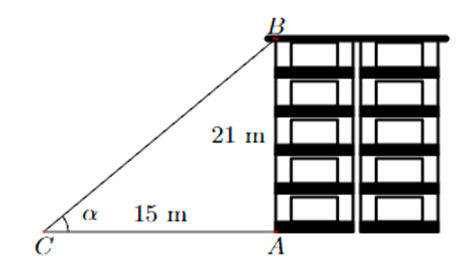
Ví dụ 2. Tia nắng chiều qua nóc của một tòa nhà hợp với mặt đất một góc α. Cho biết tòa nhà cao 21 m và bóng của nó trên mặt đất dài 15 m. Tính góc α. (Kết quả làm tròn đến độ)

Hướng dẫn giải

Xét tam giác ABC vuông tại A:

Ta có: tanα = $\frac{AB}{AC}=\frac{21}{15}$, sử dụng máy tính cầm tay ta tính được α ≈ 54°.

3. Bài tập tự luyện

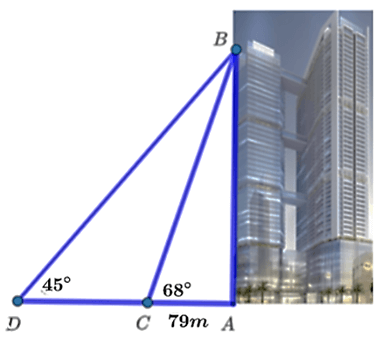
Bài 1. Tháp Discovery Complex A với quy mô 54 tầng, đang là tòa nhà cao nhất quận Cầu Giấy. Tại một thời điểm trong ngày mặt trời tạo với mặt đất một góc xấp xỉ 68° và bóng của tòa nhà trên mặt đất dài khoảng 79 m. Hỏi tòa nhà cao bao nhiêu mét? (Làm tròn kết quả đến hàng đơn vị).

A. 196 m.

B. 277 m.

C. 169 m.

D. 275 m.

Hướng dẫn giải

Đáp án đúng là: A

Chiều cao của tòa tháp chính là độ dài của đoạn AB.

Xét tam giác ABC vuông tại A, ta có: AB = AC. $\tan \widehat{ACB}$ = 79.tan68° ≈ 196 m.

Sử dụng dữ kiện bài toán sau để trả lời Bài 2, 3.

Tháp chung cư cư Discovery Complex A với quy mô 54 tầng, đang là tòa nhà cao nhất quận Cầu Giấy. Tại một thời điểm trong ngày, tia nắng mặt trời tạo với mặt đất một góc xấp xỉ 67° và bóng của tòa nhà trên mặt đất dài khoảng 72 m.

Bài 2. Tính chiều cao của tòa tháp chung cư (làm tròn đến kết quả hàng đơn vị)

A. 240 m.

B. 170 m.

C. 107 m.

D. 172 m.

Hướng dẫn giải

Đáp án đúng là: B

Chiều cao của tòa tháp chính là độ dài đoạn AB.

Xét tam giác ABC vuông tại A, ta có:

AB = AC.tan$\widehat{ACB}$ = 72.tan67° ≈ 170 m.

Bài 3. Một flycam từ vị trí D bay lên đỉnh B theo quãng đường BD, tạo với phương nằm ngang một góc bằng 45°. Biết flycam mất 140 giây để lên đến đỉnh tháp. Tính vận tốc trung bình của chiếc flycam đó (làm tròn kết quả đến hàng phần trăm).

A. 1,7 m/s.

B. 1,72 m/s.

C. 1,27 m/s.

D. 17,2 m/s.

Hướng dẫn giải

Đáp án đúng là: B

Xét tam giác vuông ABD có: BD = $\frac{AB}{\sin \widehat{ADB}}=\frac{170}{\sin 45°}=170\sqrt{2}$ (m).

Vận tốc trung bình của chiếc flycam đó là: $170\sqrt{2}:140\approx 1,72\left(m/s\right)$.

Vậy vận tốc trung bình của chiếc flycam đó khoảng 1,72 m/s.

Sử dụng dữ kiện bài toán sau để trả lời cho Bài 4,5.

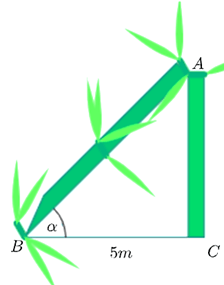
Sau một trận bão lớn, một cái cây mọc thẳng đứng ở cị trí C đã gãy ngang tại A (như hình vẽ). Ngọn cây chạm mặt đất cách gốc một khoảng BC = 5 m. Biết rằng phần ngọn bị gãy AB và phần gốc AC có tỉ lệ 3:2.

Bài 4. Tính góc α tạo bởi phần thân bị gãy AB và mặt đất BC (kết quả làm tròn đến phút).

A. $43°{15}^{\text{'}}$.

B. $41°{49}^{\text{'}}$.

C. $42°{49}^{\text{'}}$

D. $45°{49}^{\text{'}}$.

Hướng dẫn giải

Đáp án đúng là: B

Theo đề bài, ta có, phần ngọn bị gãy AB và phần gốc AC có tỉ lệ 3 : 2 hay $\frac{AB}{AC}=\frac{3}{2}$, suy ra $\frac{AC}{AB}=\frac{2}{3}$.

Xét tam giác ABC vuông tại C, ta có: $\sin \widehat{ABC}=\frac{AC}{AB}=\frac{2}{3}$,

suy ra $\alpha =\tan \widehat{ABC}=41°{49}^{\text{'}}$.

Vậy góc α tạo bởi phần thân bị gãy AB và mặt đất BC khoảng α ≈ 41°49’.

Bài 5. Hỏi chiều cao ban đầu của cây là bao nhiêu mét? (kết quả làm tròn đến chữ số thập phân thứ hai).

A. 6,71 m.

B. 11,2 m.

C. 11,18 m.

D. 11,175 m.

Hướng dẫn giải

Đáp án đúng là: C

Xét tam giác ABC vuông tại C, ta có: AC = BC.tan$\widehat{ABC}$ = 5.tan41°49’ ≈ 4,47 (m).

Mà $\frac{AB}{AC}=\frac{3}{2}$, suy ra AB = $\frac{3}{2}$AC ≈ $\frac{3}{2}$.4,47 = 6,705 (m).

Độ dài cây ban đầu là tổng của phần ngọn bị gãy AB và phần gốc AC.

Vậy chiều cao ban đầu của cây khoảng: 4,47 + 6,705 = 11,175 ≈ 11,18 (m).

Bài 6. Hai người A và B đứng cùng bờ sông nhìn ra một cồn nổi giữa sông. Người A nhìn ra cồn với một góc 43° so với bờ sông, người B nhìn ra cồn với một góc 28° so với bờ sông. Hai người đứng cách bờ sông 250 m. Hỏi cồn cách bờ sông hai người đứng bao nhiêu mét? (Kết quả làm tròn đến hàng phần trăm)

A. 85 m.

B. 86, 44 m.

C. 84,66 m.

D. 84 m.

Hướng dẫn giải

Đáp án đúng là: C

Khoảng cách của cồn và bờ sông hai người đứng chính là độ dài đoạn thẳng CH.

Xét tam giác AHC vuông tại H, ta có:

$\tan \widehat{CAH}=\frac{CH}{AH}$> nên $AH=\frac{CH}{\tan \widehat{CAH}}=\frac{CH}{\tan 43°}$. (1)

Xét tam giác BHC vuông tại H, ta có:

$\tan \widehat{CBH}=\frac{CH}{BH}$ nên $BH=\frac{CH}{\tan \widehat{CBH}}=\frac{CH}{\tan 28°}$. (2)

Từ (1) và (2) ta có:

AB + AH + BH = $\frac{CH}{\tan 43°}+\frac{CH}{\tan 28°}=CH\left(\frac{1}{\tan 43°}+\frac{1}{\tan 28°}\right)$

Do đó, $CH=\frac{AB}{\frac{1}{\tan 43°}+\frac{1}{\tan 28°}}=\frac{250}{\frac{1}{\tan 43°}+\frac{1}{\tan 28°}}\approx 84,66\text{(m).}$

Vậy cồn cách bờ sông hai người đứng khoảng 84,66 m.

Bài 7. Trong lần đến thăm quan tháp Eifel (ở thủ đô Paris, Pháp), bạn Vân muốn ước tính độ cao của tháp. Sau khi quan sát, bạn Vân đã minh họa lại kết quả đo đạc ở hình bên. Em hãy giúp bạn Vân tính độ cao h của tháp theo đơn vị mét (làm tròn kết quả đến hàng đơn vị).

A. 326 m.

B. 362 m.

C. 236 m.

D. 263 m.

Hướng dẫn giải

Đáp án đúng là: A

Xét tam giác ADC vuông tại C, ta có: AC = h.cot$\widehat{DAC}$ = h.cot60° (m)

Xét tam giác BDC vuông tại C, ta có: BC = h.cot$\widehat{DBC}$ = h.cot75° (m).

Do AC – BC = AB = 101 nên h.cot60° − h.cot75° = 101

Suy ra h = $\frac{101}{\cot 60°-\cot 75°}\approx 326$ (m).

Vậy tháp Eiffel có độ cao khoảng 326 (m).

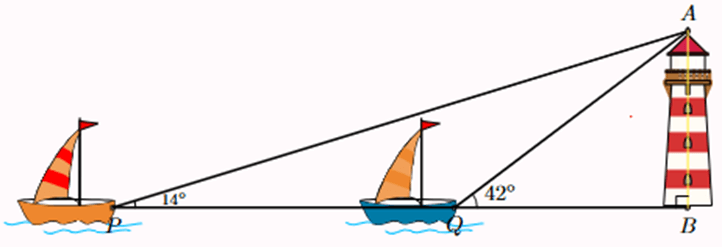
Sử dụng dữ kiện của bài toán dưới đây để trả lời cho Bài 8, 9 , 10.

Hai con thuyền P và Q cách nhau 300 m và thẳng hàng với chân B của tháp hải đăng ở trên bờ biển. Từ P và Q, người ta nhìn thấy tháp hải đăng dưới các góc $\widehat{BPQ}=14°$ và $\widehat{BQA}=42°$. Đặt h = AB là chiều cao của tháp hải đăng.

Bài 8. Độ dài BQ theo h là

A. $\frac{h}{\tan 42°}$.

B. $\frac{h}{\cot 42°}$.

C. $\frac{h}{\tan 14°}$.

D. $\frac{h}{\cot 14°}$.

Hướng dẫn giải

Đáp án đúng là: A

Xét tam giác BQA vuông tại B, ta có:

tanQ = $\frac{AB}{QB}$ nên BQ = $\frac{AB}{QB}$ nên BQ = $\frac{AB}{\tan 42°}=\frac{h}{\tan 42°}$.

Bài 9. Độ dài BP theo h là

A. $\frac{h}{\tan 42°}$.

B. $\frac{h}{\cot 42°}$.

C. $\frac{h}{\tan 14°}$.

D. $\frac{h}{\cot 14°}$.

Hướng dẫn giải

Đáp án đúng là: C

Xét tam giác BPA vuông tại B, ta có:

tanP = $\frac{AB}{PB}$ nên $PB=\frac{AB}{\tan 14°}=\frac{h}{\tan 14°}$.

Bài 10. Chiều cao cuủa tháp hải đăng (làm tròn đến hàng phần mười) là:

A. 103 m.

B. 103,4 m.

C. 104 m.

D. 104,3 m.

Hướng dẫn giải

Đáp án đúng là: B

Ta có: BP – BQ = 300.

Suy ra $\frac{h}{\tan 42°}-\frac{h}{\tan 14°}=300$.

Suy ra h = $\frac{300}{\frac{1}{\tan 14°}-\frac{1}{\tan 42°}}\approx 103,4$ (m).

Vậy chiều cao của tháp hải đăng là khoảng 103,4 m.

Xem thêm các dạng bài tập Toán 9 hay, chi tiết khác:

• Tính tỉ số lượng giác trong tam giác vuông
• Chứng minh đẳng thức liên quan đến tỉ số lượng giác
• Giải tam giác vuông
• Tính cạnh, góc và diện tích tam giác
• Ứng dụng tỉ số lượng giác của góc nhọn để ước lượng khoảng cách, chiều cao

• Hơn 20.000 câu trắc nghiệm Toán,Văn, Anh lớp 9 có đáp án

---