Bài toán thực tế lớp 9 Nón; Trụ; Cầu và hình khối

Bài toán thực tế lớp 9 Nón; Trụ; Cầu và hình khối có lời giải chương trình mới dùng chung cho ba sách Kết nối tri thức, Chân trời sáng tạo, Cánh diều với bài tập đa dạng giúp Giáo viên có thêm tài liệu giảng dạy các dạng toán thực tế lớp 9.

Bài toán thực tế lớp 9 Nón; Trụ; Cầu và hình khối

Xem thử

Chỉ từ 200k mua trọn bộ Chuyên đề, các dạng Toán thực tế lớp 9 chương trình mới bản word trình bày đẹp mắt, chỉnh sửa dễ dàng:

• B1: gửi phí vào tk: 1053587071 - NGUYEN VAN DOAN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận đề thi

1. CÔNG THỨC

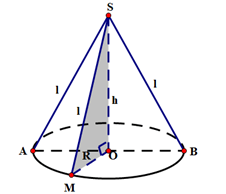
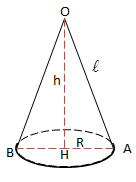
Hình nón

Đường cao: h = SO. (SO cũng được gọi là trục của hình nón).

Bán kính đáy: $R=OA=OB=OM.$

Đường sinh: $l=\text{SA}=\text{SB}=\text{SM.}$

Thể tích: $\text{V}=\frac{1}{3}\text{h}\cdot {\text{S}}_{\text{d}}=\frac{1}{3}\text{h}\cdot \pi {\text{R}}^2$. (liên tuởng đến thể tich khối chóp).

Diện tích xung quanh: ${\text{S}}_{\text{xq}}=\pi \text{r}l.$

Diện tích toàn phần: ${\text{S}}_{\text{tp}}={\text{S}}_{\text{xq}}+{\text{S}}_{\text{d}}=\pi \text{r}l+\pi {\text{r}}^2\text{.}$

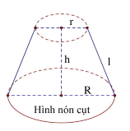
Hình nón cụt

Diện tích xung quanh: $S_{xq}=\pi \left(R+r\right)l$

Diện tích toàn phần:

$S_{tp}=S_{xq}+S_{2day}=\pi [R^2+r^2+\left(R+r\right)l]$

Thể tích: $V=\frac{\pi h}{3}\left(R^2+r^2+rR\right)$

2. BÀI TẬP VẬN DỤNG

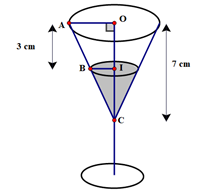
Câu 1: Một cái ly thủy tinh (như hình vẽ), phần phía trên là hình nón có chiều cao 7 cm, có đáy đường tròn bán kính 4 cm. Biết thể tích hình nón được tính theo công thức $\text{V}=\frac{1}{3}\pi {\text{r}}^2\text{h}$ với r là bán kính đường tròn đáy của hình nón; h là chiều cao của hình nón.

a) Tính thể tích của cái ly (bề dày của ly không đáng kể).

b) Biết trong ly đang chứa rượu với mức rượu đang cách miệng ly là 3 cm. Hỏi thể tích còn lại của ly rượu chiếm bao nhiêu phần của thể tích ly. (kết quả làm tròn đến chữ số thập phân thứ hai; lấy $\pi \approx 3,14$.)

Lời giải

a) Thể tích của cái ly: ${\text{V}}_1=\frac{1}{3}\pi {\text{OA}}^2\cdot \text{OC}=\frac{1}{3}\pi \cdot 4^2\cdot 7$$=\frac{112}{3}\pi \approx 117,23\left({\text{cm}}^3\right)$

b) Ta có: $\text{IB//OA}\Rightarrow \frac{\text{CI}}{\text{CO}}=\frac{\text{IB}}{\text{OA}}$ (hệ quả của định lí Thales) $\Rightarrow \text{IB}=\frac{\text{CI}\cdot \text{OA}}{\text{CO}}=\frac{(7-3)\cdot 4}{7}=\frac{16}{7}$

Thể tích rượu có trong ly: ${\text{V}}_2=\frac{1}{3}\pi {\text{IB}}^2\cdot \text{CI}$$=\frac{1}{3}\pi \cdot {\left(\frac{16}{7}\right)}^2\cdot 4=\frac{1024}{147}\pi \left({\text{cm}}^3\right)$

Thể tích còn lại trong ly (phần không chứa rượu): ${\text{V}}_3={\text{V}}_1-{\text{V}}_2=$$\frac{112}{3}\pi -\frac{1024}{147}\pi =\frac{1488}{49}\pi$

Vậy thể tích còn lại của ly rượu chiếm $\frac{{\text{V}}_3}{{\text{V}}_1}\cdot 100\%\approx 81,34\%$ thể tích ly.

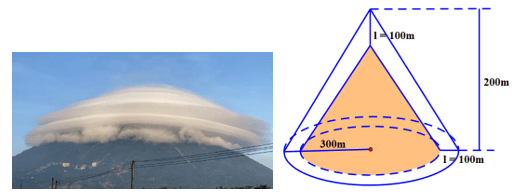
Câu 2: Vừa qua trên mạng xã hội, nhiều người dùng truyền tai nhau hình ảnh về một hiện tượng tự nhiên vô cùng kỳ lạ, xuất hiện vào sáng ngày 24/11/2022. Được biết, bức ảnh này được chụp lại núi Bà Đen, một địa điểm du lịch vô cùng nổi tiếng của Tây Ninh.

Trong hình ảnh, đỉnh núi được bao phủ bởi một lớp mây trắng xóa. Không chỉ có vậy, những đám mây còn tạo thành một lớp “vỏ” có phần kỳ bí. Nhiều người gọi đây là hiện tượng “mây vờn”, có người nhận xét trông đám mây như một chiếc nón. Ước tính chiều cao của nón là 200 m, bán kính đáy của nón là 300 m, độ dày đám mây là $l=100m$. Tính thể tích đám mây?

Biết thể tích hình nón là $V=\frac{1}{3}\pi R^{2}h$ (trong đó R là bán kính đường tròn đáy; h là chiều cao hình nón, lấy $\pi \approx 3,14$, các kết quả làm tròn chữ số thập phân thứ nhất).

Lời giải

Thể tích hình nón lớn: ${\text{V}}_{\text{lon}}=\frac{1}{3}\pi {\text{R}}^2\text{h}=\frac{1}{3}\pi {\text{R}}^2\text{h}$$=\frac{1}{3}\cdot 3,14\cdot {300}^2\cdot 200=18840000\left({\text{m}}^3\right)$

Thể tích hình nón nhỏ:

${\text{V}}_{\text{nho}}=\frac{1}{3}\pi {\text{R}}^2\text{h}=\frac{1}{3}\pi {\text{R}}^2\text{h}$$=\frac{1}{3}\cdot 3,14\cdot {(300-100)}^2\cdot (200-100)$$=\frac{12560000}{3}\left({\text{m}}^3\right)$

Thể tích đám mây là: ${\text{V}}_{\text{mây}}=18840000-\frac{12560000}{3}$$=\frac{43960000}{3}\approx 14653333,3\left({\text{m}}^3\right)$

Câu 3: Nón lá Câu thơ là một đặc trưng của xứ Huế. Nón thường được đan bằng các loại lá khác nhau như lá cọ, lá buông, rợ, tre, lá cối, lá hồ, lá du quy diệp chuyên làm nón,. Để làm ra một chiếc nón lá người thợ thủ công lấy từng chiếc lá, làm cho phẳng rồi lấy kéo cắt chéo đầu trên, rối lấy kim xâu chúng lại với nhau một lượt, sau đó xếp đều trên khuôn nón. Lá nón mỏng và cũng dễ hư khi gặp trời mưa nhiều nên các thợ thủ công đã tận dụng bẹ tre khô để làm lớp giữa hai lớp lá nón làm cho nón vừa cứng lại vừa bền. Đường kính của vòng tròn lớn nhất của chiếc nón khoảng 40 cm; chiều cao của chiếc nón là khoảng 19 cm. Hỏi cần bao nhiêu chiếc lá đã làm phẳng đề làm thành 1 chiếc nón lá, biết rằng diện tích 1 chiếc lá làm phẳng là $72c{m}^2$, diện tích xung quanh của hình nón là $S_{xq}=\pi rl$ ($\pi =3,14$; làm tròn đến hàng đơn vị)

Lời giải

Diện tích xung quanh của hình nón là: ${\text{S}}_{\text{xq}}=\pi \text{rl}=3,14\cdot \frac{40}{2}\cdot 19\approx 1193{\text{cm}}^2$

Số lượng chiếc lá phẳng cần là: $1193:72\approx 17$ (chiếc)

Câu 4: Một hình nón có bán kính đáy bằng 5 cm và diện tích xung quanh là $65\pi c{m}^2$. Tính thể tích của hình nón đó.

Lời giải

Diện tích xung quang của hình nón là: $S_{xq}=\pi Rl=\pi 5l$

Theo đề Câu, ta có $S_{xq}=65\pi \Rightarrow 65\pi =\pi \mathrm{.5.}l$$\iff l=13cm$

Gọi H là tâm của đường tròn đáy, AB là đường kính của (H), O là đỉnh của hình nón.

Xét $\Delta OHA$ vuông tại H, có:

$O{A}^2=O{H}^2+A{H}^2\Rightarrow O{H}^2$$=O{A}^2-A{H}^2={13}^2-5^2$$=169-25=144\Rightarrow OH=12cm$

Thể tích của hình nón là: $V=\frac{1}{3}\pi R^{2}h=\frac{1}{3}\pi {.5}^2.12$$=100\pi \left(c{m}^3\right)$

Câu 5: Nón Huế là một hình nón có đường kính đáy bằng 40 cm, độ dài đường sinh là 30 cm. Người ta lát mặt xung quanh hình nón bằng ba lớp lá khô. Tính diện tích lá cần dùng đề tạo nên một chiếc nón Huế như vậy (làm tròn $c{m}^2$)

Lời giải

Chiếc nón Huế là một hình nón có đường kính đáy d = 40 (cm), nên bán kính đáy $R=\frac{d}{2}=\frac{40}{2}=20\left(cm\right)$

Độ dài đường sinh: $l=30\left(cm\right)$

Vậy diện tích xung quanh của hình nón này là: $S=\pi Rl=3,\mathrm{14.20.30}=1884\left(c{m}^2\right)$

Vì người ta lợp nón bằng 3 lớp lá, nên diện tích lá cần dùng để tạo nên một chiếc nón Huế sẽ là: $1884.3=5652\left(c{m}^2\right)\text{.}$

................................

................................

................................

Xem thử

Xem thêm Chuyên đề Toán thực tế lớp 9 chương trình mới có lời giải hay khác:

• Bài toán thực tế lớp 9 Căn thức

• Bài toán thực tế lớp 9 Tỉ số lượng giác; Hệ thức lượng trong tam giác vuông

• Bài toán thực tế lớp 9 Hàm số bậc hai và giải bài toán bằng cách lập phương trình

• Bài toán thực tế lớp 9 Đường tròn; Đa giác nội tiếp; Đa giác đều

• Bài toán thực tế lớp 9 Một số yếu tố thống kê

• Bài toán thực tế lớp 9 Một số yếu tố xác suất

• Hơn 20.000 câu trắc nghiệm Toán,Văn, Anh lớp 9 có đáp án

---