(Ôn thi Toán vào 10) Giải và biện luận hệ phương trình bậc nhất hai ẩn và các bài toán liên quan
Giải và biện luận hệ phương trình bậc nhất hai ẩn và các bài toán liên quan nằm trong bộ Chuyên đề ôn thi Toán vào lớp 10 năm 2026 đầy đủ lý thuyết và bài tập đa dạng có lời giải chi tiết giúp học sinh có thêm tài liệu ôn thi vào lớp 10 môn Toán.
(Ôn thi Toán vào 10) Giải và biện luận hệ phương trình bậc nhất hai ẩn và các bài toán liên quan
Chỉ từ 500k mua trọn bộ 12 Chuyên đề ôn thi Toán vào lớp 10 năm 2026 theo cấu trúc mới bản word có lời giải chi tiết:
- B1: gửi phí vào tk:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án
I. KIẾN THỨC TRỌNG TÂM
1. Hệ phương trình bậc nhất hai ẩn
Hệ phương trình bậc nhất hai ẩn có dạng
Các số là các số thực cho trước và hai ẩn số là x và y. Khi các số không phải là các con số cụ thể, ta có hệ phương trình bậc nhất hai ẩn phụ thuộc tham số.
Khi đó ta có các điều kiện sau:
⦁ Hệ có nghiệm duy nhất khi
⦁ Hệ vô nghiệm khi
⦁ Hệ vô số nghiệm khi
2. Phương trình bậc nhất một ẩn
Phương trình có dạng
⦁ Nếu thì phương trình có vô số nghiệm.
⦁ Nếu thì phương trình vô nghiệm.
⦁ Nếu phương trình có nghiệm duy nhất
II. CÁC DẠNG TOÁN VÀ VÍ DỤ MINH HỌA
Dạng 1. Tìm giá trị tham số để hệ chứa tham số có nghiệm là
Ví dụ 1. Xác định tham số m để hệ phương trình nhận cặp số là nghiệm.
Hướng dẫn giải:
Để hệ phương trình nhận cặp số là nghiệm thì khi thay và vào hệ phương trình phải thỏa mãn, do đó:
Vậy không có giá trị của m để hệ nhận cặp số là nghiệm.
Ví dụ 2. Xác định tham số a; b để hệ phương trình nhận cặp số là nghiệm.
Hướng dẫn giải:
Để hệ phương trình nhận cặp số là nghiệm thì khi thay x = 1 và y = -2 vào hệ phương trình phải thỏa mãn, do đó: hay
Giải phương trình suy ra b = 3
Thế b = 3 vào phương trình (2), ta được: 2a + 3 = -5 suy ra 2a = -8 nên a = -4
Vậy và
Dạng 2. Biện luận số nghiệm của hệ phương trình
Ví dụ 3. Biện luận số nghiệm của hệ phương trình
Phân tích:
Xét hệ phương trình
Thưc hiện Bước 1. Rút x hoặc y ở một trong hai phương trình của hệ.
⦁ Nếu từ (2) rút x ta được nếu rút y ta được
Như vậy rút ẩn x hoặc ẩn y từ (2) ra cồng kềnh và phải biện luận trường hợp nếu rút y.
⦁Nếu từ (1) rút x ta được ta cũng phải biện luận trường hợp
Nếu rút y thì biểu thức này đơn giản hơn.
Hướng dẫn giải:
Xét hệ phương trình .
Từ phương trình (1) ta có
Thay vào phương trình (2) ta được:
Trường hợp 1. Xét hay hoặc
⦁ Với thì phương trình trở thành:
Suy ra phương trình này vô nghiệm.
Như vậy, với hệ phương trình đã cho vô nghiệm.
⦁Với thì phương trình trở thành:
Suy ra phương trình này vô nghiệm.
Như vậy, với hệ phương trình đã cho vô nghiệm.
Trường hợp 2. Xét hay và
Khi đó phương trình có nghiệm duy nhất
Thay vào ta có:
Kết luận: Nếu hoặc thì hệ phương trình vô nghiệm.
Nếu thì hệ phương trình có nghiệm duy nhất:
Dạng 3. Tìm tham số để hệ có nghiệm thỏa mãn tính chất, hoặc chứng minh tính chất nào đó của nghiệm
|
Phương pháp giải: Để giải được bài toán trên, ta thực hiện theo các bước: Bước 1.Tìm tham số để hệ có nghiệm. Bước 2. Tìm tham số để nghiệm thỏa mãn tính chất theo yêu cầu. Bước 3. Đối chiếu điều kiện hệ có nghiệm. Bước 4. Kết luận giá trị của tham số thỏa mãn đề bài. |
Ví dụ 4. Cho hệ phương trình . Tìm các giá trị của tham số a để hệ phương trình đã cho có nghiệm thỏa mãn điều kiện
Hướng dẫn giải:
Xét hệ phương trình:
Từ (1) ta có thay vào (2) ta được:
hay nên
Với mọi a ta có nên
Do đó phương trình (4) có nghiệm duy nhất với mọi giá trị của tham số a
Thay vào (3), ta được
Khi đó hệ phương trình có nghiệm duy nhất
Theo bài, tức là suy ra (do
Hay nên
Vậy để hệ phương trình có nghiệm thì .
Ví dụ 5. Tìm giá trị nguyên của tham số m để hệ phương trình có nghiệm duy nhất là nghiệm nguyên.
Hướng dẫn giải:
Xét hệ phương trình:
Từ (1) ta có thay vào (2) ta được:
Để hệ có nghiệm duy nhất thì phương trình phải có nghiệm duy nhất, tức là hay hay và
Khi đó phương trình (4) có nghiệm duy nhất:
Thay vào (3) ta được:
Vậy khi và thì hệ phương trình có nghiệm duy nhất
Ta có:
Để nghiệm nguyên thì và điều này xảy ra khi và chỉ khi
Suy ra Ư
Ta có bảng sau:
Kết hợp với điều kiện có nghiệm duy nhất của hệ là và ta được là các giá trị thỏa mãn yêu cầu đề bài.
Ví dụ 6. Cho hệ phương trình
Xác định giá trị của tham số m để hệ phương trình có nghiệm duy nhất thỏa mãn
Hướng dẫn giải:
Xét hệ phương trình
Nhân hai vế của phương trình (1) với 3, ta được hệ phương trình mới là
Trừ hai vế của phương trình và phương trình ta được:
suy ra
Thay vào phương trình (1), ta được:
suy ra hay
Do đó với mọi m thì hệ phương trình có nghiệm duy nhất là
Theo bài, nên hay
Trường hợp 1. nên suy ra
Trường hợp 2. nên suy ra
Vậy thỏa mãn yêu cầu đề bài.
Ví dụ 7. Cho hệ phương trình . Tìm tham số m để hệ phương trình có nghiệm duy nhất sao cho biểu thức đạt giá trị nhỏ nhất.
Hướng dẫn giải:
Xét hệ phương trình
Nhân hai vế của phương trình với 2, ta được hệ phương trình mới
Cộng hai vế của hai phương trình trên của hệ phương trình mới, ta được:
suy ra
Thay vào phương trình , ta được suy ra
Do đó với mọi giá trị m, hệ phương trình nghiệm duy nhất là
Dấu “=” xảy ra khi và chỉ khi hay
Vậy biểu thức P đạt giá trị nhỏ nhất bằng khi
III. BÀI TẬP TỰ LUYỆN
Bài 1. Cho hệ phương trình
Tìm m và n để hệ phương trình nhận cặp số là nghiệm.
Bài 2. Giải và biện luận theo tham số hệ phương trình
................................
................................
................................
Xem thêm các chuyên đề ôn thi vào lớp 10 môn Toán năm 2026 có đáp án hay khác:
Để học tốt lớp 10 các môn học sách mới:
- Giải bài tập Lớp 10 Kết nối tri thức
- Giải bài tập Lớp 10 Chân trời sáng tạo
- Giải bài tập Lớp 10 Cánh diều
Tủ sách VIETJACK luyện thi vào 10 cho 2k11 (2026):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Loạt bài Đề thi vào lớp 10 môn Toán (có đáp án) được các Giáo viên hàng đầu biên soạn theo cấu trúc ra đề thi Trắc nghiệm, Tự luận mới giúp bạn ôn luyện và giành được điểm cao trong kì thi vào lớp 10 môn Toán.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giáo án lớp 9 (các môn học)
- Giáo án điện tử lớp 9 (các môn học)
- Giáo án Toán 9
- Giáo án Ngữ văn 9
- Giáo án Tiếng Anh 9
- Giáo án Khoa học tự nhiên 9
- Giáo án Vật Lí 9
- Giáo án Hóa học 9
- Giáo án Sinh học 9
- Giáo án Địa Lí 9
- Giáo án Lịch Sử 9
- Giáo án GDCD 9
- Giáo án Tin học 9
- Giáo án Công nghệ 9
- Đề thi lớp 9 (các môn học)
- Đề thi Ngữ Văn 9 (có đáp án)
- Đề thi Toán 9 (có đáp án)
- Đề thi Tiếng Anh 9 mới (có đáp án)
- Đề thi Tiếng Anh 9 (có đáp án)
- Đề thi Khoa học tự nhiên 9 (có đáp án)
- Đề thi Lịch Sử và Địa Lí 9 (có đáp án)
- Đề thi GDCD 9 (có đáp án)
- Đề thi Tin học 9 (có đáp án)
- Đề thi Công nghệ 9 (có đáp án)


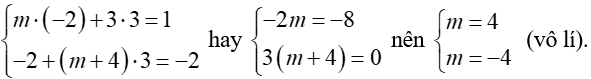








 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

