50+ Đề thi vào 10 Toán Chuyên năm 2025 (các năm có đáp án)
Nhằm mục đích giúp học sinh ôn thi chuyên Toán vào lớp 10 năm 2025, VietJack tổng hợp đề thi tuyển sinh vào lớp 10 Toán hệ chuyên chọn lọc, có đáp án được sưu tầm từ các trường chuyên trên cả nước. Hi vọng qua bộ đề ôn thi chuyên Toán này sẽ giúp bạn tìm hiểu về cấu trúc đề thi, từ đó ra kế hoạch ôn tập & đạt được kết quả cao trong kì thi tuyển sinh vào lớp 10 Toán chuyên.
50+ Đề thi vào 10 Toán Chuyên năm 2025 (các năm có đáp án)
Bộ đề ôn thi môn Toán vào 10 Chuyên gồm 23 đề thi tuyển sinh chuyên Toán vào 10 CÓ LỜI GIẢI và Bộ 200 Đề thi vào lớp 10 chuyên Toán ((năm 2022 và các năm trước - sưu tầm từ các trường chuyên trên cả nước) giúp Giáo viên có thêm tài liệu ôn thi Toán vào 10 hệ Chuyên.
Xem thử Bộ đề ôn Toán Chuyên Xem thử Bộ đề Toán 8+
Chỉ từ 150k mua trọn bộ đề thi bản word có lời giải chi tiết:
- B1: gửi phí vào tk:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án
Đề thi tuyển sinh vào 10 Toán Chuyên 2025
Đề thi tuyển sinh Toán vào lớp 10 Chuyên Tin năm 2025 tỉnh Hà Nội
Đề thi tuyển sinh Toán vào lớp 10 Chuyên trường THPT Chuyên Hạ Long - Quảng Ninh
Đề thi tuyển sinh Toán vào lớp 10 Chuyên trường THPT Chuyên Hùng Vương - Gia Lai
Đề thi tuyển sinh Toán vào lớp 10 Chuyên trường THPT Chuyên Phan Bội Châu - Nghệ An
Đề thi tuyển sinh Toán vào lớp 10 trường THPT chuyên KHTN Hà Nội (vòng 1)
Đề thi tuyển sinh Toán vào lớp 10 Chung trường THPT Chuyên Khoa học xã hội và nhân văn
Đề thi tuyển sinh Toán vào lớp 10 (không chuyên) năm 2025 trường Phổ thông năng khiếu HCM
Đề thi tuyển sinh Toán vào lớp 10 Chuyên trường Phổ thông năng khiếu HCM
Đề thi tuyển sinh Toán vào lớp 10 Chuyên trường THPT chuyên Khoa học Huế (vòng 1)
Đề thi tuyển sinh Toán vào lớp 10 trường THPT chuyên KHTN Hà Nội (vòng 2)
Đề thi tuyển sinh Toán vào lớp 10 Chuyên trường THPT Chuyên Hùng Vương - Phú Thọ
Đề thi tuyển sinh Toán vào lớp 10 trường THPT chuyên Đại học Vinh - Nghệ An (vòng 2)
Đề thi tuyển sinh vào 10 Toán Chuyên 2024
- Đề thi vào 10 Toán chuyên Lam Sơn (Thanh Hóa) năm 2024
- Đề thi vào 10 Toán chuyên Phổ thông năng khiếu năm 2024
- Đề thi vào 10 Toán chuyên Kiên Giang năm 2024
- Đề thi vào 10 Toán chuyên Vĩnh Phúc năm 2024
- Đề thi vào 10 Toán chuyên Tuyên Quang năm 2024
- Đề thi vào 10 Toán chuyên Yên Bái năm 2024
- Đề thi vào 10 Toán chuyên Thừa Thiên Huế năm 2024
- Đề thi vào 10 Toán chuyên Sóc Trăng năm 2024
- Đề thi vào 10 Toán chuyên Lê Quý Đôn (Đà Nẵng) năm 2024
- Đề thi vào 10 Toán chuyên Hưng Yên năm 2024
- Đề thi vào 10 Toán chuyên Hà Tĩnh năm 2024
- Đề thi vào 10 Toán chuyên Bà Rịa - Vũng Tàu năm 2024
- Đề thi vào 10 Toán chuyên TP Hồ Chí Minh năm 2024
- Đề thi vào 10 Toán chuyên Hà Nội năm 2024
- Đề thi vào 10 Toán chuyên Lâm Đồng năm 2024
- Đề thi vào 10 Toán chuyên Thái Bình năm 2024
- Đề thi vào 10 Toán chuyên Bắc Ninh năm 2024
- Đề thi vào 10 Toán chuyên Bình Phước năm 2024
- Đề thi vào 10 Toán chuyên Phú Thọ năm 2024
- Đề thi vào 10 Toán chuyên Hải Phòng năm 2024
- Đề thi vào 10 Toán chuyên Hà Nam năm 2024
- Đề thi vào 10 Toán chuyên Sơn La năm 2024
- Đề thi vào 10 Toán chuyên Phú Yên năm 2024
- Đề thi vào 10 Toán chuyên Bình Định năm 2024
- Đề thi vào 10 Toán chuyên Đà Nẵng năm 2024
- Đề thi vào 10 Toán chuyên Huỳnh Mẫn Đạt (Kiên Giang) năm 2024
Đề thi tuyển sinh vào 10 Toán Chuyên 2023
- Đề thi tuyển sinh vào lớp 10 Toán Chuyên Lam Sơn (Thanh Hóa) năm 2023
- Đề thi tuyển sinh vào lớp 10 Toán Chuyên Bạc Liêu năm 2023
- Đề thi tuyển sinh vào lớp 10 Toán Chuyên Hà Nam năm 2023
- Đề thi tuyển sinh vào lớp 10 Toán Chuyên Nam Định năm 2023
- Đề thi tuyển sinh vào lớp 10 Toán Chuyên ĐH Sư phạm Hà Nội năm 2023
- Đề thi tuyển sinh vào lớp 10 Toán Chuyên ĐH Khoa học Huế năm 2023
- Đề thi tuyển sinh vào lớp 10 Toán chuyên Phú Yên năm 2023
- Đề thi tuyển sinh vào lớp 10 Toán chuyên Kiên Giang năm 2023
- Đề thi tuyển sinh vào lớp 10 Toán chuyên Quảng Trị năm 2023
- Đề thi tuyển sinh vào lớp 10 Toán chuyên Hạ Long (Quảng Ninh) năm 2023
- Đề thi tuyển sinh vào lớp 10 Toán chuyên Trà Vinh năm 2023
- Đề thi tuyển sinh vào lớp 10 Toán chuyên Tây Ninh năm 2023
- Đề thi tuyển sinh vào lớp 10 Toán chuyên Ninh Bình năm 2023
- Đề thi tuyển sinh vào lớp 10 Toán chuyên Yên Bái năm 2023
- Đề thi tuyển sinh vào lớp 10 Toán chuyên An Giang năm 2023
- Đề thi tuyển sinh vào lớp 10 Toán chuyên Hải Dương năm 2023
- Đề thi tuyển sinh vào lớp 10 Toán chuyên Hưng Yên năm 2023
- Đề thi tuyển sinh vào lớp 10 Toán chuyên Tp Hải Phòng năm 2023
- Đề thi tuyển sinh vào lớp 10 Toán chuyên Tp Đà Nẵng năm 2023
- Đề thi tuyển sinh vào lớp 10 Toán chuyên Hòa Bình năm 2023
- Đề thi tuyển sinh vào lớp 10 Toán chuyên Bình Phước năm 2023
- Đề thi tuyển sinh vào lớp 10 Toán chuyên Hà Tĩnh năm 2023
- Đề thi tuyển sinh vào lớp 10 Toán chuyên Lào Cai năm 2023
- Đề thi tuyển sinh vào lớp 10 Toán chuyên Kom Tum năm 2023
- Đề thi tuyển sinh vào lớp 10 Toán chuyên Thái Nguyên năm 2023
- Đề thi tuyển sinh vào lớp 10 Toán chuyên Tin Thái Nguyên năm 2023
- Đề thi tuyển sinh vào lớp 10 Toán chuyên Phan Bội Châu (Nghệ An) năm 2023
- Đề thi tuyển sinh vào lớp 10 Toán chuyên Đắk Nông năm 2023
Đề thi tuyển sinh vào 10 Toán Chuyên (các năm)
Đề thi tuyển sinh vào lớp 10 Toán chuyên Phan Bội Châu năm 2012-2013
Đề thi tuyển sinh vào lớp 10 Toán chuyên Hùng Vương năm 2015-2016
Đề thi tuyển sinh vào lớp 10 Toán chuyên Vĩnh Phúc năm 2016-2017
Đề thi tuyển sinh vào lớp 10 Toán chuyên Nguyễn Trãi năm 2015-2016
Đề thi tuyển sinh vào lớp 10 Toán chuyên Thành Phố Hồ Chí Minh
Đề thi tuyển sinh vào lớp 10 Toán chuyên Năng Khiếu Trần Phú
Đề thi tuyển sinh vào lớp 10 Toán chuyên Bình Phước năm 2013-2014
Đề thi tuyển sinh vào lớp 10 Toán chuyên Hùng Vương năm 2009-2010
Đề thi tuyển sinh vào lớp 10 Toán chuyên Hoàng Văn Thụ năm 2013-2014
Đề thi tuyển sinh vào lớp 10 Toán chuyên TP Hồ Chí Minh năm 2008-2009
Đề thi tuyển sinh vào lớp 10 Toán chuyên Bà Rịa - Vũng Tàu năm 2016-2017
Đề thi tuyển sinh vào lớp 10 Toán chuyên Hà Nội năm 2009-2010
Đề thi tuyển sinh vào lớp 10 Toán chuyên Lạng Sơn năm 2013-2014
Xem thử Bộ đề ôn Toán Chuyên Xem thử Bộ đề Toán 8+
Sở Giáo dục và Đào tạo Hà Nội
Trường Đại học Sư phạm Hà Nội
Kì thi tuyển sinh vào lớp 10 THPT chuyên
Đề thi môn: Toán
Năm học: ......
Thời gian: 150 phút (không kể thời gian giao đề)
Câu 1 (2 điểm): Cho biểu thức 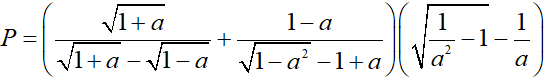
Câu 2 (2,5 điểm): Cho parabol (P): y=-x2 và đường thẳng d:y=2mx-1 với m là tham số.
a) Tìm tọa độ giao điểm của d và (P) khi m=1 .
b) Chứng minh rằng với mỗi giá trị của m, d luôn cắt (P) tại hai điểm phân biệt A, B. Gọi y1, y2 là tung độ của A, B. Tìm m sao cho
Câu 3 (1,5 điểm): Một người đi xe máy từ địa điểm A đến địa điểm B cách nhau 120 km. Vận tốc trên 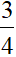
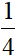

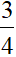
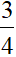
Câu 4 (3 điểm): Cho ba điểm A, M, B phân biệt, thẳng hàng và M nằm giữa A, B. Trên cùng một nửa mặt phẳng bờ là đường thẳng AB, dựng hai tam giác đều AMC và BMD. Gọi P là giao điểm của AD và BC.
a) Chứng minh AMPC và BMPD là các tứ giác nội tiếp
b) Chứng minh
c) Đường thẳng nối tâm của hai đường tròn ngoại tiếp hai tứ giác AMPC và BMPD cắt PA, PB tương ứng tại E, F. Chứng minh CDFE là hình thang.
Câu 5 (1 điểm): Cho a, b, c là ba số thực không âm và thỏa mãn: a + b + c = 1. Chứng minh rằng:
Sở Giáo dục và Đào tạo Nghệ An
Trường THPT Chuyên Phan Bội Châu
Kì thi tuyển sinh vào lớp 10 THPT chuyên
Đề thi môn: Toán
Năm học: ......
Thời gian: 150 phút (không kể thời gian giao đề)
Câu 1 (7 điểm):
a) Giải phương trình:
b) Giải hệ phương trình:
Câu 2 (3 điểm): Tìm các số tự nhiên x và y thoả mãn 2x+1=y2
Câu 3 (2 điểm): Cho ba số dương x,y,z thoả mãn 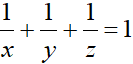
Câu 4 (6 điểm): Cho đường tròn tâm O, đường kính AB. Trên đường tròn lấy điểm D khác A và 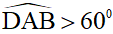
a) Chứng minh tứ giác AFCN nội tiếp đường tròn và ba điểm N, C, E thẳng hàng.
b) Cho AD = BC, chứng minh DN đi qua trung điểm của AC.
Câu 5 (2 điểm): Một tứ giác lồi có độ dài bốn cạnh đều là số tự nhiên sao cho tổng ba số bất kì trong chúng chia hết cho số còn lại. Chứng minh rằng tứ giác đó có ít nhất hai cạnh bằng nhau.
Sở Giáo dục và Đào tạo Phú Thọ
Trường THPT Chuyên Hùng Vương
Kì thi tuyển sinh vào lớp 10 THPT chuyên
Đề thi môn: Toán
Năm học: ......
Thời gian: 150 phút (không kể thời gian giao đề)
Câu 1 (1,5 điểm):
a) Chứng minh rằng nếu số nguyên n lớn hơn 1 thoả mãn n2+4 và n2+16 là các số nguyên tố thì n chia hết cho 5.
b) Tìm nghiệm nguyên của phương trình: x2-2y(x-y)=2(x+1)
Câu 2 (2 điểm):
a) Rút gọn biểu thức:
b) Tìm m để phương trình: (x-2)(x-3)(x+4)(x+5)=m có 4 nghiệm phân biệt.
Câu 3 (2 điểm):
a) Giải phương trình:
b) Giải hệ phương trình:
Câu 4 (3,5 điểm): Cho đường tròn (O; R) và dây cung 
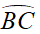
a) Chứng minh KA là phân giác trong góc 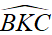
b) Xác định vị trí điểm A để diện tích tứ giác BHCK lớn nhất, tính diện tích lớn nhất của tứ giác đó theo R.
c) Chứng minh AK luôn đi qua một điểm cố định.
Câu 5 (1,0 điểm): Cho 3 số thực dương x,y,z thoả mãn 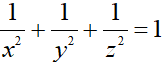
Xem thử Bộ đề ôn Toán Chuyên Xem thử Bộ đề Toán 8+
Để học tốt lớp 10 các môn học sách mới:
- Giải bài tập Lớp 10 Kết nối tri thức
- Giải bài tập Lớp 10 Chân trời sáng tạo
- Giải bài tập Lớp 10 Cánh diều
Tủ sách VIETJACK luyện thi vào 10 cho 2k11 (2026):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Loạt bài Đề thi vào lớp 10 môn Toán (có đáp án) được các Giáo viên hàng đầu biên soạn theo cấu trúc ra đề thi Trắc nghiệm, Tự luận mới giúp bạn ôn luyện và giành được điểm cao trong kì thi vào lớp 10 môn Toán.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giáo án lớp 9 (các môn học)
- Giáo án điện tử lớp 9 (các môn học)
- Giáo án Toán 9
- Giáo án Ngữ văn 9
- Giáo án Tiếng Anh 9
- Giáo án Khoa học tự nhiên 9
- Giáo án Vật Lí 9
- Giáo án Hóa học 9
- Giáo án Sinh học 9
- Giáo án Địa Lí 9
- Giáo án Lịch Sử 9
- Giáo án GDCD 9
- Giáo án Tin học 9
- Giáo án Công nghệ 9
- Đề thi lớp 9 (các môn học)
- Đề thi Ngữ Văn 9 (có đáp án)
- Đề thi Toán 9 (có đáp án)
- Đề thi Tiếng Anh 9 mới (có đáp án)
- Đề thi Tiếng Anh 9 (có đáp án)
- Đề thi Khoa học tự nhiên 9 (có đáp án)
- Đề thi Lịch Sử và Địa Lí 9 (có đáp án)
- Đề thi GDCD 9 (có đáp án)
- Đề thi Tin học 9 (có đáp án)
- Đề thi Công nghệ 9 (có đáp án)

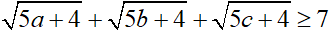
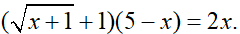
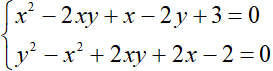
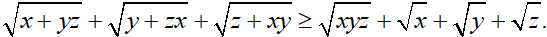
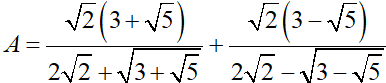
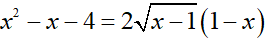
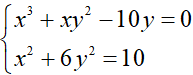
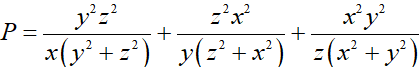






 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

