30+ Đề thi tuyển sinh vào lớp 10 Toán Hà Nội 2025 (có đáp án)
Để giành được điểm cao trong bài thi tuyển sinh môn Toán vào lớp 10 Hà Nội năm 2025, dưới đây là các đề thi thử vào lớp 10 môn Toán có đáp án. Bạn vào tên đề thi hoặc Xem đề thi để tham khảo đề thi vào 10 môn Toán và phần đáp án tương ứng.
30+ Đề thi tuyển sinh vào lớp 10 Toán Hà Nội 2025 (có đáp án)
Bộ đề thi vào 10 môn Toán Hà Nội gồm 8 đề thi CHÍNH THỨC từ năm 2015 → 2024 có lời giải chi tiết giúp Giáo viên có thêm tài liệu ôn thi Toán vào 10 Hà Nội:
Xem thử Bộ đề thi thử vào 10 Toán 2025 Xem thử Bộ đề thi vào 10 Toán 2025 Xem thử Đề vào 10 Hà Nội
Chỉ từ 150k mua trọn bộ Đề ôn thi vào 10 môn Toán năm 2026 theo cấu trúc mới bản word có lời giải chi tiết:
- B1: gửi phí vào tk:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận đề thi
Đề thi vào lớp 10 Toán Hà Nội 2025
Đề thi tuyển sinh Toán vào lớp 10 Chuyên Tin năm 2025 tỉnh Hà Nội
Đề thi tuyển sinh Toán vào lớp 10 trường THPT chuyên KHTN Hà Nội (vòng 1)
Đề thi tuyển sinh Toán vào lớp 10 Chung trường THPT Chuyên Khoa học xã hội và nhân văn
- Đề minh họa Toán vào lớp 10 Hà Nội 2025
- Đề thi tuyển sinh vào 10 môn Toán Hà Nội năm 2025
- Đề minh họa vào 10 Toán Hà Nội 2024
- Đề thi tuyển sinh vào 10 môn Toán Hà Nội năm 2023
- Cấu trúc đề thi vào lớp 10 môn Toán năm 2025 Hà Nội
- Bộ Đề thi thử vào 10 môn Toán năm 2025 (cả nước)
- Bộ Đề ôn thi vào 10 môn Toán năm 2025 có đáp án (Trắc nghiệm - Tự luận)
Đề thi thử Toán vào 10 năm 2026 (cả nước)
Đề thi thử Toán vào lớp 10 năm 2025 trường THCS Nguyễn Trường Tộ
Đề thi thử Toán vào lớp 10 năm 2025 trường TH&THCS Hồ Tùng Mậu
Xem thử Bộ đề thi thử vào 10 Toán 2025 Xem thử Bộ đề thi vào 10 Toán 2025 Xem thử Đề vào 10 Hà Nội
Đề luyện thi Toán vào lớp 10 Hà Nội 2026 - Đề 2
|
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI ĐỀ THAM KHẢO |
KỲ THI TUYỂN SINH LỚP 10 THEO CHƯƠNG TRÌNH GDPT 2018 MÔN: TOÁN 9 Thời gian: 120 phút, không kể thời gian giao đề. |
ĐỀ BÀI
Câu I: (1,5 điểm)
1) Cho bảng tần số ghép nhóm sau về tuổi thọ của một số ong mật cái như sau:
|
Tuổi thọ (ngày) |
[30; 40) |
[40; 50) |
[50; 60) |
|
Tần số |
14 |
24 |
22 |
Tìm tần số ghép nhóm và tần số tương đối ghép nhóm của nhóm [40; 50).
2) Trong một hộp đựng 15 tấm thẻ đánh số từ 1 đến 15 và không có hai tấm thẻ nào đánh số trùng nhau. An rút ngẫu nhiên một tấm thẻ trong hộp. Tính xác suất của biến cố A: “An rút được tấm thẻ đánh số chia hết cho 3 và không vượt quá 10”.
Câu II: (1,5 điểm) Cho hai biểu thức M = và N = với x > 0; x ≠ 4
1) Tính giá trị biểu thức của M khi x = 9.
2) Rút gọn biểu thức N.
3) Tìm giá trị của x để biểu thức đạt giá trị nhỏ nhất.
Câu III: (2,5 điểm)
1) Một cửa hàng thời trang trong một quý đã nhập hàng với tổng số vốn là 800 triệu và bán hết hàng trong quý đó. Cửa hàng gồm 2 loại thời trang nam và thời trang nữ. Biết thời trang nam lãi 15% và thời trang nữ lãi 20%, tổng số tiền lãi của quí đó là 145 triệu đồng. Tính số vốn cửa hàng đã nhập cho mỗi loại thời trang trên.
2) Một ô tô và một xe máy cùng khởi hành từ A để đi đến B với vận tốc của mỗi xe không đổi trên toàn bộ quãng đường AB dài 120km. Do vận tốc xe ô tô lớn hơn vận tốc xe máy là 10km/h nên xe ô tô đến B sớm hơn xe máy là 36 phút. Tính vận tốc của mỗi xe.
3) Cho phương trình x2 - x - 3 = 0 có hai nghiệm x1, x2. Không giải phương trình, hãy tính giá trị của biểu thức A =
Câu IV: (4,0 điểm)
1) Một hộp đựng bóng tennis có dạng hình trụ chứa vừa khít 3 quả bóng tennis xếp theo chiều dọc như hình bên. Các quả bóng có dạng hình cầu, đường kính 6,8cm.
a) Tính thể tích hộp đựng bóng (bỏ qua bề dày của vỏ hộp, lấy và làm tròn kết quả đến hàng đơn vị của cm3).
b) Tính thể tích bên trong hộp đựng bóng không bị chiếm bởi 3 quả bóng tennis (lấy và làm tròn kết quả đến hàng đơn vị của cm3).
2) Cho nửa đường tròn (O) đường kính AB. Điểm M nằm trên nửa đường tròn (M ≠ A; B). Tiếp tuyến tại M cắt tiếp tuyến tại A và B của đường tròn (O) lần lượt tại C và D.
a) Chứng minh rằng: tứ giác ACMO nội tiếp.
b) Gọi P là giao điểm CD và AB. Chứng minh: PA.PO = PC.PM
c) Gọi E là giao điểm của AM và BD; F là giao điểm của AC và BM. Chứng minh: E; F; P thẳng hàng.
Câu V: (0,5 điểm) Cho một tấm nhôm hình vuông cạnh 12 cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x ( cm), rồi gấp tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm x để thể tích của hộp là lớn nhất.
HẾT
Đề thi tuyển sinh Toán vào lớp 10 Hà Nội năm 2025
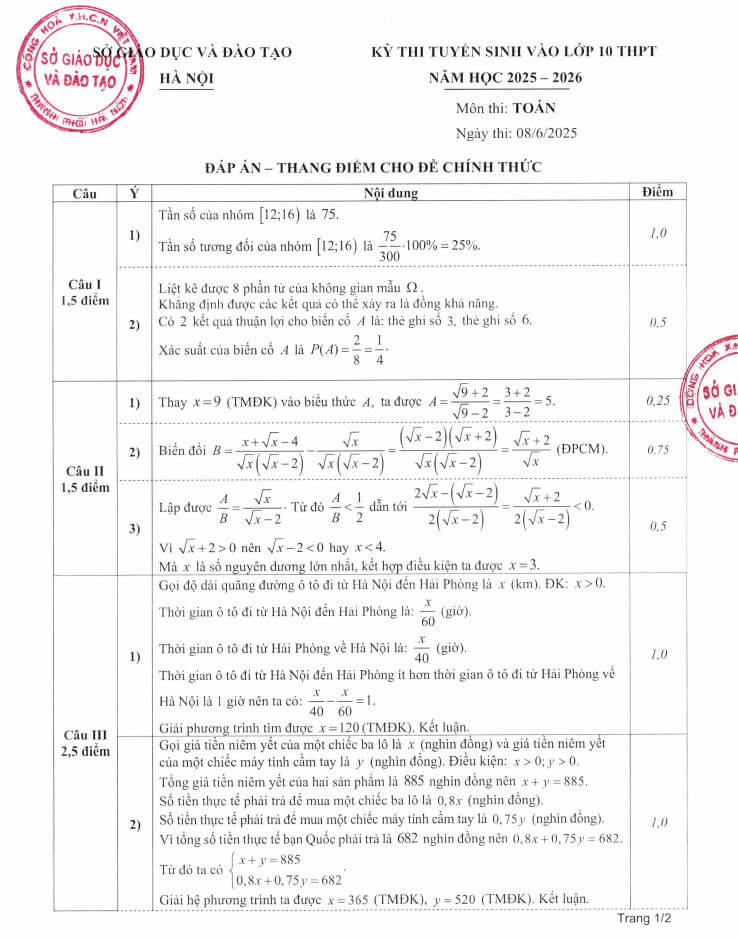
Đáp án Đề thi Toán vào lớp 10 năm 2025 tỉnh Hà Nội
Đề thi minh họa Toán vào lớp 10 Hà Nội 2025
Sở Giáo dục và Đào tạo Hà Nội
Đề minh họa kỳ thi tuyển sinh lớp 10 THPT theo chương trình GDPT 2018
Môn thi: Toán
Thời gian làm bài: 120 phút
Đáp án tham khảo Đề thi minh họa Toán vào lớp 10 Hà Nội 2025
Đề thi tuyển sinh vào 10 Toán Hà Nội 2024
Đáp án đề thi Toán vào 10 Hà Nội 2024
Xem thử Bộ đề thi thử vào 10 Toán 2025 Xem thử Bộ đề thi vào 10 Toán 2025 Xem thử Đề vào 10 Hà Nội
Xem thêm các đề thi vào lớp 10 môn Toán có đáp án hay khác:
- Bộ Đề thi vào lớp 10 môn Toán năm 2021 - 2022 có đáp án (Trắc nghiệm - Tự luận)
- Bộ Đề thi vào lớp 10 môn Toán năm 2021 - 2022 có đáp án (Tự luận)
- Tổng hợp Đề thi vào lớp 10 chuyên Toán
Xem thêm đề thi lớp 9 các môn học có đáp án hay khác:
Tài liệu giáo án lớp 9 các môn học chuẩn khác:
Để học tốt lớp 10 các môn học sách mới:
- Giải bài tập Lớp 10 Kết nối tri thức
- Giải bài tập Lớp 10 Chân trời sáng tạo
- Giải bài tập Lớp 10 Cánh diều
Tủ sách VIETJACK luyện thi vào 10 cho 2k11 (2026):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Loạt bài Đề thi vào lớp 10 môn Toán (có đáp án) được các Giáo viên hàng đầu biên soạn theo cấu trúc ra đề thi Trắc nghiệm, Tự luận mới giúp bạn ôn luyện và giành được điểm cao trong kì thi vào lớp 10 môn Toán.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giáo án lớp 9 (các môn học)
- Giáo án điện tử lớp 9 (các môn học)
- Giáo án Toán 9
- Giáo án Ngữ văn 9
- Giáo án Tiếng Anh 9
- Giáo án Khoa học tự nhiên 9
- Giáo án Vật Lí 9
- Giáo án Hóa học 9
- Giáo án Sinh học 9
- Giáo án Địa Lí 9
- Giáo án Lịch Sử 9
- Giáo án GDCD 9
- Giáo án Tin học 9
- Giáo án Công nghệ 9
- Đề thi lớp 9 (các môn học)
- Đề thi Ngữ Văn 9 (có đáp án)
- Đề thi Toán 9 (có đáp án)
- Đề thi Tiếng Anh 9 mới (có đáp án)
- Đề thi Tiếng Anh 9 (có đáp án)
- Đề thi Khoa học tự nhiên 9 (có đáp án)
- Đề thi Lịch Sử và Địa Lí 9 (có đáp án)
- Đề thi GDCD 9 (có đáp án)
- Đề thi Tin học 9 (có đáp án)
- Đề thi Công nghệ 9 (có đáp án)
















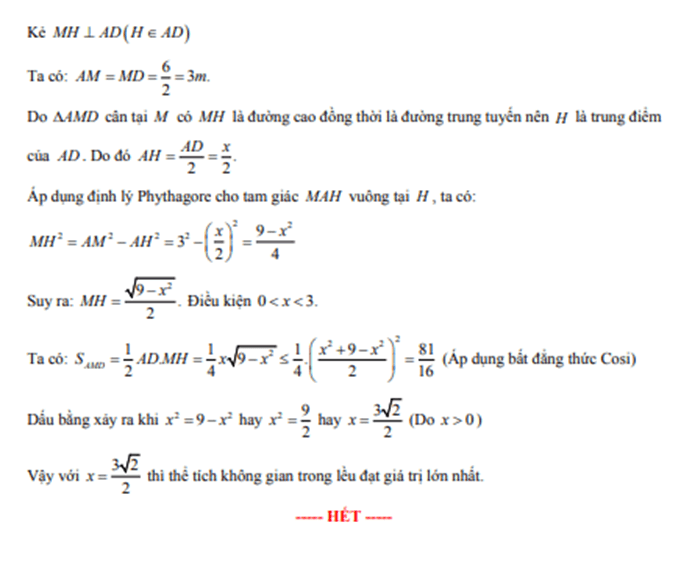













 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

