Không giải phương trình, hãy tính tổng và tích các nghiệm (nếu có) của mỗi phương trình sau

Bài 6: Hệ thức Vi-ét và ứng dụng

Luyện tập trang 54 sgk Toán lớp 9 Tập 2

Video Bài 29 trang 54 SGK Toán 9 Tập 2 - Cô Ngô Hoàng Ngọc Hà (Giáo viên VietJack)

Bài 29 trang 54 SGK Toán lớp 9 Tập 2: Không giải phương trình, hãy tính tổng và tích các nghiệm (nếu có) của mỗi phương trình sau:

Quảng cáo

a) 4x² + 2x – 5 = 0;

b) 9x² – 12x + 4 = 0;

c) 5x² + x + 2 = 0;

d) 159x² – 2x – 1 = 0.

Lời giải

a) Phương trình 4x² + 2x – 5 = 0

Có a = 4; b = 2; c = -5, a.c < 0

⇒ Phương trình có hai nghiệm x₁; x₂

Theo hệ thức Vi-et ta có: 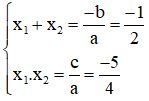Giải bài tập Vật lý lớp 12 nâng cao

Quảng cáo

b) Phương trình 9x² – 12x + 4 = 0

Có a = 9; b' = -6; c = 4 ⇒ Δ’ = (-6)² – 4.9 = 0

⇒ Phương trình có nghiệm kép x₁ = x₂.

Theo hệ thức Vi-et ta có: 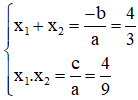Giải bài tập Vật lý lớp 12 nâng cao

c) Phương trình 5x² + x + 2 = 0

Có a = 5; b = 1; c = 2 ⇒ Δ = 1² – 4.2.5 = -39 < 0

⇒ Phương trình vô nghiệm.

d) Phương trình 159x² – 2x – 1 = 0

Có a = 159; b = -2; c = -1; a.c < 0

⇒ Phương trình có hai nghiệm phân biệt x₁; x₂.

Theo hệ thức Vi-et ta có: 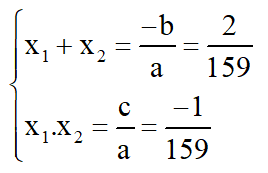Giải bài tập Vật lý lớp 12 nâng cao

Kiến thức áp dụng

Phương trình bậc hai ax² + bx + c = 0, có Δ = b² – 4ac.

+ Nếu Δ < 0, phương trình vô nghiệm.

+ Nếu Δ ≥ 0, phương trình có hai nghiệm x₁; x₂ thỏa mãn hệ thức Vi-et:

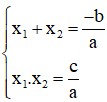
Lưu ý: Trước khi áp dụng hệ thức Vi-et, bắt buộc phải kiểm tra Δ xem phương trình có nghiệm hay không.

Phương trình bậc hai ax² + bx + c = 0 có a và c trái dấu, tức là a.c < 0 thì luôn có hai nghiệm phân biệt.

Quảng cáo

Xem thêm các bài giải bài tập Toán lớp 9 Bài 6 khác:

bai-6-he-thuc-viet-va-ung-dung.jsp

Giải bài tập lớp 9 sách mới các môn học

Học cùng VietJack

Chính sách