Giải bài tập Toán lớp 9 Bài 1: Căn bậc hai
Trả lời câu hỏi Toán 9 Tập 1 Bài 1 trang 4
: Tìm các căn bậc hai của mỗi số sau:
a) 9; b) 4/9; c) 0,25; d) 2.
Lời giải
a) Căn bậc hai của 9 là 3 và -3 (vì 32 = 9 và (-3)2 = 9)
b) Căn bậc hai của 4/9 là 2/3 và (-2)/3 (vì (2/3)2 = 4/9 và(-2/3)2 = 4/9)
c) Căn bậc hai của 0,25 là 0,5 và -0,5 (vì 0,52 = 0,25 và (-0,5)2 = 0,25)
d) Căn bậc hai của 2 là √2 và -√2 (vì (√2)2 = 2 và(-√2)2 = 2 )
Trả lời câu hỏi Toán 9 Tập 1 Bài 1 trang 5
: Tìm căn bậc hai số học của mỗi số sau:
a) 49; b) 64; c) 81; d) 1,21.
Lời giải
a) √49 = 7, vì 7 > 0 và 72 = 49
b) √64 = 8, vì 8 > 0 và 82 = 64
c) √81 = 9, vì 9 > 0 và 92 = 81
d) √1,21 = 1,1 vì 1,1 > 0 và 1,12 = 1,21
Trả lời câu hỏi Toán 9 Tập 1 Bài 1 trang 5
: Tìm căn bậc hai của mỗi số sau:
a) 64; b) 81; c) 1,21.
Lời giải
a) Các căn bậc hai của 64 là 8 và -8
b) Các căn bậc hai của 81 là 9 và -9
c) Các căn bậc hai của 1,21 là 1,1 và -1,1
Trả lời câu hỏi Toán 9 Tập 1 Bài 1 trang 6
: So sánh
a) 4 và √15; b) √11 và 3.
Lời giải
a) 16 > 15 nên √16 > √15. Vậy 4 > √15
b) 11 > 9 nên √11 > √9. Vậy √11 > 3
Trả lời câu hỏi Toán 9 Tập 1 Bài 1 trang 6
: Tìm số x không âm, biết:
a) √x > 1; b) √x < 3.
Lời giải
a) 1 = √1, nên √x > 1 có nghĩa là √x > √1
Vì x ≥ 0 nên √x > √1 ⇔ x > 1. Vậy x > 1
b) 3 = √9, nên √x < 3 có nghĩa là √x < √9
Vì x ≥ 0 nên √x < √9 ⇔ x < 9. Vậy x < 9
Bài 1 trang 6 SGK Toán lớp 9 Tập 1:
Tìm căn bậc hai số học của mỗi số sau rồi suy ra căn bậc hai của chúng:
121; 144; 169; 225; 256; 324; 361; 400
Lời giải:
Ta có: √121 = 11 vì 11 > 0 và 112 = 121 nên
Căn bậc hai số học của 121 là 11. Căn bậc hai của 121 là 11 và – 11.
Tương tự:
Căn bậc hai số học của 144 là 12. Căn bậc hai của 144 là 12 và -12.
Căn bậc hai số học của 169 là 13. Căn bậc hai của 169 là 13 và -13.
Căn bậc hai số học của 225 là 15. Căn bậc hai của 225 là 15 và -15.
Căn bậc hai số học của 256 là 16. Căn bậc hai của 256 là 16 và -16.
Căn bậc hai số học của 324 là 18. Căn bậc hai của 324 là 18 và -18.
Căn bậc hai số học của 361 là 19. Căn bậc hai của 361 là 19 và -19.
Căn bậc hai số học của 400 là 20. Căn bậc hai của 400 là 20 và -20.
Bài 2 trang 6 SGK Toán lớp 9 Tập 1:
So sánh:
a) 2 và √3 ; b) 6 và √41 ; c) 7 và √47
a) 2 = √4
Vì 4 > 3 nên √4 > √3 (định lí)
Vậy 2 > √3
b) 6 = √36
Vì 36 < 41 nên √36 < √41
Vậy 6 < √41
c) 7 = √49
Vì 49 > 47 nên √49 > √47
Vậy 7 > √47
Bài 3 trang 6 SGK Toán lớp 9 Tập 1:
Dùng máy tính bỏ túi, tính giá trị gần đúng của nghiệm mỗi phương tình sau (làm tròn đến chữ số thập phân thứ ba):
a) x2 = 2 ; b) x2 = 3
c) x2 = 3,5 ; d) x2 = 4,12
Hướng dẫn: Nghiệm của phương trình x2 = a ( với a ≥ 0) là các căn bậc hai của a.
Lời giải:
a) x2 = 2 => x1 = √2 và x2 = -√2
Dùng máy tính bỏ túi ta tính được:
√2 ≈ 1,414213562
Kết quả làm tròn đến chữ số thập phân thứ ba là:
x1 = 1,414; x2 = - 1,414
b) x2 = 3 => x1 = √3 và x2 = -√3
Dùng máy tính ta được:
√3 ≈ 1,732050907
Vậy x1 = 1,732; x2 = - 1,732
c) x2 = 3,5 => x1 = √3,5 và x2 = -√3,5
Dùng máy tính ta được:
√3,5 ≈ 1,870828693
Vậy x1 = 1,871; x2 = - 1,871
d) x2 = 4,12 => x1 = √4,12 và x2 = -√4,12
Dùng máy tính ta được:
√4,12 ≈ 2,029778313
Vậy x1 = 2,030 ; x2 = - 2,030
Bài 4 trang 7 SGK Toán lớp 9 Tập 1:
Tìm số x không âm, biết:
a) √x = 15; b) 2√x = 14
c) √x < √2; d) √2x < 4
Lời giải:
Lưu ý: Vì x không âm (x ≥ 0) nên các căn thức trong bài đều xác định.
a) √x = 15
Vì x ≥ 0 nên bình phương hai vế ta được:
x = 152 ⇔ x = 225
Vậy x = 225
b) 2√x = 14 ⇔ √x = 7
Vì x ≥ 0 nên bình phương hai vế ta được:
x = 72 ⇔ x = 49
Vậy x = 49
c) √x < √2
Vì x ≥ 0 nên bình phương hai vế ta được: x < 2
Vậy 0 ≤ x < 2
<
d) 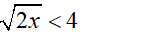
Vì x ≥ 0 nên bình phương hai vế ta được:
2x < 16 ⇔ x < 8
Vậy 0 ≤ x < 8
Bài 5 trang 7 SGK Toán lớp 9 Tập 1:
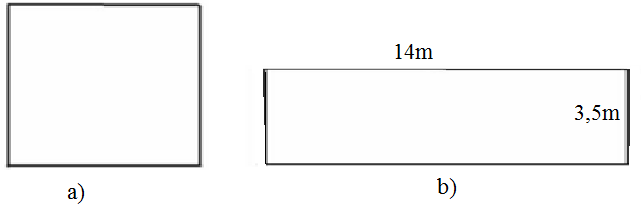
Đố. Tính cạnh một hình vuông, biết diện tích của nó bằng diện tích của hình chữ nhật có chiều rộng 3,5m và chiều dài 14m.
Hình 1
Lời giải:
Diện tích hình chữ nhật: SHCN = 3,5.14 = 49 (m2)
Gọi a (m) (a > 0) là độ dài của cạnh hình vuông. Suy ra diện tích hình vuông là
SHV = a2 = 49 (m2)
=> a = 7 (m)
Vậy cạnh hình vuông có độ dài là 7m.
Ghi chú: Nếu ta cắt đôi hình chữ nhật thành hai hình chữ nhật có kích thước 3,5m x 7m thì ta sẽ ghép được hình vuông có cạnh là 7m.
Giải bài tập Toán lớp 9 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông
Trả lời câu hỏi Toán 9 Tập 1 Bài 1 trang 66
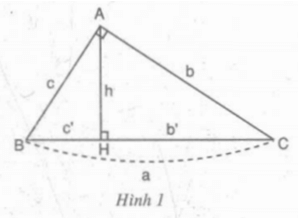
: Xét hình 1. Chứng minh ΔAHB ∼ ΔCHA. Từ đó suy ra hệ thức (2).
Lời giải
Xét ΔABH và ΔCAH có:
∠(AHB) = ∠(AHC) = 90o
∠(BAH) = ∠(ACH) (cùng phụ ∠(CAH))
⇒ ΔABH ∼ ΔCAH (g.g)
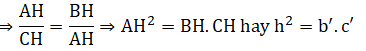
Trả lời câu hỏi Toán 9 Tập 1 Bài 1 trang 67
: Xét hình 1. Hãy chứng minh hệ thức (3) bằng tam giác đồng dạng.
Lời giải
Xét tam giác ABC vuông tại A có
SABC = 1/2 AB.AC
Xét tam giác ABC có AH là đường cao
⇒ SABC = 1/2 AH.BC
⇒ 1/2 AB.AC = 1/2 AH.BC ⇒ AB.AC = AH.BC hay bc = ah
Bài 1 trang 68 SGK Toán lớp 9 Tập 1:
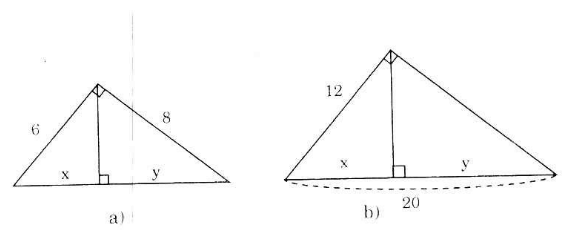
Hãy tính x và y trong mỗi hình sau: (h.4a, b)
Hình 4
Lời giải:
- Hình a
Theo định lí Pitago ta có:
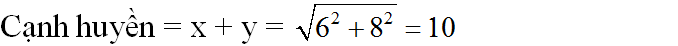
Áp dụng định lí 1 ta có:
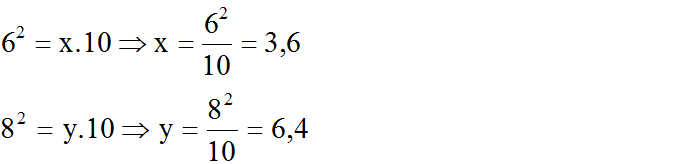
- Hình b
Áp dụng định lí 1 ta có:
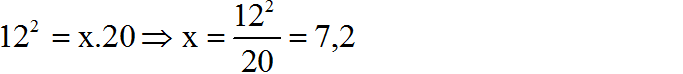
=> y = 20 - 7,2 = 12,8
Bài 2 trang 68 SGK Toán lớp 9 Tập 1:
Hãy tính x và y trong mỗi hình sau: (h.5)
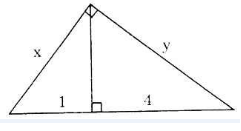
Hình 5
Lời giải:
Áp dụng định lí 1 ta có:
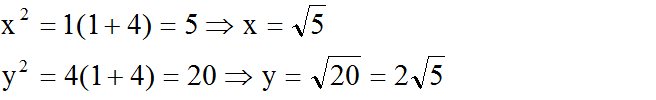
Bài 3 trang 69 SGK Toán lớp 9 Tập 1:
Hãy tính x và y trong mỗi hình sau: (h.6)
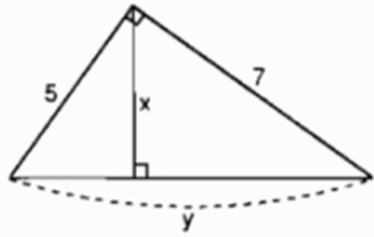
Hình 6
Lời giải:
Áp dụng định lí Pitago ta có:
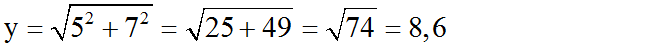
Áp dụng định lí 3 ta có:
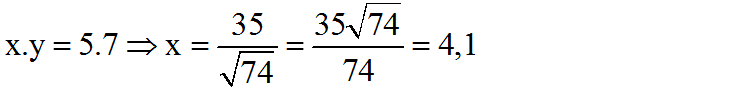
Bài 4 trang 69 SGK Toán lớp 9 Tập 1:
Hãy tính x và y trong mỗi hình sau: (h.7)
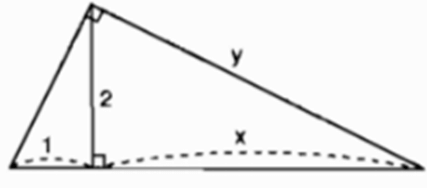
Hình 7
Lời giải:
Theo định lí 2 ta có:
22 = 1.x => x = 4
Theo định lí 1 ta có:
y2 = x(1 + x) = 4(1 + 4) = 20
=> y = √20 = 2√5

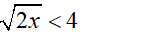


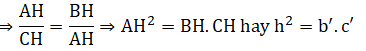

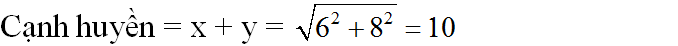
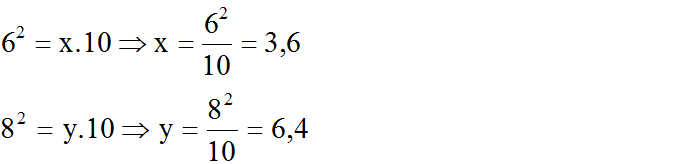
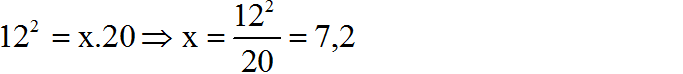

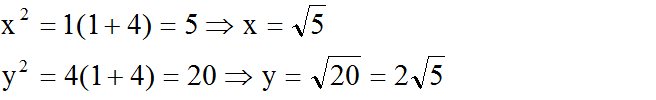

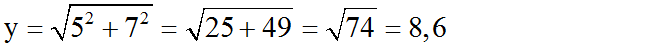
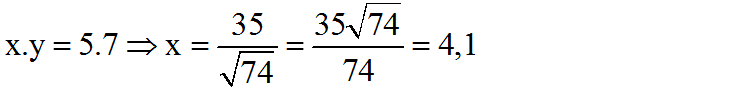




 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

