Câu hỏi ôn tập chương 3 phần Hình Học 9

---

---

Ôn tập chương 3 Phần Hình Học

Trả lời phần Câu hỏi trang 100-101 sgk Toán 9 Tập 2

1. Góc ở tâm là gì?

Trả lời:

Góc ở tâm là góc có đỉnh trùng với tâm của đường tròn.

2. Góc nội tiếp là gì?

Trả lời:

Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.

3. Góc tạo bởi tia tiếp tuyến và dây cung là gì?

Trả lời:

Góc tạo bởi tia tiếp tuyến và dây cung là góc có đỉnh tại tiếp điểm, một cạnh là tia tiếp tuyến, cạnh còn lại chứa dây cung. Ví dụ góc BAx trong hình.

Góc tạo bởi một tia tiếp tuyến với một dây cung của đường tròn có một đầu mút là gốc của tia tiếp tuyến gọi là góc tạo bởi tiếp tuyến và dây cung. Ví dụ góc Bax trong hình.

4. Tứ giác nội tiếp là gì?

Trả lời:

Tứ giác nội tiếp là tứ giác có 4 đỉnh nằm trên một đường tròn.

5. Với ba điểm A, B, C thuộc một đường tròn, khi nào thì

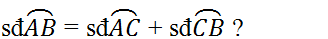
Trả lời:

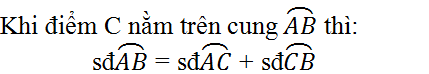
6. Phát biểu các định lí về mối quan hệ giữa cung nhỏ và dây căng cung đó trong một đường tròn.

Trả lời:

Với hai cung nhỏ của một đường tròn hay hai đường tròn bằng nhau thì:

- Hai cung bằng nhau căng hai dây bằng nhau.

- Hai dây bằng nhau căng hai cung bằng nhau.

- Cung lớn hơn căng dây lớn hơn.

- Dây lớn hơn căng cung lớn hơn.

7. Phát biểu định lí và hệ quả về các góc nội tiếp cùng chắn một cung.

Trả lời:

Định lí: Các góc nội tiếp cùng chắn một cung thì bằng nhau.

Hệ quả: Góc nội tiếp (nhỏ hơn hoặc bằng 90^o) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.

8. Phát biểu định lí về góc tạo bởi tia tiếp tuyến và dây cung.

Trả lời:

Định lí thuận: Góc tạo bởi tia tiếp tuyến và dây cung có số đo bằng nửa số đo của cung bị chắn.

Định lí đảo: Một góc có đỉnh nằm trên đường tròn, một cạnh chứa dây cung, có số đo bằng nửa số đo cung căng dây đó và cung này nằm bên trong góc thì cạnh kia là một tia tiếp tuyến.

9. Phát biểu quỹ tích cung chứa góc .

Trả lời:

Quỹ tích (tập hợp) các điểm nhìn một đoạn thẳng cho trước dưới một góc α không đổi là hai cung chứa góc α dựng trên đoạn thẳng đó (0^o < α < 180^o).

10. Phát biểu điều kiện để một tứ giác nội tiếp được đường tròn.

Trả lời:

Một tứ giác nội tiếp được đường tròn nếu thỏa mãn một trong các điều kiện sau:

+ Tổng của hai góc đối diện bằng 180^o.

+ Góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện.

+ Hai đỉnh kề cùng nhình cạnh nối hai đỉnh còn lại dưới góc bằng nhau.

+ Bốn đỉnh cách đều một điểm cố định.

11. Phát biểu một số dấu hiệu nhận biết tứ giác nội tiếp.

Trả lời:

Các dấu hiệu:

+ Tổng hai góc đối diện bằng 180^o.

+ Góc ngoài tại một đỉnh bằng góc trong ở đỉnh đối diện.

+ Bốn đỉnh cách đều một điểm cố định.

+ Hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc α

12. Phát biểu định lí về đường tròn ngoại tiếp và đường tròn nội tiếp của đa giác đều.

Trả lời:

Định lí: Mỗi đa giác đều có một và chỉ một đường tròn ngoại tiếp, có một và chỉ một đường tròn nội tiếp.

13. Nêu cách tính số đo cung nhỏ, cung lớn.

Trả lời:

Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó. Số đo của cung lớn bằng 360^o trừ đi số đo của cung nhỏ cùng căng dây cung.

14. Nêu cách tính số đo của góc nội tiếp theo số đo của cung bị chắn.

Trả lời:

Số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.

15. Nêu cách tính số đo của góc tạo bởi tia tiếp tuyến và dây cung theo số đo của cung bị chắn.

Trả lời:

Số đo cuả góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn.

16. Nêu cách tính số đo của góc có đỉnh ở bên trong đường tròn theo số đo của các cung bị chắn.

Trả lời:

Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo các cung bị chắn.

17. Nêu cách tính số đo của góc có đỉnh ở bên ngoài đường tròn theo số đo của các cung bị chắn.

Trả lời:

Số đo của góc có đỉnh bên ngoài đường tròn bằng nửa hiệu số đo của các cung bị chắn.

18. Nêu cách tính độ dài cung n^o của hình quạt tròn bán kính R.

Trả lời:

Độ dài l của cung n^o của hình quạt tròn bán kính R được tính theo công thức:

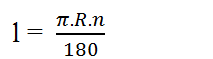
19. Nêu cách tính diện tích hình quạt tròn bán kính R, cung n^o.

Trả lời:

Diện tích S của hình quạt tròn bán kính R, cung n^o được tính theo công thức:

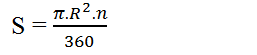
Tham khảo các lời giải Toán 9 Bài Ôn tập chương 3 khác:

• Mục lục Chương III: Góc Với Đường Tròn

• Câu hỏi ôn tập Chương 3 (câu 1 - 19 trang 100-101 SGK Toán 9 Tập 2): 1. Góc ở tâm là gì? 2. Góc nội tiếp là gì? ...

• Bài 88 (trang 103 SGK Toán 9 Tập 2): Hãy nêu tên mỗi góc trong các hình dưới đây: ...

• Bài 89 (trang 104 SGK Toán 9 Tập 2): Trong hình 67, cung AmB có số đo là 66^o. Hãy: ...

• Bài 90 (trang 104 SGK Toán 9 Tập 2): a) Vẽ hình vuông cạnh 4cm. ...

• Bài 91 (trang 104 SGK Toán 9 Tập 2): Trong hình 68, đường tròn tâm O có bán kính R = 2cm, ...

• Bài 92 (trang 104 SGK Toán 9 Tập 2): Hãy tính diện tích miền gạch sọc trong các hình 69, 70, 71 ...

• Bài 93 (trang 104-105 SGK Toán 9 Tập 2): Có ba bánh xe răng cưa A, B, C cùng chuyển độn ăn khớp với nhau. ...

• Bài 94 (trang 105 SGK Toán 9 Tập 2): Hãy xem biểu đồ hình quạt biểu diễn sự phân phối học sinh của một ...

• Bài 95 (trang 105 SGK Toán 9 Tập 2): Các đường cao hạ từ A và B của tam giác ABC cắt nhau tại H (góc C ...

• Bài 96 (trang 105 SGK Toán 9 Tập 2): Cho tam giác ABC nội tiếp đường tròn (O) và tia phân giác của góc A ...

• Bài 97 (trang 105 SGK Toán 9 Tập 2): Cho tam giác ABC vuông ở A. Trên AC lấy một điểm M và vẽ đường tròn ...

• Bài 98 (trang 105 SGK Toán 9 Tập 2): Cho đường tròn (O) và một điểm A cố định trên đường tròn. Tìm quỹ tích ...

• Bài 99 (trang 105 SGK Toán 9 Tập 2): Dựng ΔABC, biết BC = 6cm, góc BAC = 80^o, đường cao AH có độ dài là 2cm.

Tham khảo các lời giải Toán 9 Chương 3 khác:

• Ôn tập chương 3 (Câu hỏi - Bài tập)
• Tiếp theo: Toán 9 Tập 2 Chương 4
• Bài 1: Hình Trụ - Diện tích xung quanh và thể tích của hình trụ
• Bài 2: Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt - Luyện tập (trang 119-120)
• Bài 3: Hình cầu. Diện tích mặt cầu và thể tích hình cầu - Luyện tập (trang 126)
• Ôn tập chương 4 (Câu hỏi - Bài tập)

Xem thêm các loạt bài Để học tốt Toán lớp 9 hay khác:

• Giải sách bài tập Toán 9
• Chuyên đề Toán 9 (có đáp án - cực hay)
• Lý thuyết & 500 Bài tập Toán 9 (có đáp án)
• Các dạng bài tập Toán 9 cực hay
• Đề thi Toán 9
• Đề thi vào 10 môn Toán

• Hơn 20.000 câu trắc nghiệm Toán,Văn, Anh lớp 9 có đáp án

---

---

---