Các dạng bài Đồ thị hàm số (ôn thi vào lớp 10 Toán 2024)

Tài liệu Các dạng bài Đồ thị hàm số ôn thi vào lớp 10 Toán năm 2024 có lời giải chi tiết giúp học sinh củng cố kiến thức, ôn luyện để chuẩn bị tốt cho kì thi tuyển sinh vào lớp 10 môn Toán.

Các dạng bài Đồ thị hàm số (ôn thi vào lớp 10 Toán 2024)

Xem thử Đề ôn vào 10 Xem thử Đề vào 10 Hà Nội Xem thử Đề vào 10 TP.HCM Xem thử Đề vào 10 Đà Nẵng

Chỉ từ 150k mua trọn bộ Đề ôn thi vào 10 môn Toán năm 2024 bản word có lời giải chi tiết:

• B1: gửi phí vào tk: 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án

ĐỒ THỊ Y = AX + B (A ≠ 0), Y = AX² (A ≠ 0) VÀ TƯƠNG QUAN GIỮA CHÚNG

Dạng 1: Điểm thuộc đồ thị (đồ thị đi qua điểm)

Phương pháp

Để kiểm tra điểm M(x₀;y₀) có thuộc đồ thị hàm số không ta thay tọa độ của M        vào công thức hàm số. Nếu được đẳng thức đúng thì điểm M thuộc đồ thị hàm số , nếu được đẳng thức sai thì điểm M không thuộc đồ thị hàm số

Ví dụ

Ví dụ 1: Cho hàm số f(x) = 3x², hãy cho biết các điểm sau đây có thuộc đồ thị của hàm số không ?

a. M(-1;3)

b. N(2;4)

Giải

a. Thay tọa độ điểm M(-1;3) vào công thức của hàm số f(x) = 3x² ta được 

                    3 = 3.(-1)² ⇔3 = 3 (đúng)

          Vậy điểm M thuộc đồ thị của hàm số

b. Thay tọa độ điểm N(2;4) vào công thức của hàm số f(x) = 3x² ta được 

                    4 = 3.(2)² ⇔4 = 12 (sai)

          Vậy điểm N không thuộc đồ thị của hàm số

Ví dụ 2:Trong hệ trục toạ độ Oxy cho hàm số y = 2x + m. Tìm giá trị của m để đồ thị hàm số đi qua:

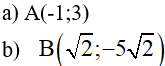
a) Để đồ thị hàm số y = 2x + m đi qua A(-1;3)

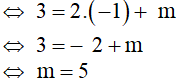
Vậy với m = 5 thì đồ thị hàm số y = 2x + m đi qua A(-1;3)

b)  Để đồ thị hàm số y = 2x + m đi qua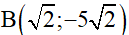

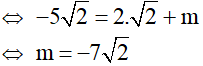
Vậy với 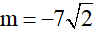thì đồ thị hàm y = 2x + m đi qua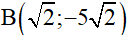

Dạng 2: Tìm giao điểm của hai đường y = f(x) và y = g(x)

Phương pháp 

 Để tìm giao điểm của hai đường y = f(x) và y = g(x) ta làm như sau 

• Lập phương trình hoành độ giao điểm : f(x) = g(x) (1)
• Số nghiệm của phương trình (1) là số giao điểm của hai đường y = f(x) và y = g(x)  
• Thay nghiệm x của phương trình (1) vào công thức y = f(x) hoặc y = g(x)  tìm y. Khi đó tọa độ giao điểm của hai đường y = f(x) và y = g(x) là (x;y)

Ví dụ 

Ví dụ 1: Cho (P) 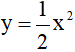 và đường thẳng y = 2x - 2. Tìm giao điểm của (P) và đường thẳng

Giải

    Phương trình hoành độ giao điểm:

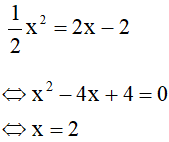
    Thay x = 2 vào phương trình đường thẳng y = 2x – 2 ta được y = 2

    Vậy (P) cắt đường thẳng tại một điểm A(2;2)

Ví dụ 2: Cho hai đường cong có phương trình là y = x² – 3x + 5 và y = x³ + x² + 2x + 5 . Tìm giao điểm của hai đường cong đó

Giải

    Phương trình hoành độ giao điểm: 

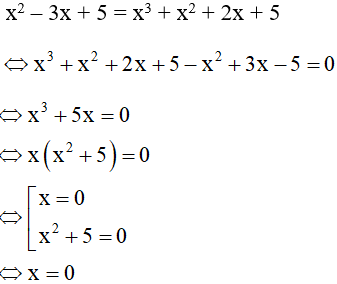
    Thay x = 0 vào phương trình đường cong y = x² – 3x + 5 ta được y = 5

    Vậy hai đường cong cắt nhau tại một điểm A(0;5)

Dạng 3: Tìm điều kiện để đường thẳng và parabol cắt nhau, tiếp xúc, không cắt nhau

Phương pháp

Cho (P) y = ax² (a ≠ 0) và đường thẳng y = kx + b 

Lập phương trình hoành độ giao điểm : ax² = kx + b⇔ ax² - kx – b = 0 (1)

    + Nếu phương trình (1) vô nghiệm thì parabol và đường thẳng không có điểm chung⇒ parabol và đường thẳng không cắt nhau

    + Nếu phương trình (1) có nghiệm kép thì parabol và đường thẳng có một điểm chung⇒ parabol và đường thẳng tiếp xúc nhau

    + Nếu phương trình (1) có hai nghiệm thì parabol và đường thẳng có hai điểm chung⇒ parabol và đường thẳng cắt nhau tại hai điểm phân biệt

Ví dụ: Xét sự tương giao giữa (P) y = 2x² với các đường sau đây

    a. Đường thẳng d₁: y = -3x + 5

    b. Đường thẳng d₂: y = -4x - 2

    c. Đường thẳng d₁: y = x - 15

Giải

a. Xét phương trình 

2x² = -3x + 5 

⇔2x² + 3x – 5 = 0 (1)

phương trình (1) là phương trình bậc hai có a + b + c = 2 + 3 – 5 = 0 nên có hai nghiệm phân biệt: x₁ = 1,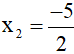

⇒(P) và d₁ cắt nhau tại hai điểm phân biệt

b. Xét phương trình 

2x² = -4x - 2

⇔ 2x² + 4x + 2 = 0

⇔ 2(x + 1)² = 0 

⇔x = -1

⇒(P) và d₂ tiếp xúc nhau

c. Xét phương trình 

2x² = x - 15

⇔ 2x² - x + 15 = 0 (1)

phương trình (1) là phương trình bậc hai có ∆ = (-1)² – 4.2.15 = -119 < 0 nên vô nghiệm 

⇒(P) và d₃ không cắt nhau 

Ví dụ 2: Trong mặt phẳng tọa độ Oxy cho đường thẳng (d): y = 3x + m² -1 và parabol (P): y = x²

a) Chứng minh (d) luôn cắt (P) tại hai điểm phân biệt với mọi m.

b) Gọi  là hoành độ các giao điểm của (d) và (P). Tìm m để (x₁ + 1)(x₂ + 1) = 1

Giải

a) Xét phương trình hoành độ giao điểm của (d) và (P)

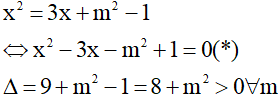
Suy ra phương trình (*) luôn có hai nghiệm phân biệt với mọi m hay (d)  luôn cắt (P) tại hai điểm phân biệt với mọi m

b) Ta có: 

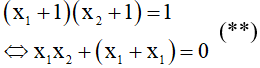
Áp dụng hệ thức Vi-et cho (*): 

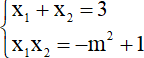
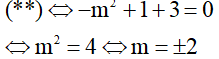
Vậy m = ±2.

Bài tập áp dụng

Bài 1: Cho hàm số 

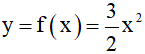
 1) Hãy tính 

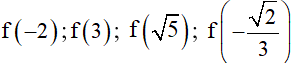
 2) Các điểm

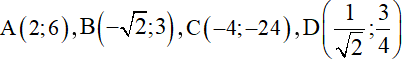
có thuộc đồ thị hàm số không ?

Bài 2: Đồ thị hàm số y = 7x – 10  có đi qua các điểm sau không?

          a. A(1;-3)

          b. B(0;5)

          c. C(3;0)

Bài 3: Trong hệ toạ độ Oxy, cho hàm số 

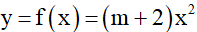
1) Tìm m để đồ thị hàm số đi qua các điểm :

   

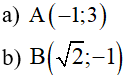
2) Thay m = 0. Tìm tọa độ giao điểm của đồ thị hàm số đã cho với đồ thị hàm số y = x + 1

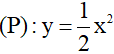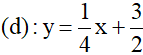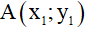Bài 4: Trong mặt phẳng với hệ tọa độ, cho parabol và đường thẳng . Gọi và 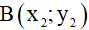lần lượt là các giao điểm của (P) với (d). Tính giá trị biểu thức .

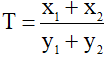Bài 5: Cho Parabol (P): y= x² và đường thẳng d: y = (2m-1)x - m + 2 (m là tham số) 

a) Chứng minh rằng với mọi m đường thẳng d luôn cắt (P) tại hai điểm phân biệt.

b) Tìm các giá trị của m để đường thẳng d luôn cắt (P) tại hai điểm phân biệt .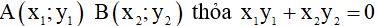

Bài 6: Cho parabol (P): y= x² và đường thẳng (d): y = -2ax - 4a(với a là tham số )

a) Tìm tọa độ giao điểm của (d) và (P) khi .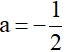

b) Tìm tất cả các giá trị của a để đường thẳng (d) cắt (P) tại hai điểm phân biệt có hoành độ 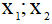thỏa mãn .

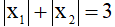Bài 7: Cho hai hàm số y= x² và,y = mx + 4 với m là tham số.

a) Khi m = 3, tìm tọa độ các giao điểm của hai đồ thị hàm số trên.

b) Chứng minh rằng với mọi giá trị m, đồ thị của hai hàm số đã cho luôn cắt nhau tại hai điểm phân biệt 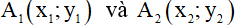.Tìm tất cả các giá trị của m sao cho .

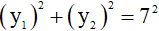Bài 8: Cho hàm số 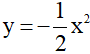 có đồ thị (P).

 Cho đường thẳng y = mx + n (Δ). Tìm m, n để đường thẳng (Δ) song song với đường thẳng y = -2x + 5 (d) và có duy nhất một điểm chung với đồ thị (P).

Bài 9: Trong mặt phẳng tọa độ Oxy cho đường thẳng (d): y = mx + 1 và parabol (P): y= x²

a) Chứng minh (d) luôn cắt (P)  tại hai điểm phân biệt với mọi m.

b) Gọi x₁, x₂ là hoành độ các giao điểm của (d) và (P). Tìm m để (x₁+2)(x₂+2) = 6  

Bài 10: Trong mặt phẳng tọa độ Oxy cho đường thẳng (d): y = x + m-1 và parabol (P): y= x² 

a) Tìm m để (d) đi qua điểm A(0;1)

b) Tìm m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt có hoành độ lần lượt là x₁; x₂ thỏa mãn: .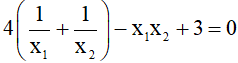

Bài 11: Trong mặt phẳng tọa độ Oxy cho Parabol (P): y= -x²  và đường thẳng (d): y = 3mx -3 (với m là tham số).

a) Tìm m để đường thẳng (d) đi qua điểm A(1;3)

b) Xác định các giá trị của m để (d) cắt (P) tại hai điểm phân biệt sao cho tổng 2 tung độ của hai giao điểm đó bằng -10

Bài 12: Cho parabol (P): y= x²  và đường thẳng (d) có phương trình: 

y = 2(m+1)x -3m+2

a) Tìm tọa độ giao điểm của (P) và (d) với m = 3.

b) Chứng minh (P) và (d) luôn cắt nhau tại 2 điểm phân biệt A và B với mọi m.

c) Gọi x₁; x₂ là hoành độ giao điểm của A và B.Tìm m để .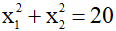

Bài 13: Cho parabol (P): y= x² và đường thẳng y = 2(m+1)x -2m+2 (m là tham số).

a) Với m = -5, tìm tọa độ giao điểm của parabol (P) và đường thẳng (d)

b) Chứng minh rằng: Với mọi m parabol (P)  và đường thẳng (d) cắt nhau tại hai điểm phân biệt. Tìm m sao cho hai giao điểm đó có hoành độ dương

Bài 14: Trong mặt phẳng tọa độ Oxy cho đường thẳng (d): y = mx -3 tham số m và Parabol (P): y= x²

a) Tìm m để đường thẳng (d) đi qua điểm A(1;0)

b) Tìm m để đường thẳng (d) cắt Parabol (P) tại hai điểm phân biệt có hoành độ lần lượt là x₁; x₂ thỏa mãn .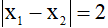

Bài 15: Tìm giao điểm của hai đồ thị hàm số sau

          a. y = 2x² – x + 1 và y = -x + 3

          b. y = 2x – 8 và y = 3x + 4

          c. y = -7x² và trục Ox

          d. y = x² – 7 và y = -5x² +x – 2

Bài 16: Cho parabol (P): y= x² và đường thẳng (d): y = x + 2a (a là tham số)

a) Tìm tọa độ giao điểm của (d) và (P) khi a = 1.

b) Tìm tất cả các giá trị của a để đường thẳng (d) cắt (P) tại hai điểm phân biệt có hoành độ x₁; x₂ thỏa mãn x₁.x₂ = 4.

Bài 17: Cho hai hàm số y = x² và y = -mx + 1, với m là tham số.

a) Khi m = 5, tìm tọa độ các giao điểm của hai đồ thị hàm số trên.

b) Chứng minh rằng với mọi giá trị m, đồ thị của hai hàm số đã cho luôn cắt nhau tại hai điểm phân biệt A₁(x₁; y₁) và A₂(x₂; y₂). Tìm tất cả các giá trị của m sao cho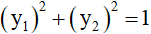

Bài 18: Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d): y = (2m + 5)x + 2m +6 (m là tham số) và parabol (P): y = x².

a) Khi m = 1 hãy xác định tọa độ giao điểm của đường thẳng (d) và parabol (P) bằng phương pháp đại số.

b) Tìm giá trị của m để đường thẳng (d) cắt parabol (P) tại  điểm phân biệt có hoành độ x₁, x₂ thỏa mãn: .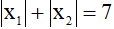

Bài 19: Cho hàm số y = ax² có đồ thị (P) và đường thẳng (d): y = mx + m -3

a) Tìm a để đồ thị (P) đi qua điểm B(2;-2).

Chứng minh rằng đường thẳng (d) luôn cắt đồ thị (P) tại hai điểm phân biệt C và D với mọi giá trị của m 

b) Gọi x_C và x_D lần lượt là hoành độ của hai điểm C và D. Tìm các giá trị của m sao cho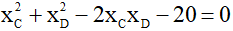

Bài 20

a) Cho hàm số 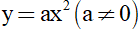có đồ thị parabol (P). Xác định a để (P) đi qua điểm .

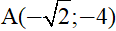b) Cho hàm số 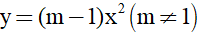có đồ thị là (P). Xác định m để (P) đi qua điểm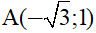

Xem thử Đề ôn vào 10 Xem thử Đề vào 10 Hà Nội Xem thử Đề vào 10 TP.HCM Xem thử Đề vào 10 Đà Nẵng

Xem thêm bộ tài liệu các dạng bài tập ôn thi vào lớp 10 môn Toán chọn lọc, hay khác:

• Các dạng bài Giải bất phương trình (ôn thi vào lớp 10 Toán 2024)
• Các dạng bài Phương trình chứa tham số (ôn thi vào lớp 10 Toán 2024)
• Các dạng toán Hệ thức Vi-et ôn thi vào lớp 10 năm 2024
• Các dạng bài Giải bài toán bằng cách lập phương trình ôn thi vào 10 năm 2024
• Các dạng toán thực tế ôn thi vào lớp 10 năm 2024

---