Các dạng bài Giải bài toán bằng cách lập phương trình (ôn thi vào 10 năm 2024)

Tài liệu Các dạng bài Giải bài toán bằng cách lập phương trình ôn thi vào 10 năm 2024 có lời giải chi tiết giúp học sinh củng cố kiến thức, ôn luyện để chuẩn bị tốt cho kì thi tuyển sinh vào lớp 10 môn Toán.

Các dạng bài Giải bài toán bằng cách lập phương trình (ôn thi vào 10 năm 2024)

Xem thử Đề ôn vào 10 Xem thử Đề vào 10 Hà Nội Xem thử Đề vào 10 TP.HCM Xem thử Đề vào 10 Đà Nẵng

Chỉ từ 150k mua trọn bộ Đề ôn thi vào 10 môn Toán năm 2024 bản word có lời giải chi tiết:

• B1: gửi phí vào tk: 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án

GIẢI BÀI TOÁN BẰNG CÁCH LẬP PHƯƠNG TRÌNH, HỆ PHƯƠNG TRÌNH THI VÀO 10

Dạng 1: Toán chuyển động

Phương pháp 

B1: Lập phương trình (hệ phương trình)

          - Chọn ẩn số và đặt điều kiện cho ẩn       

          - Biểu diễn các dữ kiện chưa biết qua ẩn số

          - Lập phương trình (hệ phương trình) biểu thị tương quan giữa ẩn số và các dữ kiện đã biết

B2: Giải phương trình (hệ phương trình)

B3: Đối chiếu nghiệm tìm được với điều kiện của ẩn số nếu có và đưa ra kết luận

Một số lưu ý:

          - quãng đường = vận tốc  × thời gian

          - vận tốc xuôi dòng = vận tốc khi nước yên lặng + vận tốc dòng nước

          - vận tốc ngược dòng = vận tốc khi nước yên lặng - vận tốc dòng nước

Ví dụ : 

Ví dụ 1: Một ô tô đi từ A đến B trong một thời gian nhất định. Nếu xe chạy với vận tốc 35km/h thì đến chậm mất 2 giờ. Nếu xe chạy với vận tốc 50km/h thì đến sớm hơn 1 giờ. Tính quãng đường AB và thời gian dự định lúc đầu

Giải

Gọi t là thời gian dự định lúc đầu ( t đơn vị là giờ, t > 1)

Nếu xe chạy với vận tốc 35km/h thì thời gian đi từ A đến B là: t + 2 (giờ)

 quãng đường AB là: 35.(t + 2) km  (1)

Nếu xe chạy với vận tốc 50km/h thì thời gian đi tử A đến B là: t - 1 (giờ)

 quãng đường AB là: 50.(t - 1) km (2)

Từ (1) và (2) ta có phương trình:   

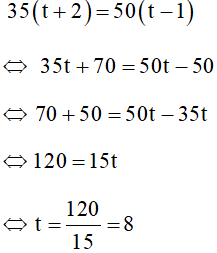
   (thỏa mãn điều kiện)

Vậy thời gian dự định ban đầu là 8(giờ) và quãng đường AB dài 35.(t + 2) = 35.10 = 350 (km)

Ví dụ 2: Lúc 6 giờ một ô tô chạy từ A về B. Sau đó nửa giờ, một xe máy chạy từ B về A. Ô tô gặp xe máy lúc 8 giờ. Biết vận tốc ô tô lớn hơn vận tốc xe máy là 10km/h và khoảng cách AB = 195km. Tính vận tốc mỗi xe.

Giải

Gọi vận tốc ô tô là  x (km/h) (x>0).

Gọi vận tốc xe máy là  y (km/h) (y>0).

Vì vận tốc ô tô hơn vận tốc xe máy là 10km/h nên ta có phương trình: x – y = 10 

Thời gian ô tô đã đi cho đến lúc gặp xe máy là: 8 – 6 = 2(giờ).

Thời gian xe máy đã đi cho đến lúc gặp ô tô là:   

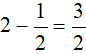(giờ).

Quãng đường ô tô chạy trong 2 giờ là 2x(km).

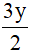Quãng đường xe máy chạy trong giờ là  (km).

Vì quãng đường AB dài 195km nên ta có phương trình 

   .

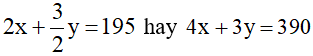Do đó ta có hệ hai phương trình :

 

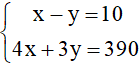
Giải hệ này ta được  x = 60; y = 50 (thỏa mãn điều kiện).

Vậy vận tốc ô tô là 60 km/h, vận tốc xe máy là 50 km/h.

Dạng 2: Toán công việc (làm chung, làm riêng, năng suất...)

Phương pháp 

B1: Lập phương trình (hệ phương trình)

          - Chọn ẩn số và đặt điều kiện cho ẩn

          - Biểu diễn các dữ kiện chưa biết qua ẩn số

          - Lập phương trình (hệ phương trình) biểu thị tương quan giữa ẩn số và các dữ kiện đã biết

B2: Giải phương trình (hệ phương trình)

B3: Đối chiếu nghiệm tìm được với điều kiện của ẩn số nếu có và đưa ra kết luận

 Lưu ý: Khối lượng công việc = Năng suất × Thời gian

Ví dụ 1: Một hợp tác xã dự kiến thu hoạch 200ha lúa trong thời gian đã định. Song thực tế mỗi ngày thu hoạch nhanh hơn so với kế hoạch là 5ha nên đã hoàn thành công việc nhanh hơn dự kiến 2 ngày. Hỏi theo dự kiến mỗi ngày thu hoạch bao nhiêu ha ? (mỗi ngày thu hoạch được số lúa là như nhau)

Giải

Gọi t là số ngày hợp tác xã dự kiến thu hoạch xong 200ha lúa (t > 2)

  ⇒theo dự kiến một ngày hợp tác xã thu hoạch được số ha lúa l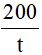à   (ha)

Thực tế, mỗi ngày hợp tác thu hoạch được l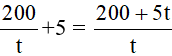à (ha)

Do đó số ngày hoàn thành công việc là: 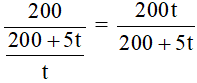 (ngày)

Vì công việc hoàn thành sớm hơn dự kiến 2 ngày nên ta có phương trình

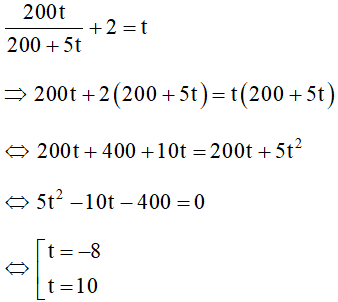
Với t = -8 không thỏa mãn điều kiện (loại)

Với t = 10 thỏa mãn điều kiện (nhận)

Vậy theo dự kiến mỗi ngày hợp tác thu hoạch số ha lúa l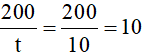à   (ha)

Ví dụ 2: Hai người cùng làm chung một công việc trong 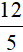 giờ thì xong. Nếu mỗi người làm một mình thì người thứ nhất hoàn thành xong công việc ít hơn người thứ hai là 2 giờ. Hỏi nếu mỗi người làm một mình thì làm trong bao lâu để xong công việc( biết rằng mỗi giờ người thứ nhất làm được khối lượng công việc là như nhau và mỗi giờ người thứ hai làm được khối lượng công việc là như nhau)

Giải

Gọi thời gian người thứ nhất làm một mình xong công việc là x (giờ), x > 0

Thời gian người thứ hai làm một mình xong công việc là x + 2 (giờ)

Trong 1 giờ người thứ nhất làm được  công việc

Trong 1 giờ người thứ hai làm được 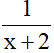 công việc

Trong 1 giờ cả hai người làm được 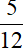 công việc nên ta có phương trình

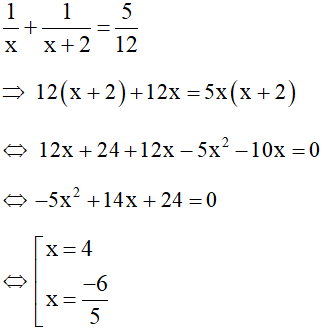
Với 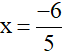  < 0 (loại)

Với x = 4 (thỏa mãn điều kiện)

Vậy người thứ nhất làm một mình xong công việc trong 4 giờ, người thứ hai làm một mình xong công việc trong 6 giờ

Dạng 3: Các bài toán tìm số

Phương pháp 

B1: Lập phương trình (hệ phương trình)

          - Chọn ẩn số và đặt điều kiện cho ẩn

          - Biểu diễn các dữ kiện chưa biết qua ẩn số

          - Lập phương trình (hệ phương trình) biểu thị tương quan giữa ẩn số và các dữ kiện đã biết

B2: Giải phương trình (hệ phương trình)

B3: Đối chiếu nghiệm tìm được với điều kiện của ẩn số nếu có và đưa ra kết luận

Lưu ý: 

Số có hai chữ số được ký hiệu là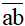

Giá trị của số: 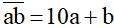 ; (Đk: 1 ≤ a ≤ 9 và 0 ≤ b ≤ 9, a,b ∈N)

Số có ba chữ số được ký hiệu là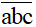  

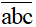 = 100a +10b + c, (Đk: 1 ≤ a ≤ 9 và 0 ≤ b, c ≤ 9; a, b, c ∈ N)

Tổng hai số x; y là: x + y

 Tổng bình phương hai số x, y là: x² + y²

Bình phương của tổng hai số x, y là: (x + y)²

Tổng nghịch đảo hai số x, y là :   .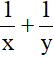

Ví dụ : 

Ví dụ 1: Tìm tất cả các số tự nhiên có hai chữ số biết rằng tổng các chữ số của nó bằng 5 và tổng các bình phương hai chữ số của nó bằng 13

Giải

Gọi chữ số hàng chục của số tự nhiên có hai chữ số là x (0 < x ≤ 5)

 ⇒ chữ số hàng đơn vị là 5 – x 

Vì tổng các bình phương hai chữ số của nó bằng 13 nên ta có phương trình

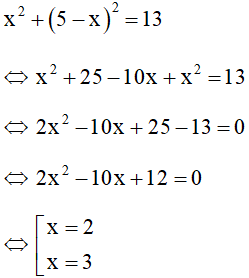
Với x = 2 thì chữ số hàng chục bằng 2 và chữ số hàng đơn vị bằng 3. Do đó số phải tìm là 23

Với x = 3 thì chữ số hàng chục bằng 3 và chữ số hàng đơn vị bằng 2. Do đó số phải tìm là 32

Vậy có 2 số tự nhiên thỏa mãn đề bài là 23 và 32

Ví dụ 2: Cho số tự nhiên có hai chữ số, tổng của chữ số hàng chục và chữ số hàng đơn vị bằng 14. Nếu đổi chữ số hàng chục và chữ số hàng đơn vị cho nhau thì được số mới lớn hơn số đã cho 18 đơn vị. Tìm số đã cho.

Giải

Gọi chữ số hàng chục của số cần tìm là x, điều kiện x ∈ N, (0 < x ≤ 9)

Gọi chữ số hàng đơn vị của số cần tìm là y, điều kiện y ∈ N, (0 ≤ y ≤ 9)

Tổng chữ số hàng chục và chữ số hàng đơn vị bằng 14 nên có phương trình:        x + y = 14

Số đó là: 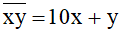. Nếu đổi chữ số hàng chục và chữ số hàng đơn vị cho nhau thì số mới là: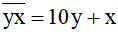

Theo bài ra ta số mới lớn hơn số đã cho 18 đơn vị nên có phương trình:   

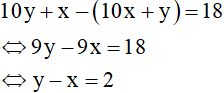
Từ đó ta có hệ phương trình 

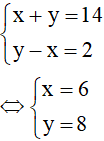
(thoả mãn điều kiện)

Số cần tìm là 68.

Dạng 4: Các bài toán liên quan đến chảy chung, chảy riêng của vòi nước

Phương pháp 

B1: Lập phương trình (hệ phương trình)

          - Chọn ẩn số và đặt điều kiện cho ẩn

          - Biểu diễn các dữ kiện chưa biết qua ẩn số

          - Lập phương trình (hệ phương trình) biểu thị tương quan giữa ẩn số và các dữ kiện đã biết

B2: Giải phương trình (hệ phương trình)

B3: Đối chiếu nghiệm tìm được với điều kiện của ẩn số nếu có và đưa ra kết luận

Chú ý: Lượng nước chảy vào bể tỉ lệ thuận với thời gian

           Nếu vòi nào chảy riêng một mình đầy bể trong x (giờ) thì trong 1 giờ vòi đó chảy được  (bể).

Ví dụ 1:Hai vòi nước cùng chảy đầy một bể không có nước trong 3h 45ph . Nếu chảy riêng rẽ, mỗi vòi phải chảy trong bao lâu mới đầy bể ? biết rằng vòi chảy sau lâu hơn vòi trước 4 h .

Giải

Gọi thời gian vòi đầu chảy một mình đầy bể là x ( x > 0 , x tính bằng giờ )

Gọi thời gian vòi sau chảy một mình đầy bể là  y ( y > 4 , y tính bằng giờ )

1 giờ vòi đầu chảy được   ( bể )

1 giờ vòi sau chảy được 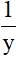  ( bể )

1 giờ hai vòi  chảy được 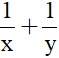   ( bể )             (1)

Hai vòi cùng chảy thì đầy bể trong 3h 45p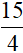h =  h

Vậy 1 giờ cả hai vòi chảy được 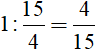  ( bể )  ( 2)

Từ (1) và (2) ta có hệ phương trình  

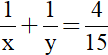
Mặt khác ta biết nếu chảy một mình thì vòi sau chảy lâu hơn vòi trước 4 giờ tức là y – x = 4

Vậy ta có hệ phương trình   

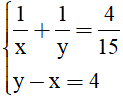
Ta có  

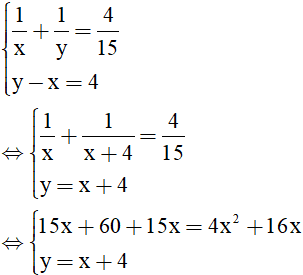
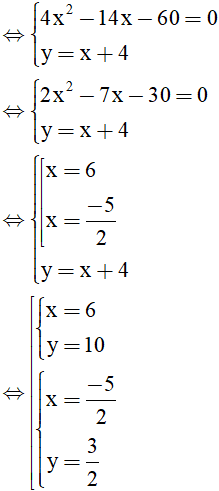
Ta thấy x = 6, y = 10 thoả mãn đk của ẩn 

Trường hợp 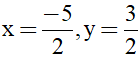   loại vì x < 0

Vậy Vòi đầu chảy một mình đầy bể trong 6 h 

        Vòi sau chảy một mình đầy bể trong 10 h 

Ví dụ 2: Hai vòi nước cùng chảy vào một cái bể không có nước thì trong 5 giờ sẽ đầy bể. Nếu vòi thứ nhất chảy trong 3 giờ và vòi thứ 2 chảy trong 4 giờ thì được 2/3 bể nước. Hỏi nếu mỗi vòi chảy một mình thì trong bao lâu mới đầy bể.

Giải 

Gọi thời gian vòi thứ nhất chảy một mình đầy bể là x (giờ), thời gian vòi thứ hai chảy một mình đầy bể là y (giờ). (Điều kiện: x, y > 5 )

Trong 1 giờ vòi thứ nhất chảy được 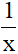  bể; vòi thứ hai chảy được  bể

Trong 1 giờ cả hai vòi chảy được 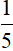 bể.

Vì hai vòi nước cùng chảy vào bể không có nước thì trong 5 giờ sẽ đầy bể nên ta có phương trình:              

           

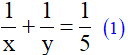
Nếu vòi thứ nhất chảy trong 3 giờ và vòi thứ 2 chảy trong 4 giờ thì được  bể nên ta có phương trình:        

           

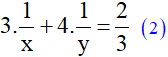
Từ (1) và (2) ta có hệ phương trình:  

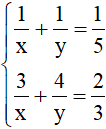
Giải  hệ phương trình trên ta đươc x = 7,5  ; y = 15(thỏa mãn điều kiện) 

Vậy thời gian vòi thứ nhất chảy một mình đầy bể là  7,5 giờ; thời gian vòi thứ hai chảy một mình đầy bể là 15 giờ.

Dạng 5: Các bài toán liên quan đến tỉ số phần trăm

Phương pháp 

B1: Lập phương trình (hệ phương trình)

          - Chọn ẩn số và đặt điều kiện cho ẩn

          - Biểu diễn các dữ kiện chưa biết qua ẩn số

          - Lập phương trình (hệ phương trình) biểu thị tương quan giữa ẩn số và các dữ kiện đã biết

B2: Giải phương trình (hệ phương trình)

B3: Đối chiếu nghiệm tìm được với điều kiện của ẩn số nếu có và đưa ra kết luận

Ví dụ: Trong tháng giêng hai tổ sản xuất được 720 chi tiết máy. Trong tháng hai, tổ I vượt mức 15%, tổ II vượt mức 12% nên sản xuất được 819 chi tiết máy. Tính xem trong tháng giêng mỗi tổ sản xuất được bao nhiêu chi tiết máy ?

Giải

Gọi x là số chi tiết máy tổ I làm được trong tháng giêng ( x > 0,  )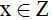

Gọi y là số chi tiết máy tổ II làm được trong tháng giêng ( y > 0,  )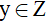

Trong tháng giêng hai tổ sản xuất được 720 chi tiết máy nên ta có phương trình 

                                                   x + y = 720 (1)

Trong tháng hai, tổ I vượt mức 15% nên sản xuất được 1,15x ( chi tiết)

Trong tháng hai, tổ II vượt mức 12% nên sản xuất được 1,12y ( chi tiết)

Vì tháng hai cả hai tổ sản xuất được 819 chi tiết nên ta có phương trình

                                               1,15x + 1,12y = 819 (2)

Từ (1) và (2) ta có hệ  

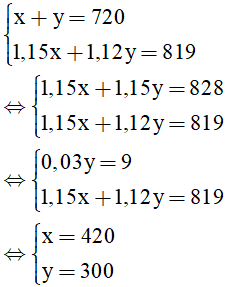
  (thỏa mãn)

Vậy tháng giêng tổ I sản xuất được 420 chi tiết, tổ II sản xuất được 300 chi tiết

Dạng 6: Các bài toán liên quan đến Lý – Hóa

Phương pháp 

B1: Lập phương trình (hệ phương trình)

          - Chọn ẩn số và đặt điều kiện cho ẩn

          - Biểu diễn các dữ kiện chưa biết qua ẩn số

          - Lập phương trình (hệ phương trình) biểu thị tương quan giữa ẩn số và các dữ kiện đã biết

B2: Giải phương trình (hệ phương trình)

B3: Đối chiếu nghiệm tìm được với điều kiện của ẩn số nếu có và đưa ra kết luận

Một số lưu ý:

-Công thức: 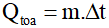 (Qtỏa là nhiệt lượng tỏa ra, đơn vị là Kcal; m là khối lượng khối lượng chất lỏng, đơn vị là kg; ∆t = nhiệt độ ban đầu – nhiệt độ sau khi pha)

-Công thức: 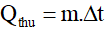 (Qthu là nhiệt lượng thu vào, đơn vị là Kcal; m là khối lượng khối lượng chất lỏng, đơn vị là kg; ∆t = nhiệt độ sau khi pha - nhiệt độ ban đầu )

-

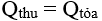
- Công thức 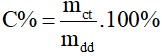 ( C% là nồng độ phần trăm, mct là khối lượng chất tan, mdd là khối lượng dung dịch)

- Công thức m = D.V( m là khối lượng chất lỏng, D là khối lượng riêng của chất lỏng, V là thể tích)

Ví dụ 1: Pha 2 lít nước sôi (1000C) và 3 lít nước lạnh (200C) thì được hỗn hợp nước có nhiệt độ bao nhiêu?

Giải

1 lít nước = 1kg nước

Gọi nhiệt độ của hỗn hợp nước là x⁰C (20 < x < 100)

Nhiệt lượng tỏa ra của nước là: Q_tỏa = 2(100 – x)

Nhiệt lượng thu vào của nước là: Q_thu = 3(x - 20)

Vì Q_thu = Q_tỏa nên ta có phương trình: 2(100 – x) = 3(x - 20)

   

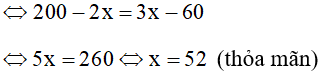
Vậy nhiệt độ của hỗn hợp nước là 52⁰C

Ví dụ 2: Khi thêm 200g axit vào dung dịch A được dung dịch B có nồng độ axit là 50%. Lại thêm 300g nước vào dung dịch B được dung dịch C có nồng độ axit là 40%. Tính nồng độ axit trong dung dịch A

Giải

Gọi khối lượng axit và nước trong dung dịch A lần lượt là x(g) và y(g)

Điều kiện: x > 0, y > 0

Trong dung dịch B khối lượng chất tan là x + 200, khối lượng dung dịch là x + y + 200

Nồng độ axit trong dung dịch B là 50% nên ta có phương trình

   

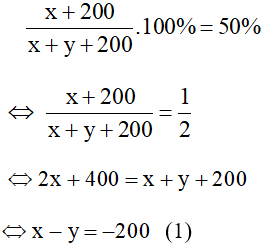
Trong dung dịch C khối lượng chất tan là x + 200, khối lượng dung dịch là x + y + 200 +300 = x + y +500

Nồng độ axit trong dung dịch C là 40% nên ta có phương trình

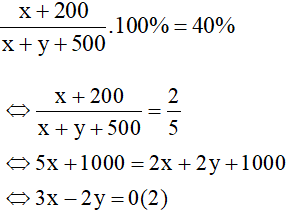
Từ (1) và (2) ta có hệ phương trình  

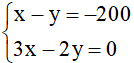
Giải hệ ta được x = 400, y = 600 (thỏa mãn)

Vậy nồng độ axit trong dung dịch A là: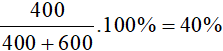  

Dạng 7: Các bài toán liên quan đến hình học

Phương pháp 

B1: Lập phương trình (hệ phương trình)

          - Chọn ẩn số và đặt điều kiện cho ẩn

          - Biểu diễn các dữ kiện chưa biết qua ẩn số

          - Lập phương trình (hệ phương trình) biểu thị tương quan giữa ẩn số và các dữ kiện đã biết

B2: Giải phương trình (hệ phương trình)

B3: Đối chiếu nghiệm tìm được với điều kiện của ẩn số nếu có và đưa ra kết luận

Một số lưu ý:

          - Nếu hình chữ nhật có 2 cạnh là a và b thì diện tích của hình chữ nhật là a.b,

          chu vi của hình chữ nhật là 2(a + b)

          - Nếu hình vuông có cạnh bằng a thì diện tích hình vuông là a2, chu vi của hình vuông là 4a

          - Chu vi tam giác bằng tổng độ dài 3 cạnh, diện tích tam giác bằng một nửa tích độ dài đường cao nhân cạnh đáy tương ứng

          - Nếu tam giác vuông có 2 cạnh góc vuông là a và b, cạnh huyền là c thì 

                                                     c² = a² + b² (Định lý Pi-ta-go)

Ví dụ 1: Một hình chữ nhật có chiều dài gấp 3 lần chiều rộng. Nếu cả chiều dài và chiều rộng cùng tăng thêm 5cm thì được một hình chữ nhật mới có diện tích bằng 153cm². Tính chu vi của hình chữ nhật ban đầu

Giải

Gọi chiều rộng của hình chữ nhật là x cm (x > 0)

 ⇒chiều dài của hình chữ nhật là 3x (cm)

Chiều rộng tăng thêm 5cm thì có độ dài mới là x + 5 (cm)

Chiều dài tăng thêm 5cm thì có độ dài mới là 3x + 5 (cm)

Vì diện tích hình chữ nhật mới là 153cm² nên ta có phương trình

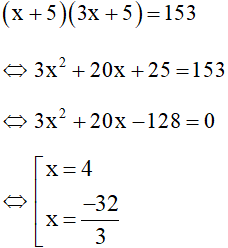
Với x = 4 thỏa mãn x > 0 (nhận)

Với 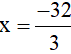 không thỏa mãn x > 0 (loại)

Vậy hình chữ nhật ban đầu có chiều rộng là 4cm, chiều dài là 12cm. Do đó chu vi của hình chữ nhật ban đầu là: 2(4 + 12) = 32 (cm)

Ví dụ 2 : Một mảnh vườn hình chữ nhật có chu vi 34m. Nếu tăng thêm chiều dài 3m và chiều rộng 2m thì diện tích tăng thêm 45m². Hãy tính chiều dài, chiều rộng của mảnh vườn.

Giải 

Gọi chiều dài, chiều rộng của mảnh vườn hình chữ nhật lần lượt là x(m); y(m). Điều kiện: x > y > 0(*)

Chu vi của mảnh vườn là : 2(x + y) = 34  (m).     (1)

Diện tích trước khi tăng:  xy (m²).

Diện tích sau khi tăng: (x + 3)(y + 2) (m²).

Sau khi tăng chiều dài và chiều rộng thì diện tích tăng thêm 45m2 nên ta có phương trình : (x + 3)(y + 2) – xy = 45   (2)

Từ (1) và (2) ta có hệ: 

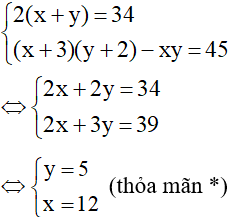
Vậy chiều dài là 12m, chiều rộng là 5m.

 Bài tập áp dụng

Bài 1: Tìm hai số tự nhiên biết số lớn hơn số bé 3 đơn vị và tổng các bình phương của chúng bằng 369

Bài 2: Một phân số có tử số bé hơn mẫu số là 11. Nếu bớt tử số đi 7 đơn vị và tăng mẫu lên 4 đơn vị thì sẽ được phân số nghịch đảo của phân số đã cho. Tìm phân số đó

Bài 3: Tìm hai số biết tổng của hai số bằng 51 và 2/3 số thứ nhất bằng 1/6 số thứ hai

Bài 4: Tìm hai số chẵn nguyên dương liên tiếp biết tổng bình phương của hai số là 244

Bài 5: Một người đi xe máy từ A đến B vận tốc 25km/h. Lúc về người đó đi với vận tốc 30km/h nên thời gian về ít hơn thời gian đi là 20 phút. Tính quãng đường AB

Bài 6: Lúc 6 giờ sáng một ô tô xuất phát từ A đến B với vận tốc 40km/h. Khi đến B người đó làm nhiệm vụ giao nhận hàng trong 30 phút rồi cho xe quay về A với vận tốc 30km/h. Tính quãng đường AB biết ô tô về đến A lúc 10 giờ sáng cùng ngày 

Bài 7: Hai xe máy khởi hành lúc 7 giờ sáng từ A đến B. Xe thứ nhất chạy với vận tốc 30km/h, xe thứ hai chạy với vận tốc lớn hơn xe thứ nhất 6km/h. Trên đường đi xe thứ hai dừng lại nghỉ 40 phút rồi lại tiếp tục chạy với vận tốc cũ. Tính quãng đường AB biết hai xe về đến B cùng một lúc 

Bài 8: Hai người đi xe đạp cùng lúc, ngược chiều nhau từ hai địa điểm A và B cách nhau 42km và gặp nhau sau 2 giờ. Tính vận tốc của mỗi người biết rằng người đi từ A mỗi giờ đi nhanh hơn người đi từ B là 3km

Bài 9: Hai đội công nhân làm một đoạn đường. Đội 1 làm xong một nửa đoạn đường thì đội 2 đến làm tiếp nửa còn lại với thời gian dài hơn thời gian đội 1 đã làm là 30 ngày. Nếu hai đội cùng làm thì trong 72 ngày xong cả đoạn đường .Hỏi mỗi đội đã làm bao nhiêu ngày trên đoạn đường này? ( biết rằng mỗi ngày khối lượng công việc mà đội 1 làm được là như nhau và mỗi ngày khối lượng công việc mà đội 2 làm được là như nhau)

Bài 10: Hai đội công nhân trồng rừng phải hoàn thành kế hoạch trong cùng một thời gian. Đội 1 phải trồng 40 ha, đội 2 phải trồng 90 ha. Đội 1 hoàn thành công việc sớm hơn 2 ngày so với kế hoạch. Đội 2 hoàn thành muộn hơn 2 ngày so với kế hoạch. Nếu đội 1 làm công việc trong một thời gian bằng thời gian đội 2 đã làm và đội 2 làm trong thời gian bằng đội 1 đã làm thì diện tích trồng được của hai đội bằng nhau. Tính thời gian mỗi đội phải làm theo kế hoạch? ( biết rằng mỗi ngày diện tích rừng mà đội 1 trồng được là như nhau và mỗi ngày diện tích rừng mà đội 2 trồng được là như nhau)

Bài 11: Hai đội công nhân cùng làm chung một công việc. Thời gian để đội I làm một mình xong công việc ít hơn thời gian để đội II làm một mình xong công việc đó là 4 giờ. Tổng thời gian này gấp 4,5 lần thời gian hai đội cùng làm chung để xong công việc đó. Hỏi mỗi đội làm một mình thì phải bao lâu mới xong? ( biết rằng mỗi giờ khối lượng công việc mà đội 1 làm được là như nhau và mỗi giờ khối lượng công việc mà đội 2 làm được là như nhau)

Bài 12: Một xí nghiệp giao cho một công nhân làm 120 sản phẩm trong thời gian quy định. Sau khi làm được 2 giờ, người đó cải tiến kĩ thuật nên đã tăng được 4 sản phẩm mỗi giờ so với dự kiến. Vì vậy trong thời gian quy định không những hoàn thành kế hoạch trước 1 giờ mà còn vượt mức 16 sản phẩm. Tính năng suất làm lúc đầu (biết rằng mỗi giờ xí nghiệp làm được số sản phẩm là như nhau)

Bài 13: Một thửa ruộng tam giác có diện tích 180m2. Tính chiều dài cạnh đáy thửa ruộng, biết rằng nếu tăng cạnh đáy lên 4m và chiều cao tương ứng giảm đi 1m thì diện tích không đổi  

Bài 14: Một mảnh đất hình chữ nhật có chiều dài hơn chiều rộng 6m và bình phương đường chéo gấp 5 lần chu vi. Tính chiều dài và chiều rộng của hình chữ nhật       

Bài 15: Một tam giác vuông có 2 cạnh góc vuông hơn kém nhau 8m. Nếu tăng một cạnh góc vuông lên 2 lần và giảm một cạnh góc vuông đi 3 lần thì được tam giác mới có diện tích 51m². Tính độ dài hai cạnh góc vuông  

Bài 16: Một hình chữ nhật có chiều rộng ngắn hơn chiều dài 1m. Nếu chiều dài tăng thêm 1/4 lần độ dài của nó thì được một hình chữ nhật mới có diện tích tăng thêm 3m². Tính diện tích của hình chữ nhật ban đầu

Bài 17: Hai người thợ cùng làm chung một công việc trong 7 giờ 12 phút thì xong. Nếu người thứ nhất làm trong 5 giờ và người thứ hai làm trong 6 giờ thì cả hai người chỉ làm được 3/4 công việc. Hỏi mỗi người làm công việc đó trong mấy giờ thì xong?

Bài 18:Nếu vòi A chảy 2 giờ và vòi B chảy trong 3 giờ thì được 4/5 hồ. Nếu vòi A chảy trong 3 giờ và vòi B chảy trong 1 giờ 30 phút thì được 1/2 hồ. Hỏi nếu chảy một mình mỗi vòi chảy trong bao lâu mới đầy hồ.

Bài 19: Hai vòi nước cùng chảy vào một bể thì sau 6 giờ đầy bể. Nếu mỗi vòi chảy một mình cho đầy bể thì vòi II cần nhiều thời gian hơn vòi I là 5 giờ. Tính thời gian mỗi vòi chảy một mình đầy bể?

Bài 20 : Năm ngoái tổng số dân của hai tỉnh A và B là 4 triệu người. Dân số tỉnh A năm nay tăng 1,2%, còn tỉnh B tăng 1,1%. Tổng số dân của cả hai tỉnh năm nay là 4 045 000 người. Tính số dân của mỗi tỉnh năm ngoái và năm nay?

Bài 21: Một khu vườn hình chữ nhật có chu vi là 280 m. Người ta làm lối đi xung quanh vườn (thuộc đất trong vườn) rộng 2 m. Tính kích thước của vườn, biết rằng đất còn lại trong vườn để trồng trọt là 4256 m².

Bài 22: Cho một hình chữ nhật. Nếu tăng chiều dài lên 10 m, tăng chiều rộng lên 5 m thì diện tích tăng 500 m². Nếu giảm chiều dài 15 m và giảm chiều rộng 9 m thì diện tích giảm 600 m². Tính chiều dài, chiều rộng ban đầu.

Bài 23:Cho một tam giác vuông. Nếu tăng các cạnh góc vuông lên 2 cm và 3 cm thì diện tích tam giác tăng 50 cm². Nếu giảm cả hai cạnh đi 2 cm thì diện tích sẽ giảm đi 32 cm². Tính hai cạnh góc vuông..

Bài 24: Nếu tử số của một phân số được tăng gấp đôi và mẫu số thêm 8 thì giá trị của phân số bằng 1/4 . Nếu tử số thêm 7 và mẫu số tăng gấp 3 thì giá trị phân số bằng 5/24 . Tìm phân số đó.

Bài 25:Nếu thêm 4 vào tử và mẫu của một phân số thì giá trị của phân số giảm 1. Nếu bớt 1 vào cả tử và mẫu, phân số tăng 3/2 . Tìm phân số đó.

Bài 26: Hai tổ sản xuất phải hoàn thành 90 sản phẩm. Tổ I vượt mức 15% kế hoạch của tổ. Tổ II vượt mức 12% kế hoạch của tổ. Do đó, cả hai tổ làm được 102 sản phẩm. Hỏi theo kế hoạch mỗi tổ phải làm bao nhiêu sản phẩm.

Bài 27: Theo kế hoạch hai tổ sản xuất 1000 sản phẩm trong một thời gian dự định. Do áp dụng kỹ thuật mới nên tổ I vượt mức kế hoạch 15% và tổ hai vượt mức 17%. Vì vậy trong thời gian quy định cả hai tổ đã sản xuất được tất cả được 1162 sản phẩm. Hỏi số sản phẩm của mỗi tổ là bao nhiêu?

Bài 28: Pha 3 lít nước nóng với 2 lít nước lạnh ở 200C để được nước có nhiệt độ 620C. Tính nhiệt độ của nước nóng

Bài 29: Có hai loại quặng chứa 75% sắt và 50% sắt. Tính khối lượng của mỗi loại quặng đem trộn để được 25 tấn quặng sắt chứa 66% sắt

Bài 30: Người ta hòa lẫn 4kg chất lỏng I với 3kg chất lỏng II thì được hỗn hợp có khối lượng riêng là 700kg/m³. Biết khối lượng riêng của chất lỏng I lớn hơn khối lượng riêng của chất lỏng II là 200kg/m³. Tính khối lượng riêng của mỗi chất lỏng

Xem thử Đề ôn vào 10 Xem thử Đề vào 10 Hà Nội Xem thử Đề vào 10 TP.HCM Xem thử Đề vào 10 Đà Nẵng

Xem thêm bộ tài liệu các dạng bài tập ôn thi vào lớp 10 môn Toán chọn lọc, hay khác:

• Các dạng toán Hệ thức Vi-et ôn thi vào lớp 10 năm 2024
• Các dạng toán thực tế ôn thi vào lớp 10 năm 2024
• Các dạng toán Hình học ôn thi vào lớp 10 năm 2024
• Các dạng Toán nâng cao ôn thi vào lớp 10 năm 2024
• Cấu trúc đề thi vào lớp 10 môn Toán năm 2024

---