Các dạng toán Hình học ôn thi vào lớp 10 năm 2025
Tài liệu Các dạng toán Hình học ôn thi vào lớp 10 năm 2025 có lời giải chi tiết giúp học sinh củng cố kiến thức, ôn luyện để chuẩn bị tốt cho kì thi tuyển sinh vào lớp 10 môn Toán.
Các dạng toán Hình học ôn thi vào lớp 10 năm 2025
Xem thử Đề ôn vào 10 Xem thử Đề vào 10 Hà Nội Xem thử Đề vào 10 TP.HCM Xem thử Đề vào 10 Đà Nẵng
Chỉ từ 100k mua trọn bộ Đề ôn thi vào 10 môn Toán năm 2025 bản word có lời giải chi tiết:
- B1: gửi phí vào tk:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án
CÁC DẠNG TOÁN HÌNH ÔN THI VÀO 10
Dạng 1: Chứng minh các điểm thuộc đường tròn
Phương pháp
Cách 1: Chứng minh các điểm đó cùng cách đều một điểm O cố định. Khi đó các điểm đã cho cùng thuộc đường tròn tâm O
Cách 2: Sử dụng tứ giác nội tiếp. Chẳng hạn để chứng minh 5 điểm A, B, C, D, E cùng thuộc một đường tròn ta chứng minh ABCD, ABCE là tứ giác nội tiếp
Ví dụ 1: Cho hình thoi ABCD có góc A bằng 600 , AB = a. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh rằng 6 điểm E, F, G, H, B, D cùng nằm trên một đường tròn. Xác định tâm và tính bán kính của đường tròn đó theo a.
Giải
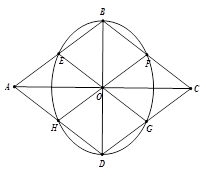
Gọi O là giao điểm của AC và BD ta có OB = OD
Do ABCD là hình thoi nên ta có 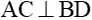 .
.
Ta có 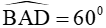 nên
nên 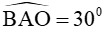 (tính chất đường chéo hình thoi)
(tính chất đường chéo hình thoi)
Tam giác ABO vuông tại O có
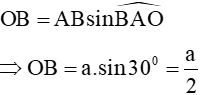
Xét tam giác vuông ABO có  ( hai góc phụ nhau) mà
( hai góc phụ nhau) mà 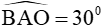 suy ra
suy ra 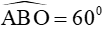 hay
hay 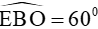
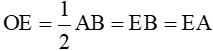
( tính chất đường trung tuyến trong tam giác vuông và E là trung điểm của AB.
Tam giác EOB là tam giác cân tại E có 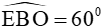 nên tam giác EBO là tam giác đều
nên tam giác EBO là tam giác đều
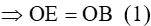
Chứng minh tương tự với các tam giác vuông BOC ta có OB = OF (2)
Chứng minh tương tự với các tam giác vuông COD ta có OD = OG (3)
Chứng minh tương tự với các tam giác vuông DOA ta có OD = OH (4)
Mà OD = OB ( vì O là tâm của hình thoi ABCD) nên kết hợp với (1), (2), (3),(4) ta có: OE = OB = OF = OC = OG = OD = OH
Vậy 6 điểm E, F, G, H, B, D cùng nằm trên một đường tròn tâm O. Bán kính 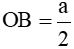
Ví dụ 2: Cho tam giác ABC vuông tại A. Trên AC lấy điểm D. Hình chiếu của D lên BC là E, điểm đối xứng của E qua BD là F. Chứng minh 5 điểm A, B, E, D, F cùng nằm trên một đường tròn. Xác định tâm O của đường tròn đó.
Giải
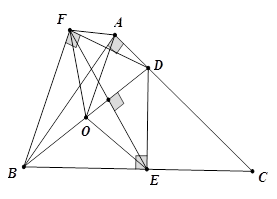
Do 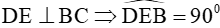
Vì E và F đối xứng với nhau qua BD nên BD là đường trung trực của đoạn thẳng EF
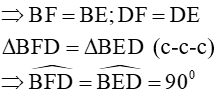
Gọi O là trung điểm của BD.
Xét tam giác vuông ABD vuông tại A có AO là trung tuyến nên
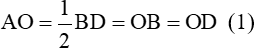
Tam giác vuông BDE vuông tại E có OE là trung tuyến nên
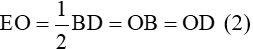
Tam giác vuông BFDvuông tại F có OF là trung tuyến nên
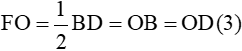
Từ (1), (2), (3)
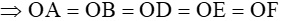
Vậy 5 điểm A, B, E, D, F cùng nằm trên một đường tròn tâm O với O là trung điểm của BC.
Dạng 2:Tứ giác nội tiếp
Phương pháp
Để chứng minh tứ giác nội tiếp ta có thể sử dụng một trong các phương pháp sau

Ví dụ 1: Cho tam giác ABC, 2 đường cao BB’, CC’. Chứng minh tứ giác BCB’C’ nội tiếp.
Giải
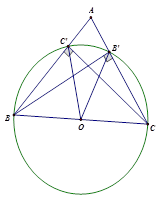
Gọi O là trung điểm của BC. Xét DBB’C có : 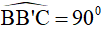 (giả thiết)
(giả thiết)
OB’ là đường trung tuyến ứng với cạnh huyền
⇒ OB’ = OB = OC = r (1)
Xét DBC’C có : 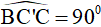 (giả thiết)
(giả thiết)
Tương tự trên ⇒ OC’ = OB = OC = r (2)
Từ (1) và (2) ⇒ B, C’, B’, C∈(O; r)⇒ Tứ giác BC’B’C nội tiếp đường tròn.
Ví dụ 2: Cho nửa đường tròn tâm O đường kính AB, kẻ tiếp tuyến Bx và lấy hai điểm C và D thuộc nửa đường tròn. Các tia AC và AD cắt Bx lần lượt ở E, F( F ở giữa B và E)
1. Chứng minh: 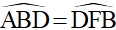 .
.
2. Chứng minh rằng CEFD là tứ giác nội tiếp.
Giải
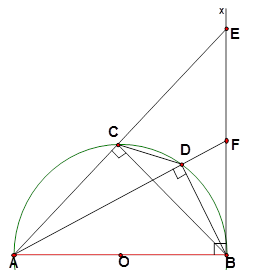
1) ΔADB có 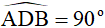 (góc nội tiếp chắn nửa đường tròn )
(góc nội tiếp chắn nửa đường tròn )
⇒ ΔDBF vuông tại D
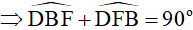 (vì tổng ba góc của một tam giác bằng 1800 )(1)
(vì tổng ba góc của một tam giác bằng 1800 )(1)
ΔABF có 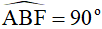 ( BF là tiếp tuyến ).
( BF là tiếp tuyến ).
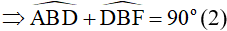
Từ (1) và (2)
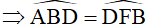
2) Tứ giác ACDB nội tiếp (O)
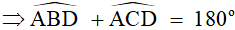
mà 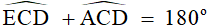 ( Vì là hai góc kề bù)
( Vì là hai góc kề bù)
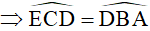
Theo trên
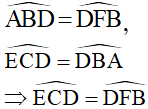
Mà 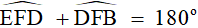 ( Vì là hai góc kề bù) nên
( Vì là hai góc kề bù) nên
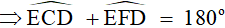
do đó tứ giác CEFD là tứ giác nội tiếp.
Dạng 3: Bài toán quĩ tích
Phương pháp
Để tìm quĩ tích các điểm M thỏa mãn tính chất α ta làm như sau:
- B1: Tìm hiểu bài toán, chỉ ra được các yếu tố sau đây
+ Yếu tố cố định: thông thường là các điểm
+Yếu tố không đổi: như độ dài đoạn thẳng , số đo góc, diện tích hình...
+Yếu tố thay đổi: thường là các điểm mà ta đi tìm quĩ tích hoặc các đoạn thẳng, các hình mà trên đó có điểm mà ta cần tìm quĩ tích. Các yếu tố này thường cho kèm nhóm từ( di động , di chuyển, chạy, thay đổi...)
- B2: Đoán nhận quĩ tích cần tìm: ta thường tìm 3 điểm của quĩ tích. Muốn vậy nên xét 3 vị trí đặc biệt, tốt nhất là sử dụng các điểm giới hạn, với điều kiện vẽ hình chính xác sẽ giúp ta hình dung được quĩ tích. Giả sử ta dự đoán quĩ tích các điểm M thỏa mãn tính chất α là hình H
- B3: Chứng minh kết quả tìm được ở bước 2. Ta phải chứng minh hai phần
+ Phần thuận: Mọi điểm có tính chất α đều thuộc hình H
+Phần đảo: Mọi điểm thuộc hình H đều có tính chất α
- B4: Kết luận
Ví dụ 1: Cho (O) và (O’) bằng nhau, cắt nhau tại A và B. Qua B vẽ một cát tuyến cắt các đường tròn (O) và (O’) lần lượt tại C và D.
- CMR : AC = AD.
- Tìm quỹ tích trung điểm M của CD khi cát tuyến CBD quay quanh B.
Giải
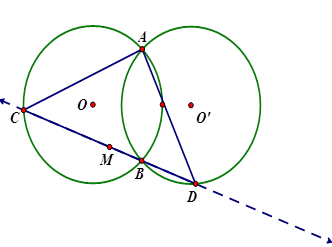
(O) có góc là góc nội tiếp chắn cung nhỏ AB. (O’) có góc là góc nội tiếp chắn cung nhỏ AB (O) và (O’) bằng nhau |
|
Tam giác ACD cân tại A có M là trung điểm của CD ⇒ AM vuông góc với CD
⇒M thuộc đường tròn đường kính AB. | |
Dạng 4: Các bài toán về đường tròn liên quan đến tiếp tuyến
Phương pháp
Để làm được các bài toán về đường tròn liên quan đến tiếp tuyến cần nắm được một số kiền thức sau đây
1. Tiếp tuyến của đường tròn
- Tiếp tuyến của đường tròn là đường thẳng chỉ có 1 điểm chung với đường tròn ( điểm chung đó được gọi là tiếp điểm)
- Nếu một đường thẳng là tiếp tuyến của đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm ( tại A, trong đó A là tiếp điểm)
- Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.
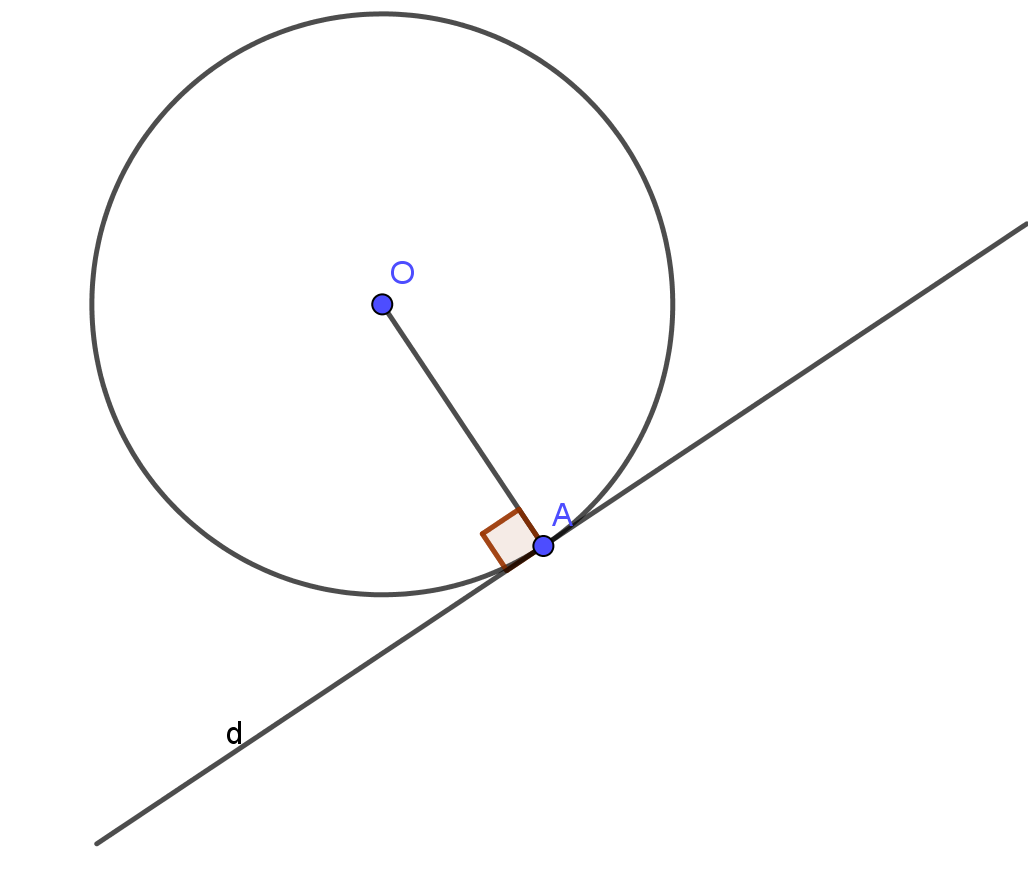
2. Tính chất của hai tiếp tuyến cắt nhau
- Nếu hai tiếp tuyến của một đường tròn cắt nhau tạo một điểm thì
+ Điểm đó cách đều hai tiếp điểm, tức là: MA = MB
+ Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến, tức là: 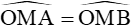
+ Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua tiếp điểm, tức là: 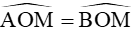
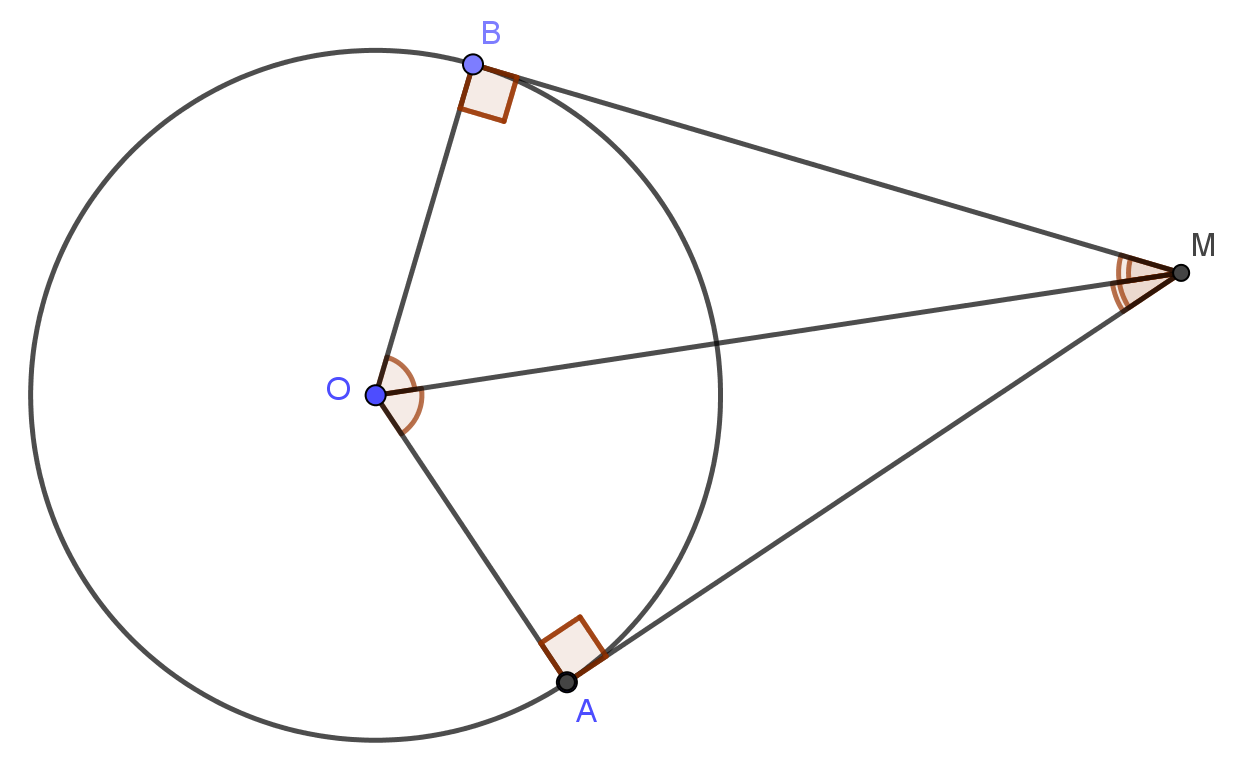
- Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với ba cạnh của tam giác, tam đường tròn nội tiếp tam giác là giao điểm của 3 đường phân giác trong của tam giác.
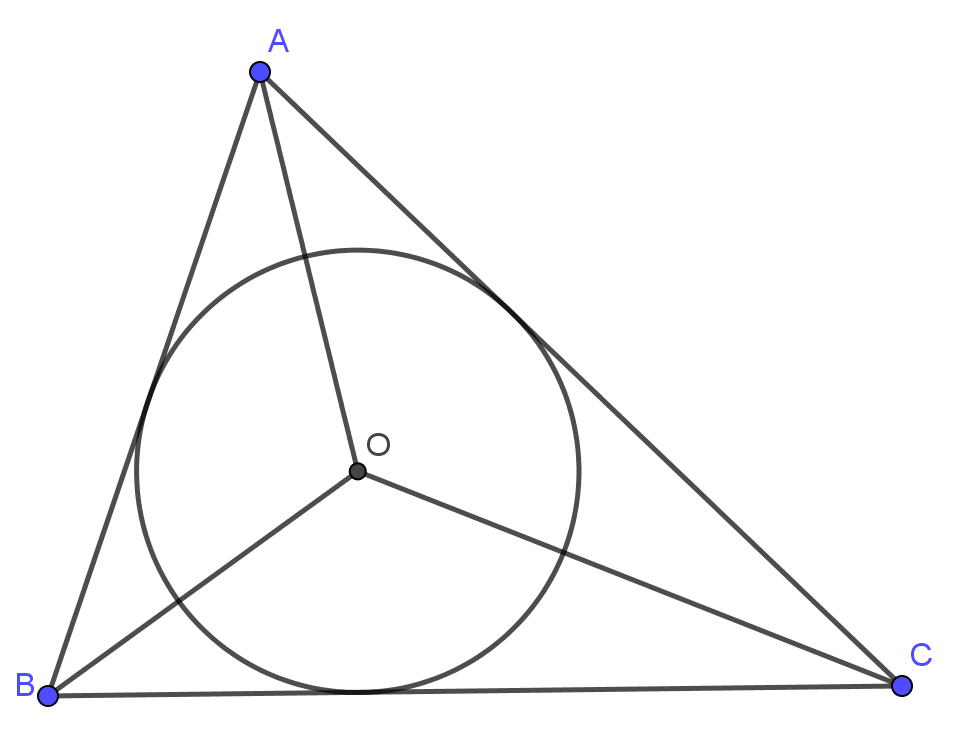
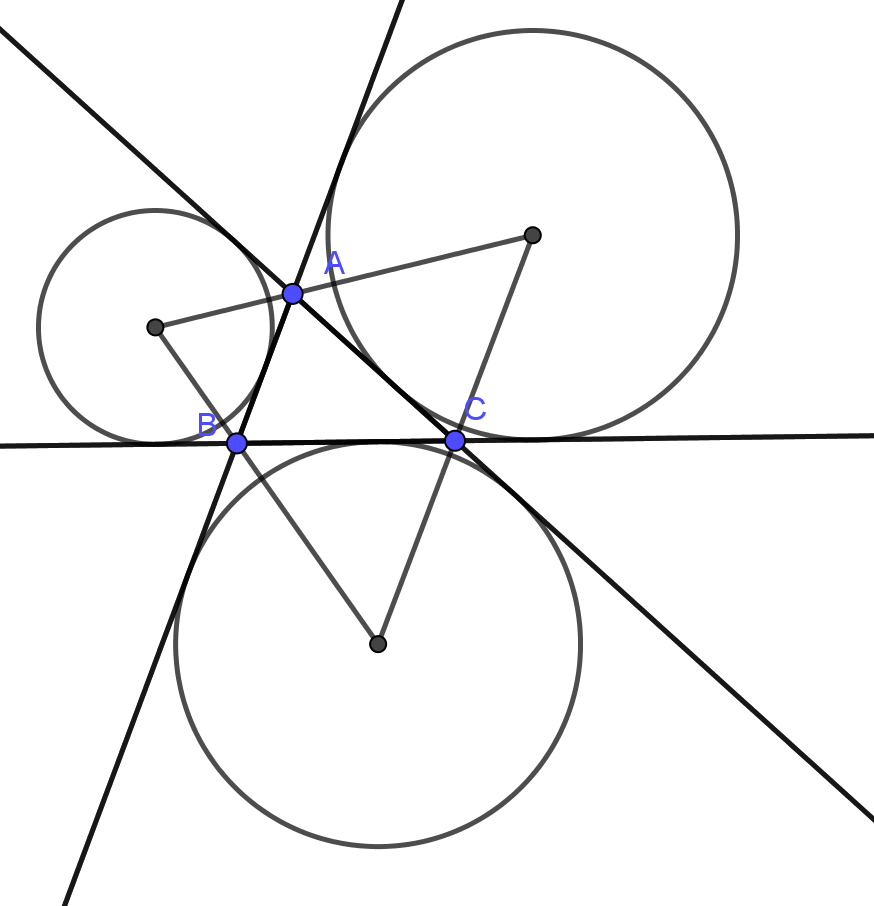
- Đường tròn bàng tiếp tam giác là đường tròn tiếp xúc với một cạnh của tam giác và phần kéo dài hai cạnh kia, tâm đường tròn này là gia của 2 đường phân giác của góc ngoài tam giác. Mỗi tam giác có 3 đường tròn bàng tiếp tam giác.
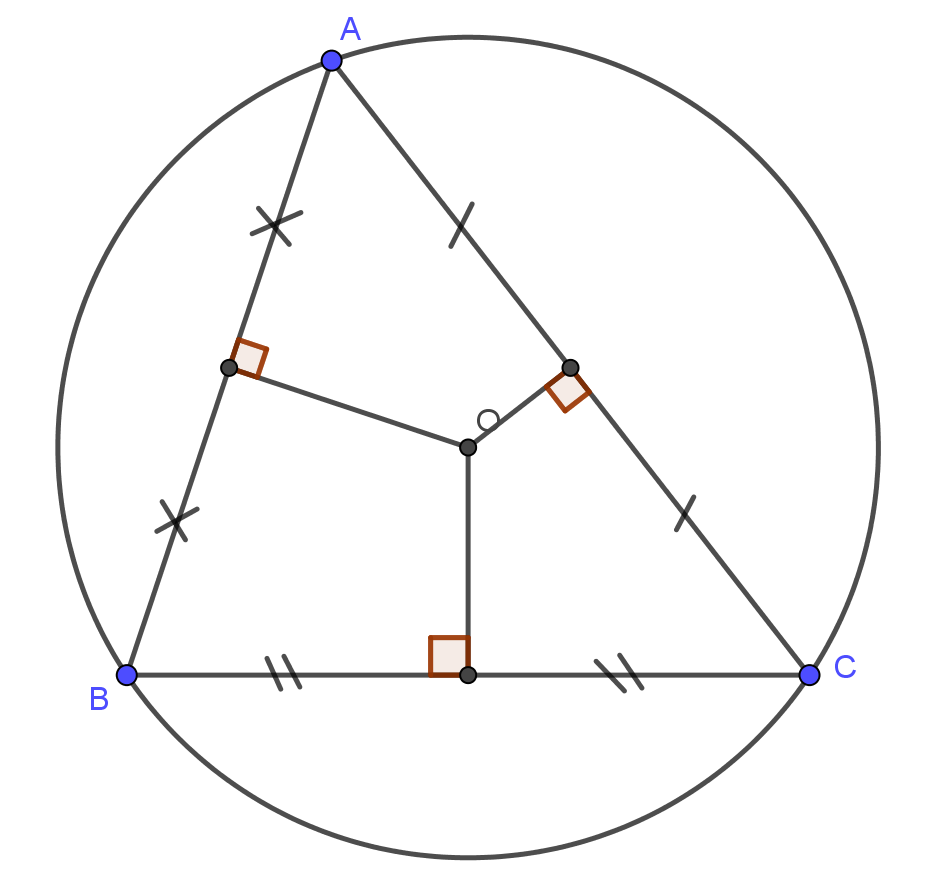
- Đường tròn ngoại tiếp tam giác là đường tròn đi qua 3 đỉnh của tam giác, tâm đường tròn này là giao của 3 đường trung trực của tam giác.
Ví dụ 1: Cho đường tròn tâm O, bán kính R và đường thẳng d tiếp xúc với đường tròn (O) tại A. Lấy điểm M bất kì trên đường thẳng d (M khác A). Qua điểm M kẻ tiếp tuyến MB với đường tròn (B là tiếp điểm, B khác A).
1) Chứng minh tứ giác OAMB nội tiếp.
2) Gọi I là giao điểm của AB và OM. Chứng minh rằng OI.OM = R2.
3) Gọi H là trực tâm của tam giác MAB.Tính chu vi tứ giác OAHB theo R.
Lời giải
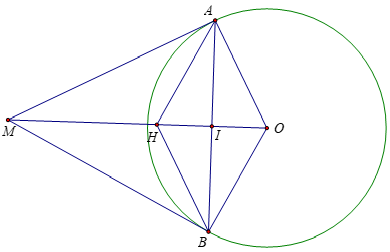
1) Vì MA là tiếp tuyến với đường tròn (O) tại A nên 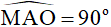
Vì MB là tiếp tuyến với đường tròn (O) tại B nên 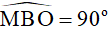
Tứ giác OAMB có: 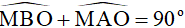 mà hai góc này là hai góc đối nên tứ giác OAMB nội tiếp.
mà hai góc này là hai góc đối nên tứ giác OAMB nội tiếp.
2) Theo (1) ta có tam giác OAM vuông tại A.
Ta có OA = OB = R và MA = MB (tính chất hai tiếp tuyến cắt nhau)
Do đó OM là đường trung trực của AB ⇒ OM vuông góc với AB tại I.
⇒ AI là đường cao của tam giác vuông OAM.
Áp dụng hệ thức lượng trong tam giác vuông ta có OI.OM = OA2.
Mà OA = R ⇒ OI.OM = R2.
3) Ta có AH // OB ( vì cùng vuông góc với BM),BH // OA ( vì cùng vuông góc với MA).
Suy ra tứ giác OAHB là hình bình hành.
Mà 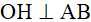 ⇒ OAHB là hình thoi OB = OA = HA = HB = R
⇒ OAHB là hình thoi OB = OA = HA = HB = R
Do đó chu vi tứ giác OAHB là: OB + OA + HA + HB = 4R.
Ví dụ 2: Cho đường tròn tâm O, bán kính R, dây cung MN( MN < 2R). Trên tia đối của tia MN lấy điểm A. Từ A kẻ tiếp tuyến AB, AC tới đường tròn (O) (B, C là tiếp điểm).
1) Chứng minh bốn điểm A, B, O, C cùng thuộc một đường tròn.
2) Chứng minh AB2 = AC2 = AM.AN
Lời giải
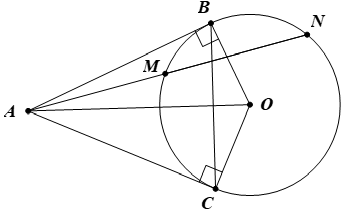
1) AB, AC lần lượt là tiếp tuyến của đường tròn (O) tại B và C (giả thiết)
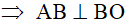 tại B;
tại B;  tại C (tính chất của tiếp tuyến )
tại C (tính chất của tiếp tuyến )
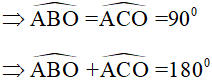
⇒Tứ giác ABOC nội tiếp (dấu hiệu nhận biết)
⇒Bốn điểm A, B, O, C cùng thuộc một đường tròn (định nghĩa).
2) AB, AC lần lượt là tiếp tuyến của đường tròn (O) tại B và C (giả thiết)
⇒AB=AC (tính chất hai tiếp tuyến cắt nhau) ⇒AB2=AC2 (1)
Ta có  là góc tạo bởi tia tiếp tuyến và dây cung chắn cung BM
là góc tạo bởi tia tiếp tuyến và dây cung chắn cung BM
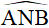 là góc nội tiếp chắn cung BM
là góc nội tiếp chắn cung BM
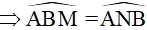 (tính chất)
(tính chất)
Xét ΔABM và ΔABN có :

Dạng 5: Tính độ dài cạnh, góc. Chứng minh đẳng thức giữa cạnh và góc
Phương pháp
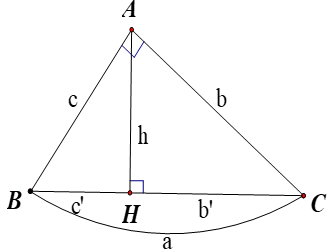
- Để làm được dạng toán này ta cần nắm được hệ thức góc và cạnh trong tam giác
Cho tam giác ABC vuông tại A, đường cao AH. Khi đó ta có các hệ thức sau:
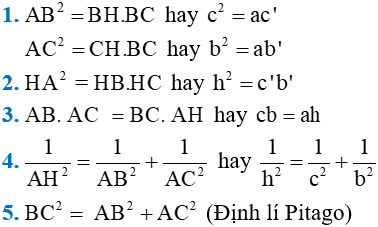

- Một số dạng toán thường gặp
+ Tính độ dài các đoạn thẳng trong tam giác vuông
Phương pháp giải là: Cho tam giác ABC vuông tại A đường cao AH. Nếu biết độ dài hai trong sáu đoạn thẳng AB, AC, BC, HA, HB, HC thì ta luôn tính được độ dài bốn đoạn thẳng còn lại bằng việc vận dụng các hệ thức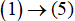
+ Chứng minh các hệ thức liên quan đến tam giác vuông
Phương pháp giải: Sử dụng các hệ thức về cạnh và đường cao một cách hợp lý theo hướng:
Bước 1. Chọn các tam giác vuông thích hợp chứa các đoạn thẳng có trong hệ thức.
Bước 2. Tính các đoạn thẳng đó nhờ hệ thức về cạnh và đường cao.
Bước 3. Liên kết các giá trị trên để rút ra hệ thức cần chứng minh.
Ví dụ 1: Cho tam giác ABC vuông tại A, AH là đường cao. Biết AB = 8cm, AC = 6cm. Tính độ dài AH.
Giải
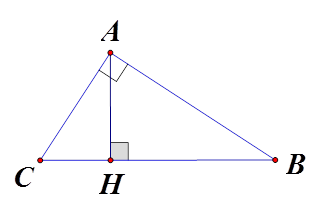
Ta có vuông tại A nên :
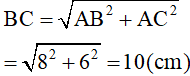
(Định lý Pytago)
ΔABC vuông tại A, AH ⊥ BC, nên
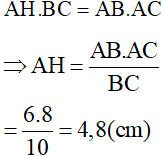
Ví dụ 2: Cho tam giác ABC cân tại A. Các tia phân giác của góc A và góc B cắt nhau tại O. Biết 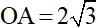 cm, OB = 2cm, tính độ dài AB.
cm, OB = 2cm, tính độ dài AB.
Giải
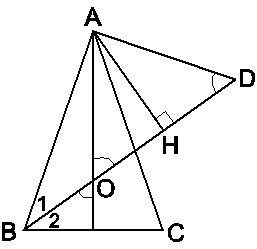
Qua A vẽ một đường thẳng vuông góc với AB cắt tia BO tại D.
Ta có ΔABD vuông tại A
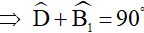
ΔABC cân tại A nên AO là phân giác đồng thời cũng là đường cao
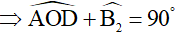
mà 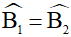 nên
nên 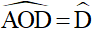
Do đó ΔAOD cân tại A. Suy ra 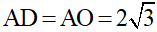 (cm).
(cm).
Vẽ AH ⊥ OD thì HO = HD.
Ta đặt HO=HD=x thì BD=2x+2
Xét ΔABD vuông tại A, đường cao AH, ta có AD2=BD.HD
Suy ra 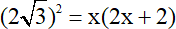 .Từ đó ta được phương trình:
.Từ đó ta được phương trình:
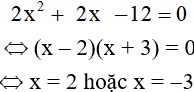
Giá trị x = 2 được chọn, giá trị x = -3 bị loại.
Do đó BD=2+2+2=6 (cm).
Suy ra 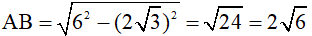 (cm).
(cm).
Ví dụ 3: Cho tam giác ABC vuông tại A . Chứng minh rằng
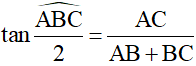
Giải

Vẽ đường phân giác BD của ΔABC ( D ∈ AC ).
Theo tính chất đường phân giác của tam giác ta có :
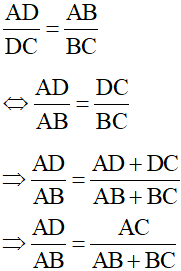 (1)
(1)
Xét ΔABD có
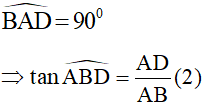
Từ (1) và (2)
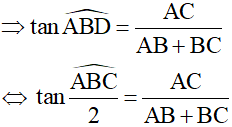
Vậy 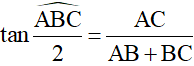
Dạng 6: Chứng minh tam giác đồng dạng
Phương pháp
Để chứng minh ΔABC đồng dạng với ΔMNP ta làm như sau:
- Cách 1: Chứng minh ba cạnh của tam này tỉ lệ với ba cạnh của tam giác kia
Tức là ta chứng minh
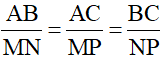
-Cách 2: Chứng minh hai góc của tam này bằng hai góc của tam giác kia
Tức là ta chứng minh:
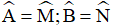
- Cách 3: Chứng minh hai cạnh của tam này tỉ lệ với hai cạnh của tam giác kia và góc xen giữa hai cạnh đó bằng nhau
Tức là ta chứng minh
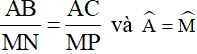
Chú ý: Các trường hợp đồng dạng của tam giác vuông
- TH1: Nếu cạnh huyền và cạnh góc vuông của tam giác này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác kia thì hai tam giác vuông đồng dạng
- TH2: Nếu hai cạnh góc vuông của tam giác này tỉ lệ với hai cạnh góc vuông của tam giác kia thì hai tam giác vuông đồng dạng
- TH3: Nếu góc nhọn của tam giác này bằng góc nhọn của tam giác kia thì hai tam giác vuông đồng dạng
Ví dụ 1: Cho tứ giác ABCD nội tiếp đường tròn . Gọi I là giao điểm AC và BD. Kẻ IH vuông góc với AB; IK vuông góc với AD (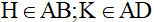 ).
).
a) Chứng minh tứ giác AHIK nội tiếp đường tròn.
b) Chứng minh rằng 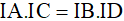 .
.
c) Chứng minh rằng tam giác HIK và tam giác BCD đồng dạng.
Giải
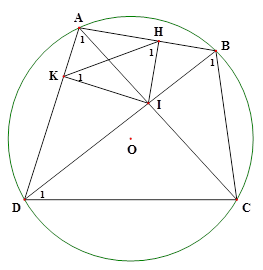
a) Chứng minh tứ giác AHIK nội tiếp đường tròn.
Xét tứ giác AHIK có:

b) Chứng minh rằng 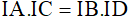 .
.
Xét ΔIAD và ΔIBC có:
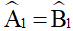 (2 góc nội tiếp cùng chắn cung DC của (O))
(2 góc nội tiếp cùng chắn cung DC của (O))
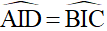 (2 góc đối đỉnh)
(2 góc đối đỉnh)
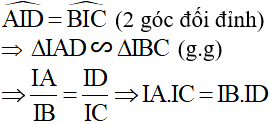
c) Chứng minh rằng tam giác HIK và tam giác BCD đồng dạng.
Xét đường tròn ngoại tiếp tứ giác AHIK có
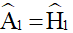 (2 góc nội tiếp cùng chắn cung IK)
(2 góc nội tiếp cùng chắn cung IK)
Mà 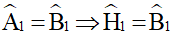
Chứng minh tương tự, ta được 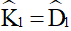
ΔHIK và ΔBCD có: 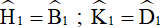
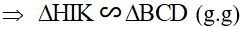
Ví dụ 2: Cho ΔABC có ba góc nhọn nội tiếp đường tròn (O). Đường cao CD của cắt đường tròn (O) tại E. Từ B kẻ 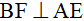 tại F.
tại F.
a) Chứng minh tứ giác BDEF nội tiếp được đường tròn.
b) Kẻ đường cao BK của ΔABC . Chứng minh 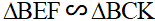
Giải
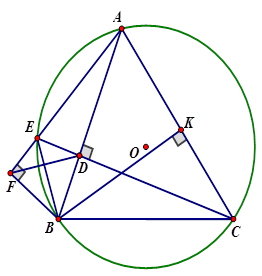
a) Xét tứ giác BDEF, ta có:
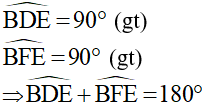
Vậy tứ giác BDEF nội tiếp được đường tròn.
b) Ta có: tứ giác ACBE nội tiếp đường tròn (O)

A, E, F thẳng hàng nên

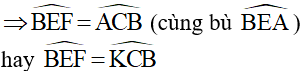
Hai tam giác vuông ΔBEF,ΔBCK có một góc nhọn bằng nhau nên
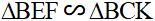
Dạng 7: Chứng minh đường thẳng vuông góc , song song
1. Phương pháp chứng minh hai đường thẳng vuông góc
- Cách 1:Chứng minh hai đường thẳng đó cắt nhau tạo ra một góc
- Cách 2: Chứng minh hai đường đó chứa hai tia phân giác của hai góc kề bù
- Cách 3: Chứng minh hai đường đó chứa hai cạnh của tam giác vuông
- Cách 4: Sử dụng tính chất đường trung trực của đoạn thẳng
- Cách 5: Sử dụng tính chất trực tâm của tam giác
- Cách 6: Sử dụng tính chất đường kính và dây cung
- Cách 7: Sử dụng tính chất tiếp tuyến trong hình tròn
- Cách 8: Chứng minh hai đường đó chứa hai đường chéo của hình vuông hoặc hình thoi
- Cách 9: Sử dụng mối quan hệ song song và vuông góc của đường thẳng
2. Phương pháp chứng minh hai đường thẳng song song
- Chứng minh các góc so le trong, đồng vị bằng nhau
- Sử dụng tính chất bắc cầu: hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau
- Dùng tính chất từ vuông góc đến song song: hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì song song với nhau
- Sử dụng tính chất của hình bình hành, hình chữ nhật, hình vuông, hình thoi
- Sử dụng tính chất đường trung bình của tam giác, hình thang, hình bình hành
- Sử dụng định lý Ta-let đảo
- Sử dụng phương pháp chứng minh phản chứng
Ví dụ 1: Cho ∆ABC nhọn, nội tiếp đường tròn đường tròn tâm O bán kính R, AK là đường kính. Vẽ các đường cao AD, BE, CF của ∆ABC.
a) Chứng minh: Tứ giác BCEF nội tiếp.
b) Gọi M là hình chiếu vuông góc của C trên AK. Chứng minh: MD //BK.
Lời giải
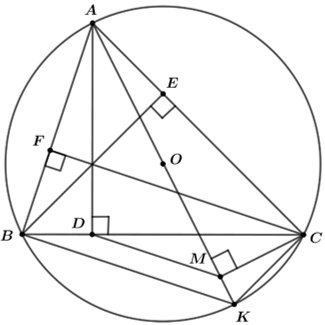
a) Vì BE là đường cao của ∆ABC .
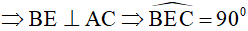
Vì CF là đường cao của ∆ABC .
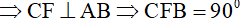
Xét tứ giác BCEF có hai đỉnh kề nhau E, Fcùng nhìn cạnh BC dưới 1 góc bằng 900⇒ tứ giác BCEF nội tiếp.
b) Vì AD là đường cao của ∆ABC .
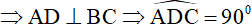
M là hình chiếu của C lên AK .
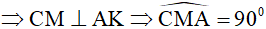
Xét tứ giác ADMC có hai đỉnh kề nhau D, M cùng nhìn cạnh AC dưới góc 900 ⇒ tứ giác ADMC nội tiếp
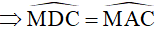 (góc nội tiếp cùng chắn cung AC). (1)
(góc nội tiếp cùng chắn cung AC). (1)
Ta lại có: 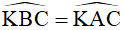 hay
hay 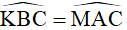 (góc nội tiếp cùng chắn cung KC) (2)
(góc nội tiếp cùng chắn cung KC) (2)
Từ (1) và (2) 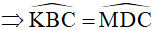 , mà hai góc này ở vị trí đồng vị
, mà hai góc này ở vị trí đồng vị
Suy ra DM // BK (đpcm).
Ví dụ 2: Cho tam giác ABC nội tiếp đường tròn (O). Tia phân giác góc A cắt BC tại D và cắt đường tròn tại điểm thứ hai là M. Kẻ tiếp tuyến AK với đường tròn (M, MB), K là tiếp điểm. Chứng minh rằng DK vuông góc với AM.
Giải
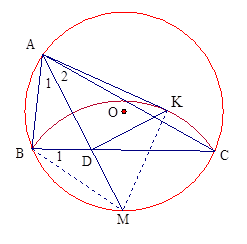
Ta có  ( góc nội tiếp cùng chắn cung MC) nên
( góc nội tiếp cùng chắn cung MC) nên 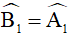 hay
hay 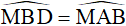
Xét ∆MBD và ∆MAB có 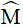 chung và
chung và
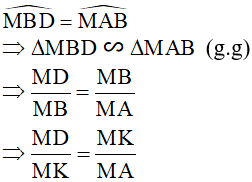
Kết hợp với 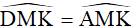 (góc chung)
(góc chung)
ta có:
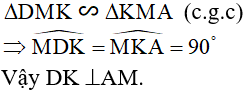
Bài tập vận dụng
Bài 1: Cho hình vuông ABCD. Trên cạnh BC, AD lần lượt lấy các điểm E, F sao cho 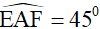 . Biết BD cắt AE, AF theo thứ tự tại G, H. Chứng minh rằng
. Biết BD cắt AE, AF theo thứ tự tại G, H. Chứng minh rằng
a) ADFG; GHFE là các tứ giác nội tiếp
b) Tam giác CGH và tứ giác GHFE có diện tích bằng nhau
Bài 2: Cho tam giác ABC cân tại A nội tiếp đường tròn (O). Trên tia đối của tia AB lấy điểm D sao cho AD = AC.
a) Chứng minh rằng 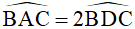
b) Gọi M là điểm trên cung AC, trên tia đối của tia MB lấy điểm E sao cho ME = MC. Chứng minh rằng bốn điểm B; D; E; C thuộc một đường tròn
Bài 3: Trên đường tròn (O) lấy hai điểm B và D. Gọi A là điểm chính giữa cung lớn BD. Các tia AD, AB cắt tiếp tuyến Bx và Dy của đường tròn lần lượt tại N và M. Chứng minh.
a)Tứ giác BDNM nội tiếp đường tròn
b) MN// BD
Bài 4: Cho đường tròn (O;R) có AB là đường kính cố định, còn CD kà đường kính thay đổi. Gọi (d) là tiếp tuyến của đường tròn tại B; AC, AD lần lượt cắt (d) tại P, Q.Chứng minh tứ giác CPQD nội tiếp được đường tròn
Bài 5: Từ điểm A bên ngoài đường tròn (O) vẽ hai tiếp tuyến AB; AC và cát tuyến AMN. Gọi I là trung điểm của MN.
a) Chứng minh AB2 = AM . AN
b) Chứng minh rằng 5 điểm A, B, I, C, O cùng nằm trên một đường tròn
Bài 6: Cho ba điểm A, B, C nằm trên đường thẳng xy theo thứ tự đó. Vẽ đường tròn (O) đi qua hai điểm B và C. Từ điểm A vẽ hai tiếp tuyến AM, AN (M, N thuộc đường tròn). Gọi E là hình chiếu của O trên xy; AO cắt MN tại F.
a) Chứng minh AM2 = AB . AC
b) Chứng minh 5 điểm A, N, O, E, M cùng nằm trên một đường tròn
.
Bài 7: Từ điểm A ở bên ngoài đường tròn (O) vẽ hai tiếp tuyến AN, AM. Trên nửa mặt phẳng bờ AN không chứa M lấy điểm B sao cho  . Đường thẳng BO cắt AN tại D, cắt đường thẳng AM tại C. Đường thẳng BM cắt AN tại K. Gọi I là trung điểm của AC. BI cắt AN tại E. Chứng minh năm điểm A, B, N, O, M cùng nằm trên một đường tròn.
. Đường thẳng BO cắt AN tại D, cắt đường thẳng AM tại C. Đường thẳng BM cắt AN tại K. Gọi I là trung điểm của AC. BI cắt AN tại E. Chứng minh năm điểm A, B, N, O, M cùng nằm trên một đường tròn.
Bài 8: Cho hình vuông ABCD và một điểm M trên cạnh BC. Vẽ hình vuông AMPQ sao cho P và Q thuộc cùng một nửa mặt phẳng bờ AM không chứa đỉnh B. Chứng minh rằng:
a) Ba điểm Q, C, D thẳng hàng
b) Năm điểm A, M, C, P, Q cùng thuộc một đường tròn
Bài 9: Cho đường tròn tâm O bán kình bằng 6cm, điểm A nằm trên đường tròn. Qua A kẻ tiếp tuyến Ax, trên đó lấy điểm B sao cho AB = 8cm.
a) Tính OB.
b) Qua A kẻ đường vuông góc OB cắt đường tròn tâm O ở C. Chứng minh rằng BC là tiếp tuyến của đường tròn
Bài 10: Cho đường tròn tâm O và điểm B tùy ý trên đường tròn. Qua B kẻ tiếp tuyến với đường tròn, trên đó lấy điểm A. Trên AO lấy điểm C sao cho AC = BC, tia BC cắt đường tròn tâm O ở E. Chứng minh rằng 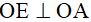 .
.
Bài 11: Cho đường tròn tâm O, bán kính 5cm, đường kinh AB, tiếp tuyến Bx. Gọi C là một điểm trên đường tròn sao cho 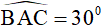 , tia AC cắt Bx ở E.
, tia AC cắt Bx ở E.
a) Chứng minh BC2 = AC.CE
b) Tính BE.
Bài 12: Cho đường tròn tâm O, bán kính R, đường kính AB, M là một điểm nằm giữa O và B. Đường thẳng kẻ qua trung điểm E của AM vuông góc với AB cắt đường tròn tâm O ở C và D.
a) Tứ giác ACMD là hình gì?
b) Kẻ tiếp tuyến với đường tròn tại C, tiếp tuyến này cắt OA tại I. Chứng minh rằng ID là tiếp tuyến của đường tròn tâm O, bán kính R.
Bài 13: Tính diện tích của 1 tam giác cân có chiều cao tương ứng với đáy bằng 10cm, chiều cao ứng với cạnh bên bằng 12cm
Bài 14: Cho tam giác ABC vuông tại A, đường cao AH. Gọi M, N lần lượt là hình chiếu của H trên AB và AC. Cmr:
a) AM.AB = BH.HC
b) AM.AB = BH.HC
c) HB.HC = MA.MB + NA.NC
d) 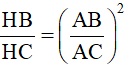
Bài 15. Cho đường tròn (O) đường kính AB = 2R . Điểm C nằm trên (O) mà AC > BC. Kẻ CD ⊥ AB ( D ∈ AB ). Tiếp tuyến tại A của đường tròn (O) cắt BC tại E. Tiếp tuyến tại C của đường tròn (O) cắt AE tại M. OM cắt AC tại I . MB cắt CD tại K.
a) Chứng minh M là trung điểm AE.
b) Chứng minh IK // AB.
Bài 16. Cho ba điểm A, B,C nằm trên đường thẳng xy theo thứ tự đó. Vẽ đường tròn (O) đi qua B và C. Từ A vẽ hai tiếp tuyến AM và AN . Gọi E và F lần lượt là trung điểm của BC và MN.
a) Chứng minh AM2 = AN2 = AB. AC
b) Đường thẳng ME cắt đường tròn (O) tại I. Chứng minh IN // AB
c) Chứng minh rằng tâm đường tròn ngoại tiếp tam giác OEF nằm trên một đường thẳng cố định khi đường tròn (O) thay đổi
Bài 17: Cho đường tròn tâm O, hai dây cung AC và BD bằng nhau cắt nhau tại E. Chứng minh rằng
a) EB = EC, EA = ED
b) 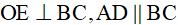
c) AB = CD
Bài 18: Tam giác ABC nội tiếp đường tròn tâm O. Các điểm M, N, P là điểm chính giữa của các cung AB, BC, CA. Gọi D là giao điểm của MN và AB, E là giao điểm của PN và AC. Chứng minh rằng DE song song với BC.
Bài 19: Từ điểm M ở ngoài đường tròn (O), vẽ hai tiếp tuyến MA, MB và một cát tuyến MCD. Gọi I là giao điểm của AB và CD. Chứng minh rằng: 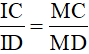 .
.
Bài 20:Cho tứ giác ABCD có bốn đỉnh thuộc đường tròn . Gọi M, N, P, Q lần lượt là điểm chính giữa các cung AB, BC, CD, DA. Chứng minh rằng 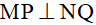 .
.
Bài 21: Cho tam giác ABC vuông cân tại A, nội tiếp trong đường tròn tâm O. Tiếp tuyến tại B với đường tròn (O) cắt tia CA tại D. Trên cạnh AB lấy điểm E (E không trùng với A và B). Tia CE cắt đường tròn (O) tại F và cắt BD tạị K. Tia BF cắt CD tại M.
a) Chứng minh 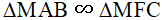 .
.
b) Chứng minh tứ giác AFKD nội tiếp.
c) Tia ME cắt BC tại H. Tứ giác MDBH là hình gì?
d) Chứng minh 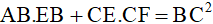 .
.
Bài 22: Cho đường tròn (O;R) đường kính AB = 2R dây cung MN của (O) vuông góc với AB tại I sao cho IA < IB. Trên đoạn MI lấy điểm 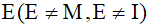 . Tia AE cắt đường tròn tại điểm thứ hai là K
. Tia AE cắt đường tròn tại điểm thứ hai là K
a) Chứng minh tứ giác IEKB nội tiếp được đường tròn.
b) Chứng minh AM2 = AE. AK
c) Chứng minh 
Bài 23: Cho nửa đường tròn tâm O, đường kính AB = 2R. Trên tia đối của tia AB lấy điểm E (khác với điểm A). Tiếp tuyến kẻ từ điểm E cắt các tiếp tuyến kẻ từ điểm A và B của nửa đường tròn (O) lần lượt tại C và D. Gọi M là tiếp điểm của tiếp tuyến kẻ từ điểm E.
a) Chứng minh rằng tứ giác ACMO nội tiếp được trong một đường tròn.
b) Chứng minh rằng 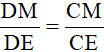
Bài 24: Cho (O) đường kính AB = 2R, xy là tiếp tuyến với (O) tại B. CD là một đường kính bất kỳ (AC<CB) . Gọi giao điểm của AC, AD với xy theo thứ tự là M và N.
1) Chứng minh rằng tứ giác MCDN nội tiếp.
2) Chứng minh AC.AM = AD.AN
3) Gọi I là tâm đường tròn ngoại tiếp tứ giác MCDN và H là trung điểm của MN. Chứng minh rằng tứ giác AOIH là hình bình hành. Khi đường kính CD quay xung quanh điểm O thì I di động trên đường nào?
Bài 25: Cho điểm M cố định nằm bên ngoài đường tròn (O; R). Qua M vẽ các tiếp tuyến MA, MB với đường tròn (O) (với A, B là các tiếp điểm). Gọi C là điểm bất kì trên cung nhỏ AB của đường tròn (O). Gọi D, E, F lần lượt là chân đường vuông góc kẻ từ C đến AB, MA, MB.
1) Chứng minh bốn điểm A, D, C, E cùng thuộc một đường tròn.
2) AC cắt DE tại P; BC cắt DF tại Q. Chứng minh đồng dạng với suy ra
3) Chứng minh AB // PQ
4) Khi điểm C di động trên cung nhỏ AB của đường tròn (O) thì trọng tâm G của tam giác ABC di chuyển trên đường nào?
Xem thử Đề ôn vào 10 Xem thử Đề vào 10 Hà Nội Xem thử Đề vào 10 TP.HCM Xem thử Đề vào 10 Đà Nẵng
Xem thêm bộ tài liệu các dạng bài tập ôn thi vào lớp 10 môn Toán chọn lọc, hay khác:
- Các dạng toán thực tế ôn thi vào lớp 10 năm 2025
- Các dạng Toán nâng cao ôn thi vào lớp 10 năm 2025
- Cấu trúc đề thi vào lớp 10 môn Toán năm 2025
- Cấu trúc đề thi vào lớp 10 môn Toán năm 2025 Hà Nội
- Cấu trúc đề thi vào lớp 10 Toán năm 2025 TP.HCM
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Đề thi lớp 1 (các môn học)
- Đề thi lớp 2 (các môn học)
- Đề thi lớp 3 (các môn học)
- Đề thi lớp 4 (các môn học)
- Đề thi lớp 5 (các môn học)
- Đề thi lớp 6 (các môn học)
- Đề thi lớp 7 (các môn học)
- Đề thi lớp 8 (các môn học)
- Đề thi lớp 9 (các môn học)
- Đề thi lớp 10 (các môn học)
- Đề thi lớp 11 (các môn học)
- Đề thi lớp 12 (các môn học)
- Giáo án lớp 1 (các môn học)
- Giáo án lớp 2 (các môn học)
- Giáo án lớp 3 (các môn học)
- Giáo án lớp 4 (các môn học)
- Giáo án lớp 5 (các môn học)
- Giáo án lớp 6 (các môn học)
- Giáo án lớp 7 (các môn học)
- Giáo án lớp 8 (các môn học)
- Giáo án lớp 9 (các môn học)
- Giáo án lớp 10 (các môn học)
- Giáo án lớp 11 (các môn học)
- Giáo án lớp 12 (các môn học)

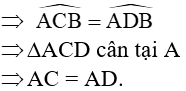



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

