Các dạng bài Giải phương trình (ôn thi vào lớp 10 Toán 2024)

Tài liệu Các dạng bài Giải phương trình ôn thi vào lớp 10 Toán năm 2024 có lời giải chi tiết giúp học sinh củng cố kiến thức, ôn luyện để chuẩn bị tốt cho kì thi tuyển sinh vào lớp 10 môn Toán.

Các dạng bài Giải phương trình (ôn thi vào lớp 10 Toán 2024)

Xem thử Đề ôn vào 10 Xem thử Đề vào 10 Hà Nội Xem thử Đề vào 10 TP.HCM Xem thử Đề vào 10 Đà Nẵng

Chỉ từ 150k mua trọn bộ Đề ôn thi vào 10 môn Toán năm 2024 bản word có lời giải chi tiết:

• B1: gửi phí vào tk: 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án

GIẢI PHƯƠNG TRÌNH ÔN THI VÀO LỚP 10

Dạng 1: Giải phương trình chứa căn thức (phương trình vô tỉ)

1. Giải bằng phương pháp bình phương hai vế

Phương pháp                                                                                

          -B1: Đặt điều kiện cho phương trình

          -B2: Bình phương hai vế thu được phương trình hệ quả

          -B3: Giải phương trình hệ quả, tìm nghiệm

          -B4: Đối chiếu nghiệm tìm được với điều kiện rồi kết luận

Ví dụ: Giải phương trình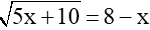

Giải

Điều kiện:

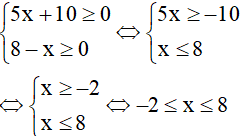
Phương trình

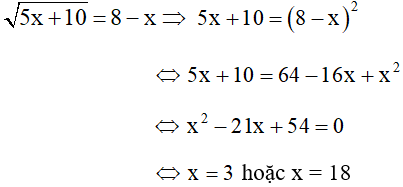
Ta thấy x = 3 thỏa mãn điều kiện (nhận)

Ta thấy x = 18 không thỏa mãn điều kiện (loại)

Vậy phương trình có một nghiệm x = 3

2. Giải bằng cách đưa về phương trình tích

Phương pháp

-B1: Đặt điều kiện cho phương trình

          -B2: Biến đổi đưa phương trình đã cho về phương trình tích bằng việc sử dụng một số đẳng thức sau

          u + v = 1 + uv ⇔(u – 1)(v – 1) = 0

au + bv = ab + uv ⇔(u – b)(v – a) = 0

          -B3: Giải từng phương trình tích tìm nghiệm

          -B4: Đối chiếu nghiệm tìm được với điều kiện rồi kết luận

Ví dụ: Giải phương trình 

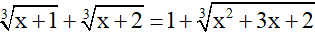 (1)

Giải

Ta có

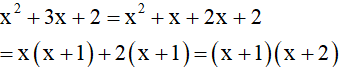
⇒Phương trình:

(1)

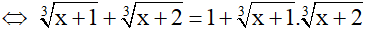
(dạng u + v = 1 + uv)

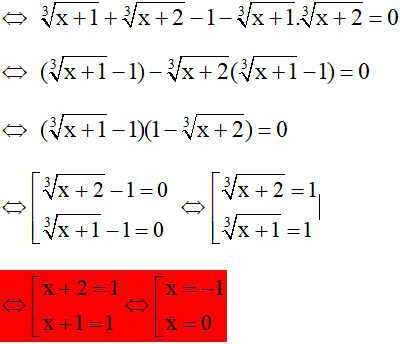
Vậy phương trình có 2 nghiệm x = 0, x = -1

3. Giải bằng cách dùng hằng đẳng thức

Phương pháp         

          - B1: Biến đổi biểu thức dưới dấu căn về dạng: (a-b)² hoặc (a+b)² hoặc (a-b)³ hoặc (a+b)³

          -B2: Sử dụng công thứ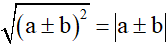c hoặc 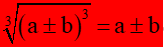 để khử dấu căn

          -B3: Giải phương trình và kết luận

Ví dụ: Giải phương trình

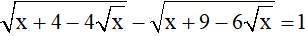
Giải

Vì 

nên phương trình đã cho tương đương với

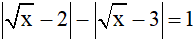
Điều kiện: x ≥ 0

TH1: nếu

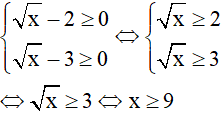
 thì phương trình trở thành

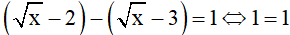
⇒phương trình có vô số nghiệm x ≥ 0

TH2: 

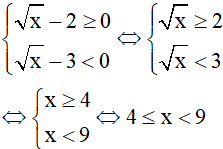
thì phương trình trở thành

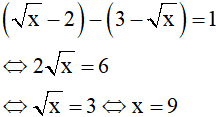
(không thỏa mãn 4 ≤ x < 9)

⇒loại

TH3:

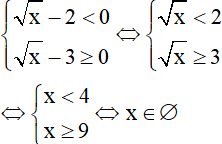
⇒phương trình vô nghiệm

TH4: 

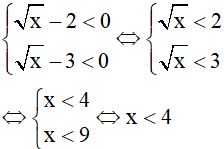
thì phương trình trở thành

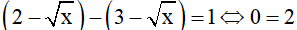
⇒phương trình vô nghiệm 

Vậy phương trình có vô số nghiệm x ≥ 0 

Dạng 2: Giải phương trình bằng cách đặt ẩn phụ

1. Đặt ẩn phụ hoàn toàn

Phương pháp 

-B1: Đặt điều kiện cho phương trình (nếu có)

          -B2: Biến đổi phương trình đã cho (nếu cần), đặt ẩn phụ và đưa ra điều kiện cho ẩn phụ

          Đưa phương trình đã cho về phương trình mới hoàn toàn theo ẩn phụ

          -B3: Giải phương trình mới tìm ẩn phụ

          -B4: Thay giá trị của ẩn phụ vào biểu thức đặt ẩn phụ ở B2 để tìm ẩn ban đầu

          - B5: Đối chiếu nghiệm tìm được với điều kiện sau đó kết luận

Ví dụ: Giải phương trình  (x + 1)⁴ + (x + 3)⁴ = 2 (1)

Giải

Đặt t = x + 2 .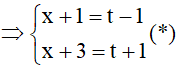

Thay (*) vào phương trình (1) ta được

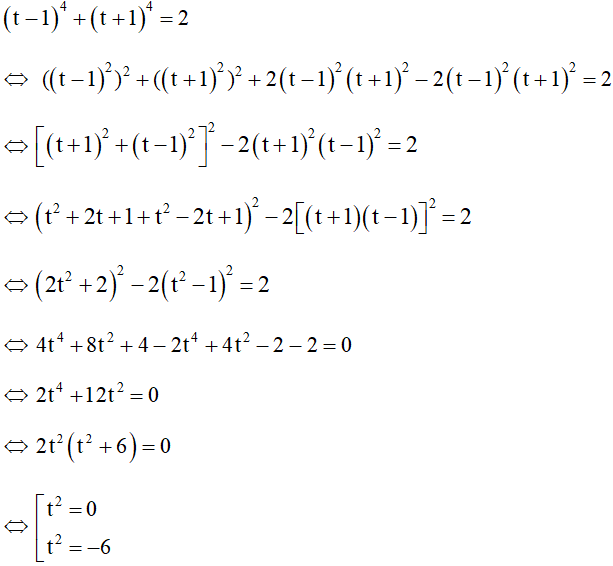
Với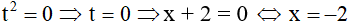

Với t² = -6 ( phương trình vô nghiệm)  

Vậy phương trình có nghiệm duy nhất  x = -2

2. Đặt ẩn phụ không hoàn toàn

Phương pháp 

-B1: Đặt điều kiện cho phương trình (nếu có)

          -B2: Biến đổi phương trình đã cho (nếu cần), đặt ẩn phụ và đưa ra điều kiện cho ẩn phụ

          Đưa phương trình đã cho về phương trình vừa chứa ẩn cũ vừa chứa ẩn phụ

          -B3: Giải phương trình ở bước 2 tìm mối liên hệ giữa ẩn cũ và ẩn phụ 

          -B4: Kết hợp kết quả tìm được ở bước 3 với biểu thức đặt ẩn phụ ở bước 2 để tìm ra ẩn ban đầu

          - B5: Đối chiếu nghiệm tìm được với điều kiện sau đó kết luận

Ví dụ: Giải phương trình 

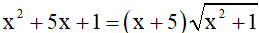 (1)

Giải

Đặt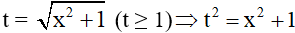

Phương trình (1) trở thành : 

t² + 5x = (x + 5)t

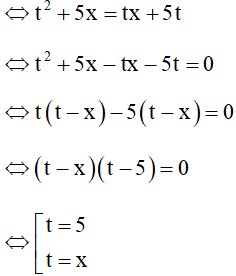
Với t = 5 (thỏa mãn) thì

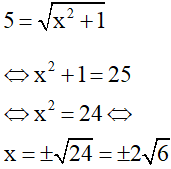
Với t = x thì

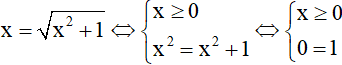
⇒vô nghiệm

Vậy phương trình có 2 nghiệm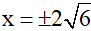

Dạng 3: Giải phương trình bằng cách đưa về hệ phương trình (hệ tạm)

Phương pháp

Nếu phương trình có dạng 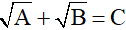 mà A – B = α.C ( C có thể là hằng số hoặc là biểu thức của x) thì ta có thể biến đổi  như sau

Phương trình

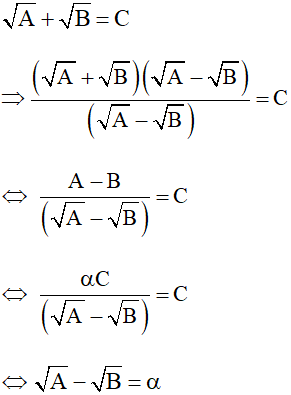
Khi đó ta có hệ phương trình

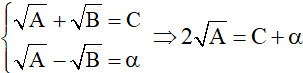
Ví dụ: Giải phương trình 

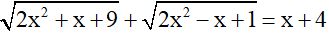(1)

Giải

Ta có

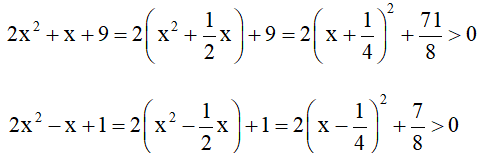
 ⇒phương trình luôn xác định với mọi x

Điều kiện phải thêm: VP = x + 4 ≥ 0 

Ta thấy

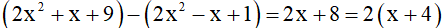
Với x = -4 thì (1) trở thành 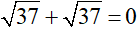 (vô lí) x = -4 không là nghiệm của phương trình (1)

Với x ≠ -4 thì nên ta nhân và chia VT(1) với biểu thức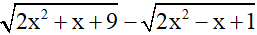

Phương trình 

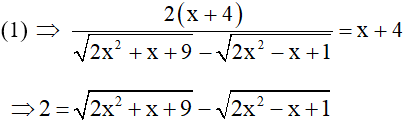
Khi đó ta có hệ

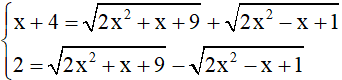
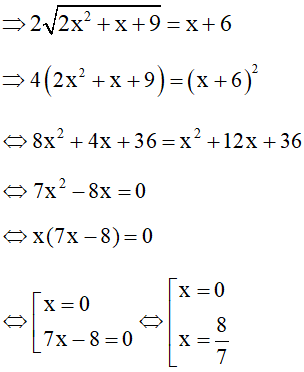
Ta thấy x = 0, x = 8/7 thỏa mãn x ≠ -4 và thử vào phương trình ban đầu là nghiệm của phương trình

Vậy phương trình có 2 nghiệm x = 0, x = 8/7

Dạng 4: Giải phương trình chứa ẩn ở mẫu

Phương pháp

Thực hiện các bước sau:

          Bước 1: Tìm điều kiện xác định của phương trình.

          Bước 2: Quy đồng mẫu thức hai vế rồi khử mẫu thức.

          Bước 3: Giải phương trình vừa nhận được.

          Bước 4: Trong các giá trị tìm được của ẩn, loại các giá trị không thoả mãn điều kiện xác định, các giá trị thoả mãn điều kiện xác định là nghiệm của phương trình đã cho.

Ví dụ 1: Giải phương trình: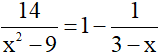                                  

Giải

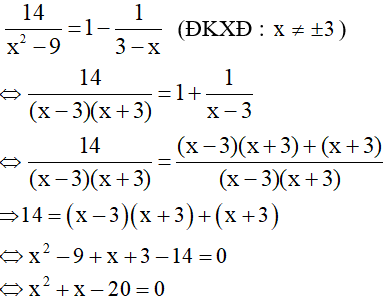
Ta có:

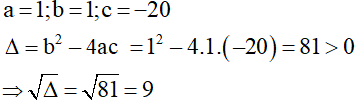
Phương trình có 2 nghiệm có 2 nghiệm phân biệt :

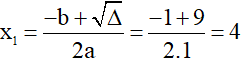
 (thỏa mãn điều kiện)

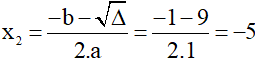
(thỏa mãn điều kiện)

Vậy phương trình đã cho có 2 nghiệm: x₁ = 4, x₂ = -5

Ví dụ 2 : Giải phương trình

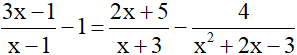 (1)

Giải

Phương trình 

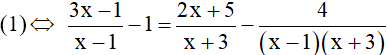
Điều kiện : x ≠ -3 và x ≠ 1

Phương trình

Ta thấy x = -3 không thỏa mãn điều kiện.

 Vậy phương trình vô nghiệm 

Dạng 5: Giải phương trình chứa dấu giá trị tuyệt đối

Phương pháp

Để giải phương trình chứa ẩn trong dấu giá trị tuyệt đối ta tìm cách khử dấu giá trị tuyệt đối bằng cách:

          + Dùng định nghĩa hoặc tính chất của dấu giá tri tuyệt đối 

                   

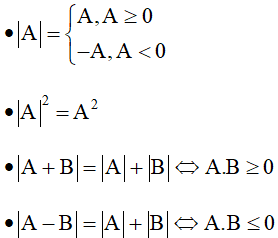
          + Bình phương hai vế của phương trình

          + Đặt ẩn phụ 

Một số dạng phương trình cơ bản

          + Dạng 1:

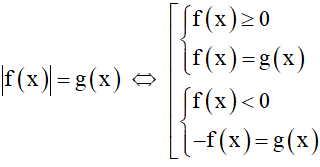
          + Dạng 2:

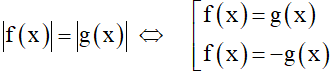
          + Dạng 3: 

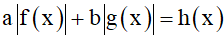
          Để giải phương trình này ta thường dùng phương pháp khoảng

Ví dụ: Giải các phương trình sau

       

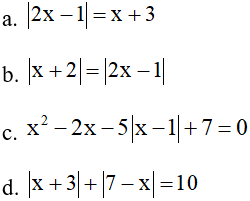
Giải

a. Phương trình

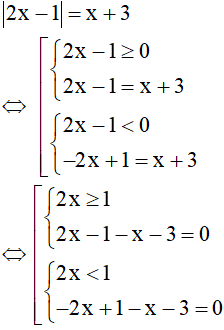
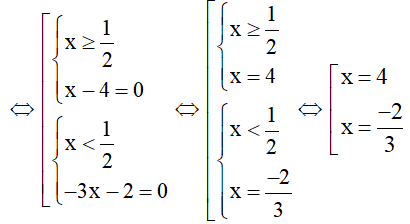
Vậy phương trình có 2 nghiệm x = 4, x = -2/3

b. Phương trình

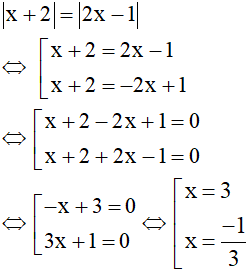
Vậy phương trình có 2 nghiệm x = 3, x = -1/3

c. Phương trình

Đặt 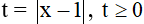. Khi đó phương trình trở thành  

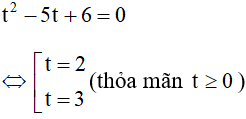
Với

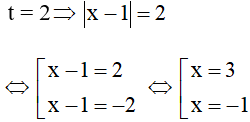
Với 

Vậy phương trình có 4 nghiệm x = 3, x = -1, x = 4, x = -2

d. Sử dụng định nghĩa dấu giá trị tuyệt đối ta có bảng phá dấu giá trị tuyệt đối sau

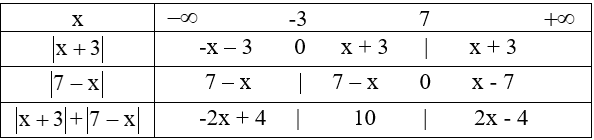
VVới x < -3 thì phương trình đã cho trở thành  -2x + 4 =10 -2x = 6x = -3

Ta thấy x = -3 không thỏa mãn điều kiện x < -3 (loại)

Với -3 ≤ x ≤ 7 thì phương trình đã cho trở thành  10 = 10 phương trình có vô số nghiệm thỏa mãn -3 ≤ x ≤ 7

Với x > 7 thì phương trình đã cho trở thành  2x - 4 =10 2x = 14x = 7

Ta thấy x = 7 không thỏa mãn điều kiện  x > 7 (loại)

Vậy tập nghiệm của phương trình là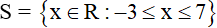

Bài tập áp dụng

Bài 1: Giải các phương trình sau

                                   

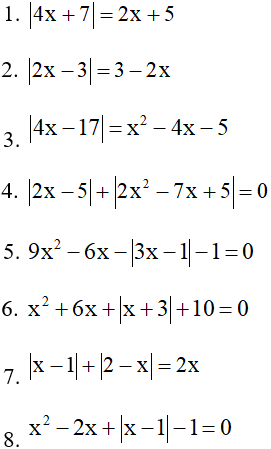
Bài 2: Giải các phương trình sau

     

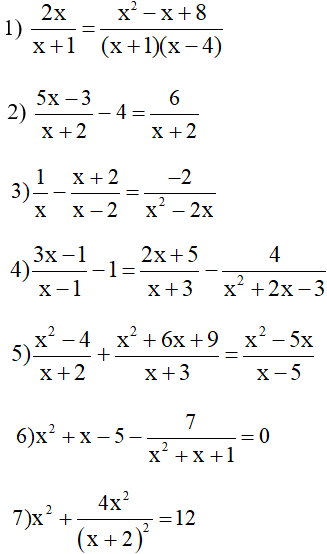
Bài 3 : Giải phương trình sau

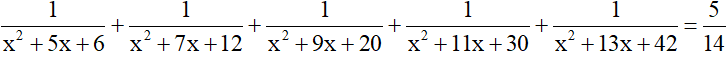
Bài 4: Giải các phương trình sau

         

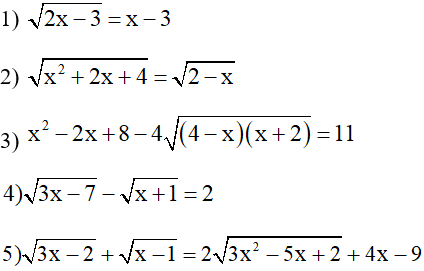
Bài 5: Giải phương trình  

1. (x - 1)⁴ + (x – 7)⁴ = 0

2. (x - 6)⁴ + (x – 2)⁴ = -224

3. (x +1)(x + 3)(x + 6)(x + 4) = -8

4. (x +5)(x + 4)(x - 1)(x - 2) = 112

Bài 6: Giải phương trình 

       

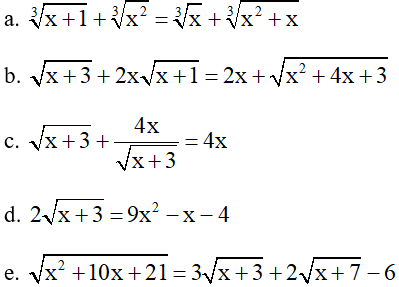
Bài 7: Giải phương trình

     

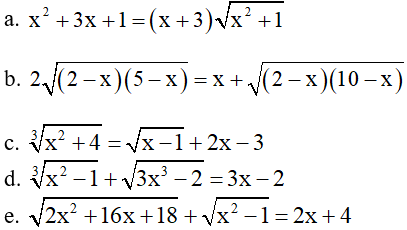
Bài 8: Giải phương trình

         

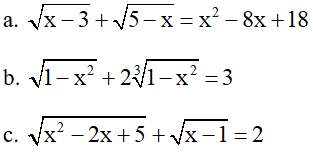
Xem thử Đề ôn vào 10 Xem thử Đề vào 10 Hà Nội Xem thử Đề vào 10 TP.HCM Xem thử Đề vào 10 Đà Nẵng

Xem thêm bộ tài liệu các dạng bài tập ôn thi vào lớp 10 môn Toán chọn lọc, hay khác:

• Các dạng bài Rút gọn biểu thức (ôn thi vào lớp 10 Toán 2024)
• Các dạng bài Giải hệ phương trình (ôn thi vào lớp 10 Toán 2024)
• Các dạng bài Giải bất phương trình (ôn thi vào lớp 10 Toán 2024)
• Các dạng bài Đồ thị hàm số (ôn thi vào lớp 10 Toán 2024)
• Các dạng bài Phương trình chứa tham số (ôn thi vào lớp 10 Toán 2024)

---