Phương pháp giải bài tập Quy tắc cộng xác suất (cực hay có lời giải)

Bài viết Phương pháp giải bài tập Quy tắc cộng xác suất với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập Phương pháp giải bài tập Quy tắc cộng xác suất.

Phương pháp giải bài tập Quy tắc cộng xác suất (cực hay có lời giải)

A. Phương pháp giải

+ Biến cố hợp: Cho hai biến cố A và B. Biến cố “ A hoặc B xảy ra”, kí hiệu là A∪B, được gọi là hợp của hai biến cố A và B.

+ Biến cố xung khắc: Cho hai biến cố A và B. Hai biến cố A và B được gọi là xung khắc nếu biến cố này xảy ra thì biến cố kia không xảy ra.

+ Quy tắc cộng xác suất: Nếu hai biến cố A và B xung khắc thì xác suất để A hoặc B xảy ra là: P(A∪B)=P(A)+P(B).

+ Mở rộng: Cho k biến cố A₁; A₂; ...; A_k đôi một xung khắc. Khi đó: P(A₁∪A₂∪…∪A_k )=P(A₁ )+P(A₂ )+⋯+P(A_k )

+ Mở rộng: Cho hai biến cố A và B ta có: P(A∪B)=P(A)+P(B)-P(A∩B)

B. Ví dụ minh họa

Ví dụ 1: Trường THPT A có 270 học sinh khối 10; 300 học sinh khối 11 và 280 học sinh khối 12. Nhà trường chọn 1 học sinh bất kì. Tính xác suất để học sinh đó không phải là học sinh khối 12.

A.28/85    B.57/85    C.55/85    D.Đáp án khác

Hướng dẫn giải :

Đáp án : B

+ Trường THPT A có tất cả: 270+ 300+ 280= 850 học sinh.

+ Gọi A là biến cố chọn được 1 học sinh khối 10.

B là biến cố chọn được 1 học sinh khối 11.

⇒ A∪B là học sinh được chọn không phải là khối 12.

Ta có: P(A)= 270/(850 )= 27/85 và P(B)= 300/850= 30/85

Do hai biến cố A và B xung khắc nên ta có:

P(A∪B)= P(A) + P(B)= 27/85+ 30/85= 57/85

Ví dụ 2: Bạn Mạnh có 10 bông hoa hồng; 8 bông hoa lan và 9 bông hoa ly. Bạn Mạnh định chọn 7 bông hoa để đi tặng bạn. Tính xác suất để 7 bông hoa đó cùng loại.

A.143/444015     B.82/444015     C.254/444015     D.186/444015

Hướng dẫn giải :

Đáp án : C

+ Gọi A là biến cố bạn Mạnh chọn 7 bông hoa hồng.

+ Gọi B là biến cố bạn Mạnh chọn 7 bông hoa lan.

+ Gọi C là biến cố bạn Mạnh chọn 7 bông hoa ly.

⇒ A∪B∪C: bạn Mạnh chọn 7 bông hoa cùng loại.

Các biến cô A; B; C đôi một xung khắc.

+ Số phần tử của không gian mẫu là:

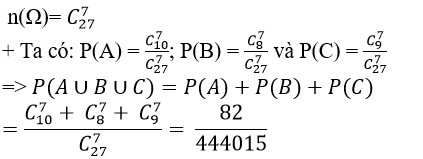
Ví dụ 3: Rút ra một lá bài từ bộ bài 52 lá. Xác suất để được lá cơ hoặc lá rô là

A.1/2    B.(1)/13    C.2/13    D.4/13

Hướng dẫn giải :

Đáp án : A

+ Gọi A là biến cố rút được lá cơ.

Và B là biến cố rút được lá rô.

Khi đó; A∪B: là biến cố rút được lá cơ hoặc lá rô.

+ Bộ bài có 52 lá; trong đó có 13 lá cơ và 13 lá rô.

⇒ Xác suất của hai biến cố A và B là:

P(A) = 13/52 = 1/4;P(B) = 13/52 = 1/4

+ Hai biến cố A và B xung khắc với nhau nên ta có:

P(A∪B)=P(A)+P(B) = 1/4+ 1/4 = 1/2

Ví dụ 4: Chọn ngẫu nhiên một vé xổ số có 5 chữ số được lập từ các chữ số từ 0 đến 9. Tính xác suất của biến cố X: “lấy được vé không có chữ số 2 hoặc chữ số 6 ”

A.0,8533

B.0,8535

C.0,8545

D.0,833

Hướng dẫn giải :

Đáp án : A

+ Số phần tử của không gian mẫu là: n(Ω)= 10⁵

Gọi A: “lấy được vé không có chữ số 2”

Gọi B: “lấy được vé số không có chữ số 6”

Suy ra n(A)=n(B)= 9⁵

P(A)=P(B)=9⁵/10⁵=()0,9)⁵

+ Số vé số trên đó không có chữ số 2 và 6 là: 8⁵, suy ra n(A∩B)= 8⁵

⇒ P(A∩B)= 8⁵/10⁵ = 0,8⁵

+ Ta có: X= A∪B nên P(X)=P(A)+P(B)-P(A∩B)= 0,8533.

Ví dụ 5: Gieo một con súc sắc đồng chất. Tính xác suất để xuất hiện mặt 1 chấm hoặc 6 chấm?

A.1/6    B.1/3     C.2/3    D.1/9

Hướng dẫn giải :

Đáp án : B

Gọi A là biến cố con súc sắc xuất hiện mặt 1 chấm.

B là biến cố con súc sắc xuất hiện mặt 6 chấm.

⇒ A∪B: Con súc sắc xuất hiện mặt 1 chấm hoặc 6 chấm.

Ta có: P(A)= 1/6;P(B)= 1/6

⇒ P (A∪B)=P(A)+P(B)= 1/6 + 1/6 = 1/3

Ví dụ 6: Một chiếc hộp có 8 thẻ đánh số từ 1 đến 8.Rút ngẫu nhiên hai thẻ rồi nhân hai số ghi trên hai thẻ với nhau. Tính xác suất để kết quả nhận được là một số chẵn ?

A.1/2    B.11/14    C.9/14    D.11/28

Hướng dẫn giải :

Đáp án : B

Kết qủa nhận được là số chẵn khi và chỉ khi trong hai thẻ có ít nhất một thẻ chẵn.

+ Gọi A là biến cố “ rút được 1 thẻ chẵn và 1 thẻ lẻ”

+ Gọi B là biến cố “ rút được 2 thẻ chẵn”.

⇒ A∪ B: Tích hai số ghi trên hai thẻ là 1 số chẵn.

Ta có 4 thẻ chẵn và 4 thẻ lẻ nên:

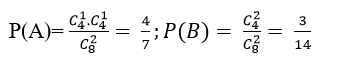
Hai biến cố A và B xung khắc với nhau nên:

P(A∪B)=P(A)+P(B)=4/7+ 3/14= 11/14

Ví dụ 7: Một tổ học sinh gồm có 6 nam và 4 nữ. Chọn ngẫu nhiên 3 em. Tính xác suất 3 em được chọn có ít nhất 1 nữ?

A.5/6    B.1/6    C.1/30    D.1/2

Hướng dẫn giải :

Đáp án : A

+ Gọi A là biến cố chọn ra 1 nữ và 2 nam.

Gọi B là biến cố chọn ra 2 nữ và 1 nam

Gọi C là biến cố chọn 3 nữ, 0 nam

⇒A∪B∪C: chọn được 3 em có ít nhất có 1 nữ.

+ Số phần tử cuả không gian mẫu là:

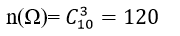
+ ta có:

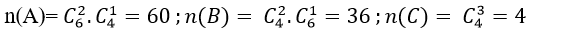
⇒ P(A) = 60/120= 1/2; P(B)= 36/120= 3/10 và P(C)= 4/120= 1/30

Do các biến cố A; B và C đôi một xung khắc nên áp dụng quy tắc cộng xác suất ta có:

P(A∪B∪C)=P(A)+P(B)+P(C)= 1/2+ 3/10+ 1/30= 5/6

Ví dụ 8: Trong một hộp đựng 6 bi xanh, 5 bi đỏ và 4 bi vàng. Lấy ngẫu nhiên 3 viên bi. Tính xác suất để 3 bi lấy ra cùng màu

A.17/455    B.34/455    C.68/455    D.134/455

Hướng dẫn giải :

Đáp án : B

+ Số phần tử của không gian mẫu là:

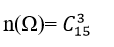
+ Gọi A là biến cố lấy ra 3 viên bi cùng màu xanh.

Gọi B là biến cố lấy ra 3 viên bi cùng màu đỏ.

Gọi C là biến cố lấy ra 3 viên bi cùng màu vàng.

⇒ A∪B∪C: Lấy ra 3 viên bi cùng màu.

+ Số kết quả thuận lợi cho A; B; C lần lượt là:

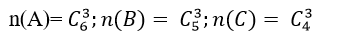
Xác suất của 3 biến cố A; B; C là:

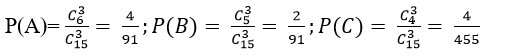
Xác suất cần tìm là:

P(A∪B∪C)=P(A)+P(B)+P(C)= 4/91+ 2/91+ 4/455= 34/455

C. Bài tập trắc nghiệm

Câu 1: Bộ bài lơ khơ có 52 lá bài. Rút ngẫu nhiên một lá bài.Tính xác suất để lá rút ra là lá át hoặc lá 8?

A.2/13     B.1/13     C.1/4    D.1/2

Lời giải:

Đáp án : A

+ Gọi A là biến cố lá rút ra là át.

Gọi B là biến cố lá rút ra là 8.

⇒ A∪B là biến cố lá rút ra là át hoặc 8.

+ Một bộ bài có 52 lá; trong đó có 4 lá át; 4 lá 8.

Xác suất của hai biến cố A và B là:

P(A) = 4/52 = 1/13;P(B) = 4/52 = 1/13

+ Vì hai biến cố A và B xung khắc với nhau nên ta có:

P(A∪B)=P(A)+P(B) = 1/13 + 1/13 = 2/13

Câu 2: Một con súc sắc không đồng chất sao cho mặt bốn chấm xuất hiện nhiều gấp 3 lần mặt khác, các mặt còn lại đồng khả năng. Tìm xác suất để xuất hiện một mặt chẵn

A.5/8    B.3/8    C.7/8     D.1/8

Lời giải:

Đáp án : A

Gọi A_i là biến cố xuất hiện mặt i chấm ( i=1;2;3;4;5;6)

Ta có: P(A₁)=P(A₂)= P(A₃)= P(A₅)= P(A₆)= 1/3 P(A₄)= x

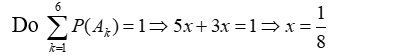
Gọi A là biến cố xuất hiện mặt chẵn, suy ra A= A₂∪A₄∪A₆

Vì cá biến cố A_i xung khắc nên:

P(A)= P(A₂)+ P(A₄)+ P(A₆)= 1/8+ 3/8+ 1/8 = 5/8.

Câu 3: Một bài trắc nghiệm có 10 câu hỏi, mỗi câu hỏi có 4 phương án lựa chọn trong đó có 1 đáp án đúng. Giả sử mỗi câu trả lời đúng được 5 điểm và mỗi câu trả lời sai bị trừ đi 2 điểm. Một học sinh không học bài nên đánh hú họa một câu trả lời. Tìm xác suất để học sinh này nhận điểm dưới 1.

A.0,7124    B.0,7759    C.0,7336    D.0,783

Lời giải:

Đáp án : B

Ta có xác suất để học sinh trả lời câu đúng là 1/4 và xác suất trả lời câu sai là 3/4.

Gọi x là số câu trả lời đúng, khi đó số câu trả lời sai là 10- x

Số điểm học sinh này đạt được là : 4x – 2( 10- x) = 6x- 20

Nên học sinh này nhận điểm dưới 1 khi 6x- 20 <1 ⇔ x<21/6

Mà x nguyên nên x nhận các giá trị: 0,1,2,3

Gọi Ai ( i= 0,1,2,3) là biến cố: “Học sinh trả lời đúng i câu”

A là biến cố: “ Học sinh nhận điểm dưới 1”

Suy ra

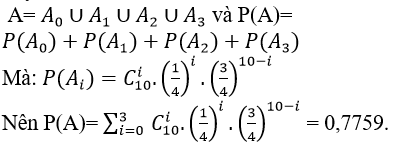
Câu 4: Một hộp đựng 4 viên bi xanh, 3 viên bi đỏ và 2 viên bi vàng. Chọn ngẫu nhiên hai viên biên. Xác suất để chọn được hai viên bi cùng màu là

A.5/18    B.1/6    C.5/12    D.1/36

Lời giải:

Đáp án : A

Gọi A là biến cố : “Chọn được hai viên bi xanh”.

Gọi B là biến cố : “Chọn được hai viên bi đỏ”.

Gọi C là biến cố : “Chọn được hai viên bi vàng”.

Khi đó biến cố: “Chọn được hai viên bi cùng màu” là biến cố A∪B∪C. Do A; B; C đôi một xung khắc với nhau nên theo quy tắc cộng ta có

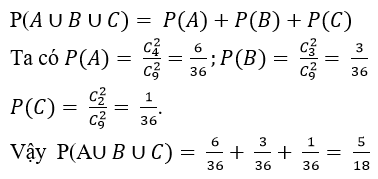
Câu 5: Trong một hộp đựng 7 bi xanh, 5 bi đỏ và 3 bi vàng. Lấy ngẫu nhiên 3 viên bi, tính xác suất để được ít nhất 2 bi vàng được lấy ra.

A.37/455    B.22/455    C.10/91    D.144/455

Lời giải:

Đáp án : A

+ Số phần tử của không gian mẫu là:

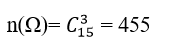
+ Gọi A là biến cố lấy được 2 bi vàng; 1 bi đỏ

Gọi B là biến cố lấy được 2 bi vàng; 1 bi xanh.

Gọi C là biến cố lấy được 3 bi vàng

⇒ A∪B∪C trong 3 bi lấy ra có ít nhất 2 bi vàng.

Số kết quả thuận lợi cho biến cố A; B và C lần lượt là:

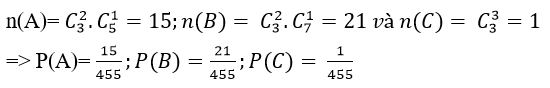
Do ba biến cố A; B và C đôi một xung khắc nên theoquy tắc cộng xác suất ta có:

P(A∪B∪C)=P(A)+P(B)+P(C) = 15/455 + 21/455 + 1/455 = 37/455

Câu 6: Trong bộ môn Toán, thầy giáo có 40 câu hỏi khác nhau gồm 5 câu hỏi khó, 15 câu trung bình, 20 câu hỏi dễ. Một ngân hàng đề thi mỗi đề thi có 7 câu hỏi được chọn từ 40 câu hỏi đó. Tính xác suất để chọn được đề thi từ ngân hàng đề nói trên nhất thiết phải có đủ 3 loại câu hỏi (khó, trung bình, dễ) và số câu hỏi dễ không ít hơn 4.

A.183/3848    B.2745/3848    C.915/3848    D.1830/3848

Lời giải:

Đáp án : C

+ Gọi X là biến cố đề thi có 7 câu hỏi được chọn đủ 3 loại và số câu dễ không ít hơn 4.

+ Số phần tử của không gian mẫu:

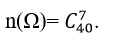
Do đủ 3 loại mà số câu dễ không ít hơn 4 nên số câu dễ chỉ có thể là 4 hoặc 5.

+ Gọi A là biến cố đề thi có 5 câu dễ; 1 câu trung bình; 1 câu khó.

Gọi B là biến cố đề thi có 4 câu dễ; 2 câu trung bình và 1 câu khó.

Gọi C là biến cố đề thi có 4 câu dễ; 1 câu trung bình và 2 câu khó.

⇒ X= A∪B∪C và các biến cố A; B; C đôi một xung khắc.

+ Ta tính số kết quả thuận lợi cho các biến cố:

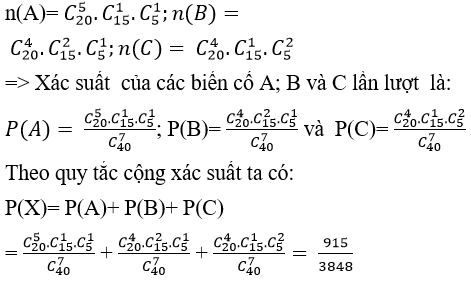
Câu 7: Đội dự tuyển học sinh giỏi giải toán trên máy tính cầm tay môn toán của một trường phổ thông có 4 học sinh nam khối 12, 2 học sinh nữ khối 12 và 2 học sinh nam khối 11. Để thành lập đội tuyển dự thi học sinh giỏi giải toán trên máy tính cầm tay môn toán cấp tỉnh nhà trường cần chọn 5 em từ 8 em học sinh trên. Tính xác suất để trong 5 em được chọn có cả học sinh nam và học sinh nữ, có cả học sinh khối 11 và học sinh12.

A.2/5    B.5/14    C.11/14    D.2/7

Lời giải:

Đáp án : C

Gọi X là biến cố trong 5 em được chọn có cả học sinh nam và học sinh nữ, có cả học sinh khối 11 và 12.

+ Số phần tử không gian mẫu:

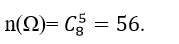
+ Gọi A là biến cố chọn được 2 nam 11; 1 nữ 12 và 2 nam 12.

+ Gọi B là biến cố chọn được 2 nam 11; 2 nữ 12 và 1 nam 12.

+ Gọi C là biến cố chọn được 1 nam 11; 1 nữ 12; 3 nam 12.

+ Gọi D là biến cố chọn được 1 nam 11; 2 nữ 12; 2 nam 12.

⇒ X= A∪B∪C∪D và các biến cố A; B; C, D đôi một xung khắc.

+ Ta tính số kết quả thuận lợi cho các biến cố là

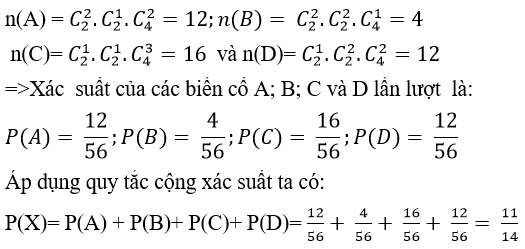
Câu 8: Trường trung học phổ thông T có tổ Toán gồm 15 giáo viên trong đó có 8 giáo viên nam, 7 giáo viên nữ. Tổ Lý gồm 12 giáo viên trong đó có 5 giáo viên nam, 7 giáo viên nữ. Chọn ngẫu nhiên mỗi tổ 2 giáo viên đi dự tập huấn chuyên đề dạy học tích hợp. Tính xác suất sao cho trong các giáo viên được chọn có 2 nam và 2 nữ.

A.291/495    B.197/495    C.394/495    D.253/495

Lời giải:

Đáp án : B

+ Gọi X là biến cố trong các giáo viên được chọn có 2 nam và 2 nữ.

Số phần tử của không gian mẫu:

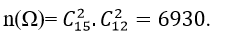
+ Gọi A là biến cố chọn được 2 nam toán; 2 nữ lý.

B là biến cố chọn được 2 nữ toán và 2 nam lý.

C là biến cố 1 nam toán; 1 nam lý; 1 nữ toán; 1 nữ lý

=> X=A∪B∪C và các biến cố A; B; C đôi một xung khắc.

+ Ta tính số kết quả thuận lợi cho các biến cố:

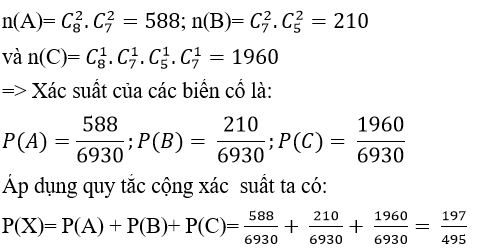
Câu 9: Trong kì thi học sinh giỏi cấp tỉnh của trường THPT Hùng Vương có 10 học sinh đạt giải trong đó có 4 học sinh nam và 6 học sinh nữ. Nhà trường muốn chọn một nhóm 5 học sinh trong 10 học sinh trên để tham dự buổi lễ tuyên dương khen thưởng cuối học kỳ 1 do huyện tổ chức. Tính xác suất để chọn được một nhóm gồm 5 học sinh mà có cả nam và nữ, biết số học sinh nam ít hơn số học sinh nữ

A.5/7    B.2/3    C.4/3    D.1/4

Lời giải:

Đáp án : A

+ Số phần tử của không gian mẫu là:

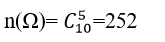
+ Gọi A là biến cố chọn được 4 nữ và 1 nam.

Gọi B là biến cố chọn được 3 nữ và 2 nam.

=> A∪B là biến cố có cả nam và nữ ; số học sinh nam ít hơn số học sinh nữ.

+ Ta tính số kết quả thuận lợi cho hai biến cố A và B :

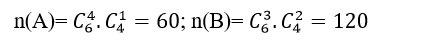
=> Xác suất của hai biến cố A và B là:

P(A)= 60/252;P(B)=120/252

Hai biến cố A và B xung khắc với nhau; áp dụng quy tắc cộng xác suất ta có:

P(A∪B) = P(A)+P(B) = 60/252 + 120/252 = 5/7

D. Bài tập tự luyện

Bài 1. Một hộp đựng 6 viên bi màu trắng và 8 viên bi màu đỏ, có cùng kích thước và khối lượng. Bạn Sơn lấy ngẫu nhiên một viên bi từ hộp (lấy xong không trả lại vào hộp). Tiếp đó đến lượt bạn Tùng lấy ngẫu nhiên một viên bi từ hộp đó. Tính xác suất để bạn Tùng lấy được viên bi màu trắng.

Bài 2. Ba xạ thủ cùng bắn súng vào một bia độc lập nhau. Xác suất bắn trúng bia của xạ thủ thứ nhất, thứ hai, thứ ba tương ứng là 0,7; 0,8 và 0,9. Tính xác suất để:

(a) Có duy nhất một xạ thủ bắn trúng bia;

(b) Có đúng hai xạ thủ bắn trúng bia;

(c) Có ít nhất một xạ thủ bắn trúng bia;

(d) Xạ thủ thứ nhất bắn trúng bia biết rằng có hai xạ thủ bắn trúng bia.

Bài 3. Một lớp có 100 sinh viên, trong đó có 40 sinh viên giỏi ngoại ngữ, 30 sinh viên giỏi toán, 20 sinh viên vừa giỏi ngoại ngữ, vừa giỏi toán. Chọn ngẫu nhiên một sinh viên trong lớp. Tìm xác suất để sinh viên đó giỏi ít nhất một trong hai môn trên.

Bài 4. Một lớp có 50 sinh viên, trong đó có 20 sinh viên học giỏi Toán; 30 sinh viên học giỏi Anh văn; 10 sinh viên học giỏi cả hai môn Toán và Anh văn. Chọn ngẫu nhiên một sinh viên của lớp. Tun xác suất để chọn được sinh viên học giỏi ít nhất một môn trong hai môn Toán và Anh văn.

Bài 5. Một hộp có 10 sản phẩm (trong đó có 2 phế phẩm). Lấy ngẫu nhiên không hoàn lại từ hộp ra 6 sản phẩm. Tìm xác suất để có không quá 1 phế phẩm trong 6 sản phẩm lấy ra.

Xem thêm các dạng bài tập Toán lớp 11 có trong đề thi THPT Quốc gia khác:

• Cách tìm xác suất của biến cố (cực hay có lời giải)
• Cách tính xác suất bài toán liên quan đến đếm số (cực hay có lời giải)
• Cách tính xác suất bài toán liên quan đến hình học (cực hay có lời giải)
• Cách giải bài tập Xác suất nâng cao, (cực hay có lời giải)
• Phương pháp giải bài tập Biến cố đối (cực hay có lời giải)
• Phương pháp giải bài tập Quy tắc nhân xác suất (cực hay có lời giải)

---