Phương pháp giải bài tập Quy tắc nhân xác suất (cực hay có lời giải)

Bài viết Phương pháp giải bài tập Quy tắc nhân xác suất với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập Phương pháp giải bài tập Quy tắc nhân xác suất.

Phương pháp giải bài tập Quy tắc nhân xác suất (cực hay có lời giải)

A. Phương pháp giải

+ Biến cố giao: Cho hai biến cố A và B. Biến cố “ cả A và B cùng xảy ra”, kí hiệu là AB, được gọi là giao của hai biến cố A và B.

+ Biến cố độc lập:Hai biến cố A và B được gọi là độc lập với nhau nếu việc xảy ra hay không xảy ra của biến cố này không làm ảnh hưởng tới xác suất xảy ra của biến cố kia.

+ Quy tắc nhân xác suất: Nếu hai biến cố A và B độc lập với nhau thì P(AB)= P(A).P(B)

+ Mở rộng: Nếu k biến cố A₁; A₂; ..; A_k độc lập với nhau thì :

P(A₁A₂..A_k)= P(A₁).P(A₂)...P(A_k)

B. Ví dụ minh họa

Ví dụ 1: Một bình đựng 9 viên bi xanh và 7 viên bi đỏ. Lần lượt lấy ngẫu nhiên ra 2 bi, mỗi lần lấy 1 bi. Tính xác suất để bi thứ 2 màu xanh nếu biết bi thứ nhất màu đỏ?

A.9/17    B.21/80    C.63/256     D.9/16

Hướng dẫn giải :

Đáp án : B

Gọi A là biến cố lần thứ nhất lấy được bi màu đỏ.

Gọi B là biến cố lần thứ hai lấy được bi màu xanh.

Xác suất để lần thứ nhất lấy được bi màu đỏ là: P(A)= 7/16

Xác suất để lần thứ hai lấy được bi màu xanh (trong 15 viên bi còn lại) là: P(B)= 9/15= 3/5.

Hai biến cố A và B độc lập với nhau nên áp dụng quy tắc nhân xác suất ta có:

P(AB)= P(A). P(B)=7/16.3/5 = 21/80

Ví dụ 2: Một bình đựng 7 viên bi trắng và 5 viên bi đen. Lần lượt lấy ngẫu nhiên ra 2 bi. Tính xác suất để lấy được bi thứ 1 màu trắng và bi thứ 2 màu đen?

A.1/35    B.35/144    C.35/132    D.Đáp án khác

Hướng dẫn giải :

Đáp án : C

Gọi A là biến cố lần thứ nhất lấy được bi màu trắng.

Gọi B là biến cố lần thứ hai lấy được bi màu đen.

⇒ AB là biến cố lần thứ nhất lấy được bi màu trắng; lần thứ hai lấy được bi màu đen. Ta thấy 2 biến cố A và B độc lập với nhau.

Xác suất để lần thứ nhất lấy được bi màu trắng là: P(A) = 7/12.

Xác suất để lần thứ hai lấy được bi màu đen (trong 11 viên bi còn lại) là P(B)= 5/11.

Áp dụng quy tắc nhân xác suất; xác suất cần tìm là:

P(AB) = P(A).P(B)= 7/12.5/11 = 35/132

Ví dụ 3: Một bộ bài tú lơ khơ có 52 con, rút ngẫu nhiên lần lượt 3 con, mỗi lần 1 con. Xác suất để hai lần đầu rút được con Át và lần thứ ba rút được con J là

A.2/13    B.2/5525    C.3/13    D.3/8788

Hướng dẫn giải :

Đáp án : B

+ Gọi A là biến cố lần thứ nhất rút được con Át

Gọi B là biến cố lần thứ hai rút được con Át.

Gọi C là biến cố lần thứ ba rút được con J.

⇒ ABC là biến cố hai lần đầu rút được con Át và lần thứ ba rút được con J. Các biến cố A; B và C đôi một độc lập với nhau.

+ Xác suất rút con thứ nhất là con Át là P(A)= 4/52 = 1/13.

Xác suất rút con thứ hai là con Át (rút con Át trong 51 con còn lại) là P(B) = 3/51 = 1/17.

Xác suất rút con thứ ba là con J là P(C) = 4/50 = 2/25.

Vậy xác suấ cần tính là : P(ABC)= P(A). P(B). P(C)= 1/13. 1/17. 2/25 = 2/5525

Ví dụ 4: Cho ba hộp giống nhau, mỗi hộp 7 bút chỉ khác nhau về màu sắc

Hộp thứ nhất : Có 3 bút màu đỏ, 2 bút màu xanh, 2 bút màu đen

Hộp thứ hai : Có 2 bút màu đỏ, 2 màu xanh, 3 màu đen

Hộp thứ ba : Có 5 bút màu đỏ, 1 bút màu xanh, 1 bút màu đen

Lấy ngẫu nhiên một hộp, rút từ hộp đó ra 2 bút. Tính xác suất của biến cố A: “Lấy được hai bút màu xanh”

A.1/63    B.2/63    C.0,235    D.31/63

Hướng dẫn giải :

Đáp án : B

Gọi X_i là biến cố rút được hộp thứ i, i=1;2;3 ⇔ P(X_i) = 1/3

Gọi A_i là biến cố lấy được hai bút màu xanh ở hộp thứ i, i=1;2;3

Ta có:

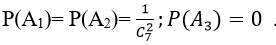
Do A=A₁∪A₂∪A₃ và các A_i xung khắc với nhau vậy

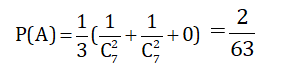
Ví dụ 5: Hai người độc lập nhau ném bóng vào rổ. Mỗi người ném vào rổ của mình một quả bóng. Biết rằng xác suất ném bóng trúng vào rổ của từng người tương ứng là 1/3 và 3/7. Gọi A là biến cố: “Cả hai cùng ném bóng trúng vào rổ”. Khi đó, xác suất của biến cố A là bao nhiêu?

A.12/35    B.1/5    C.16/21    D.1/7

Hướng dẫn giải :

Đáp án : D

Gọi A là biến cố: “Cả hai cùng ném bóng trúng vào rổ. “

Gọi X là biến cố: “người thứ nhất ném trúng rổ. Theo giả thiết P(X)= 1/3

Gọi Y là biến cố: “người thứ hai ném trúng rổ.Theo giả thiết P(Y)= 3/7

Ta thấy biến cố X, Y là 2 biến cố độc lập nhau, theo công thức nhân xác suất ta có:

P(A)= P(XY)= P(X). P(Y)= 1/3.3/7= 1/7

Ví dụ 6: Cho ba hộp giống nhau, mỗi hộp 7 bút chỉ khác nhau về màu sắc

Hộp thứ nhất : Có 3 bút màu đỏ, 2 bút màu xanh, 2 bút màu đen

Hộp thứ hai : Có 2 bút màu đỏ, 2 màu xanh, 3 màu đen

Hộp thứ ba : Có 5 bút màu đỏ, 1 bút màu xanh, 1 bút màu đen

Lấy ngẫu nhiên một hộp, rút từ hộp đó ra 2 bút.Tính xác suất của biến cố B: “Lấy được hai bút không có màu đen”

A.1/63     B.2/33     C.0,235    D.31/63

Hướng dẫn giải :

Đáp án : D

+ Gọi B_i là biến cố rút hai bút ở hộp thứ i không có màu đen.

Ta thấy các biến cố B1; B2; B3 đôi một xung khắc với nhau

+ Xác suất lấy được hộp thứ 1 là 1/3

Tương tự; xác suất để lấy được hộp thứ 2; thứ 3 cũng là 1/3

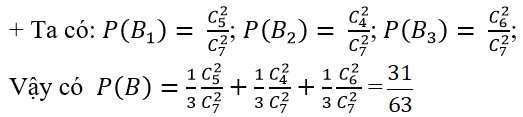
Ví dụ 7: Một chiếc máy có hai động cơ I và II hoạt động độc lập với nhau.Xác suất để động cơ I và động cơ II chạy tốt lần lượt là 0,8 và 0,9. Hãy tính xác suất để cả hai động cơ đều chạy tốt ;

A.0,81    B.0,64    C.0,17    D.0,72

Hướng dẫn giải :

Đáp án : D

Gọi A là biến cố "Động cơ I chạy tốt"

      B là biến cố "Động cơ II chạy tốt"

      C là biến cố "Cả hai động cơ đều chạy tốt".

Ta thấy A, B là hai biến cố độc lập với nhau và C=A.B

Áp dụng quy tắc nhân xác suất ta có:

P(C)=P(AB)=P(A).P(B)=0,8. 0,9=0,72

Ví dụ 8: Một chiếc máy có hai động cơ I và II hoạt động độc lập với nhau. Xác suất để hai động cơ I và II chạy tốt lần lượt là 0,7 và 0,9. Tính xác suất để cả hai động cơ đều không chạy tốt?

A.0,03 B.0,63 C.0,2 D.0,04

Hướng dẫn giải :

Đáp án : A

Gọi A là biến cố "Động cơ I chạy không tốt" ⇒ P(A)= 1- 0,7= 0,3

      B là biến cố "Động cơ II chạy không tốt" ⇒ P(B)= 1- 0,9= 0,1

      C là biến cố "Cả hai động cơ đều chạy không tốt".

Ta thấy A, B là hai biến cố độc lập với nhau và C=A.B

Áp dụng quy tắc nhân xác suất ta có:

P(C)= P(AB)= P(A). P(B)= 0,3. 0,1= 0,03

Ví dụ 9: Một chiếc máy có hai động cơ I và II hoạt động độc lập với nhau. Xác suất để hai động cơ I và II chạy tốt lần lượt là 0,8 và 0,7. Tính xác suất để có ít nhất một động cơ chạy tốt?

A.0,06    B.0,94    C.0,56    D.0,875

Hướng dẫn giải :

Đáp án : C

Gọi A là biến cố "Động cơ I chạy không tốt" ⇒ P(A)= 1- 0,8= 0,2

      B là biến cố "Động cơ II chạy không tốt" ⇒ P(B)= 1- 0,7= 0,3

      C là biến cố "Có ít nhất một động cơ chạy tốt".

⇒ Biến cố đối C: Cả hai động cơ chạy không tốt

Ta thấy A, B là hai biến cố độc lập với nhau và C=A.B

Áp dụng quy tắc nhân xác suất ta có:

P(C)= P(A).P(B)= 0,2 .0,3= 0 ,06

+ Do hai biến cố C và C đối nhau nên:

P(C)= 1- P(C)= 1- 0,06= 0,94

Ví dụ 10: Gieo một con xúc sắc cân đối và đồng chất 2 lần. Tính xác suất sao cho tổng số chấm trong hai lần gieo là số chẵn.

A.0,8    B.0,91    C.0,9    D.0,5

Hướng dẫn giải :

Đáp án : D

Gọi A là biến cố “ Lần gieo đầu tiên xuất hiện mặt chấm chẵn”;

      B là biến cố “ Lần gieo thứ hai xuất hiện mặt chấm chẵn”;

      C là biến cố “ Tổng số chấm trong hai lần gieo là số chẵn”.

⇒ C = (A.B)∪(A.B) .

Ta thấy (A.B) và (A.B) là hai biến cố xung khắc nên:

P(C) = P[(A.B)∪(A.B)]= P[ (A.B)]+P[(A.B)]

+ Vì A và B là hai biến cố độc lập; áp dụng quy tắc nhân xác suất ta có:

P(A.B)= P(A).P(B)= 1/2. 1/2= 1/4

Và P(A.B)=P(A ).P(B)= 1/2.1/2 = 1/4

Vậy P(C)= 1/4+ 1/4= 1/2

Ví dụ 11: Ba xạ thủ A; B và C độc lập với nhau cùng nổ súng vào một mục tiêu. Xác suất bắn trúng mục tiêu của A; B; C tương ứng là 0,5; 0,6 và 0,8. Tính xác suất để có ít nhất một người bắn trúng mục tiêu.

A.0,96    B.0,9    C.0,4    D.0, 84

Hướng dẫn giải :

Đáp án : A

Gọi A; B; C tương ứng là các biến cố “ A bắn trúng”; “ B bắn trúng”; “ C bắn trúng”.

⇒ A; B và C là ba biến cố độc lập.

Ta có: P(A)= 0,5; P(B) = 0,6; P(C)= 0,8

⇒ P(A)=0,5;P(B )=0,4;P(C )=0,2

Do A; B; C là các biến cố đôi một nên:

Xác suất để cả ba người đều bắn trượt là

P(ABC )=P(A ).P(B ).P(C ) = 0,5.0,4. 0,2= 0,04

Vậy xác suất để có ít nhất một trong ba người bắn trùng là

1- 0,04= 0, 96

C. Bài tập trắc nghiệm

Câu 1: Ba người cùng bắn vào 1 bia. Xác suất để người thứ nhất, thứ hai, thứ ba bắn trúng đích lần lượt là 0,8; 0,6; 0,5. Xác suất để có đúng 2 người bắn trúng đích bằng:

A.0,24    B.0,96    C.0,46    D.0,92

Lời giải:

Đáp án : C

Gọi X là biến cố: “có đúng 2 người bắn trúng đích”.

Gọi A là biến cố: “người thứ nhất bắn trúng đích

P(A) = 0,8; P(A)=0 ,2

Gọi B là biến cố: “người thứ hai bắn trúng đích

P(B)= 0,6 và P(B)=0,4

Gọi C là biến cố: “người thứ ba bắn trúng đích

P(C)= 0,5; P(C)= 0,5

Ta thấy biến cố A, B, C là 3 biến cố độc lập nhau, theo công thức nhân xác suất ta có:

P(X)=P(A.B.C)+P(A.B.C)+P(A.B.C) = 0,8.0,6.0.5+0,8.0,4.0,5+0,2.0,6.0,5=0,46

Câu 2: Có 10 xạ thủ trong đó có hai xạ thủ I và tám xạ thủ II. Xác suất bắn trúng của I là 0,9 ; xác suất của II là 0,8. Lấy ngẫu nhiên một trong mười xạ thủ, bắn một viên đạn.Tính xác suất để viên đạn bắn ra trúng đích.

A.0,64    B.0,84    C.0,78    D.0,82

Lời giải:

Đáp án : D

Gọi B_i là biến cố “Xạ thủ được chọn lọai i,i=1,2

A là biến cố viên đạn trúng đích.

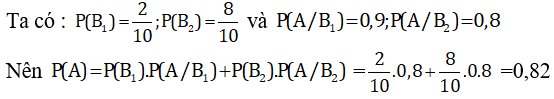
Câu 3: Một máy có 5 động cơ gồm 3 động cơ bên cánh trái và hai động cơ bên cánh phải. Mỗi động cơ bên cánh phải có xác suất bị hỏng là 0,09, mỗi động cơ bên cánh trái có xác suất bị hỏng là 0,04. Các động cơ hoạt động độc lập với nhau. Máy bay chỉ thực hiện được chuyến bay an toàn nếu có ít nhất hai động cơ làm việc. Xác suất để máy bay thực hiện được chuyến bay an toàn gần với giá trị nào nhất

A.0,9999    B.0,9814    C.0,9909    D.0,9141

Lời giải:

Đáp án : A

Gọi A là biến cố: “Máy bay bay an toàn”.

Khi đó A là biến cố: “Máy bay bay không an toàn”.

Ta có máy bay bay không an toàn khi xảy ra một trong các trường hợp sau

TH 1: Cả 5 động cơ đều bị hỏng

Ta có xác suất để xảy ra trường hợp này là: (0,09)³.(0,04)²

TH 2: Có một động cơ ở cánh phải hoạt động và các động cơ còn lại đều bị hỏng. Xác suất để xảy ra trường hợp này là: 3. (0,09)². 0,91.(0,04)²

TH 3: Có một động cơ bên cánh trái hoạt động, các động cơ còn lại bị hỏng

Xác suất xảy ra trường hợp này là: 2. 0,04. 0,96.(0,09)³

P(A)=(0,09)³.(0,04)²+3.(0,09)².0,91.(0,04)²+2.0,04.0,96.(0,09)³ = 0,925344.10^-4

Vậy P(A) = 1- P(A)= 0,9999074656.

Câu 4: Có 3 chiếc hộp. Hộp A chứa 3 bi đỏ, 5 bi trắng. Hộp B chứa 2 bi đỏ,2 bi vàng. Hộp C chứa 2 bi đỏ, 3 bi xanh. Lấy ngẫu nhiên một hộp rồi lấy một bi từ hộp đó. Xác suất để được một bi đỏ là:

A.1/8    B.1/6    C.2/15    D.17/40

Lời giải:

Đáp án : D

+ Lấy ngẫu nhiên một hộp

Gọi A là biến cố lấy được hộp A

Gọi B là biến cố lấy được hộp B

Gọi C là biến cố lấy được hộp C

Vậy P(A)=P(B)=P(C)=1/3

+ Gọi D là biến cố “ lấy ngẫu nhiên một hộp, trong hộp đó lại lấy ngẫu nhiên một viên bi và được bi đỏ ” là D=(D∩A)∪(D∩B)∪(D∩C)

Do đó :

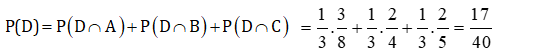
Câu 5: Ba cầu thủ sút phạt đến 11m, mỗi người đá một lần với xác suất làm bàn tương ứng là x;y và 0,6 (với x>y). Biết xác suất để ít nhất một trong ba cầu thủ ghi bàn là 0,976 và xác suất để cả ba cầu thủ đều ghi ban là 0,336. Tính xác suất để có đúng hai cầu thủ ghi bàn.

A.0,452    B.0,435    C.0,4525    D.0,4245

Lời giải:

Đáp án : A

Gọi Ai là biến cố “người thứ i ghi bàn” với i=1;2;3.

Ta có các Ai độc lập với nhau và P(A₁)= x; P(A₂)= y; P(A₃)= 0,6 .

Gọi A là biến cố: “ Có ít nhất một trong ba cầu thủ ghi bàn”

Gọi B: “ Cả ba cầu thủ đều ghi bàn”

Gọi C: “Có đúng hai cầu thủ ghi bàn”

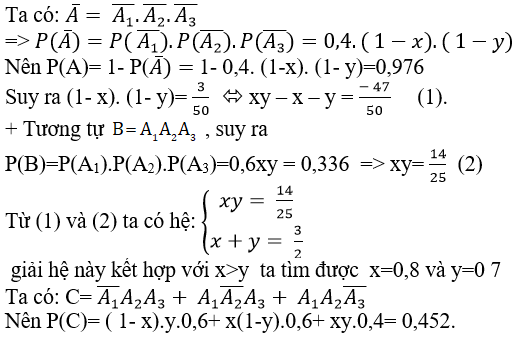
Câu 6: Ba người cùng bắn vào 1 bia. Xác suất để người thứ nhất, thứ hai, thứ ba bắn trúng đích lần lượt là 0,8; 0,6; 0,5. Xác suất để có đúng 2 người bắn trúng đích bằng:

A.0,24    B.0,96    C.0,46    D.0,92

Lời giải:

Đáp án : C

Gọi ba người cùng bắn vào 1 bia với xác suất 0,8; 0,6; 0,5 lần lượt là A, B, C.

TH1. A, B bắn trúng, C không bắn trúng nên xác suất là P₁= P_A.P_B.(1- P_C)= 0,24.

TH2. A, C bắn trúng, B không bắn trúng nên xác suất là P₂= P_A.( 1- P_B).P_C= 0,16.

TH3. B, C bắn trúng, A không bắn trúng nên xác suất là P₃= (1- P_A).P_B. P_C = 0,06.

Vậy xác suất cần tính là P= P₁+ P₂+ P₃ = 0,46.

Câu 7: Xác suất bắn trúng mục tiêu của một vận động viên khi bắn một viên đạn là 0,6. Người đó bắn hai viên một cách độc lập. Xác suất để một viên trúng và một viên trượt mục tiêu là:

A.0,24    B.0,45    C.0,4    D.0,48

Lời giải:

Đáp án : D

Xác suất người đó bắn trúng mục tiêu là 0,6. Nên xác suất người đó bắn trượt mục tiêu là: 1- 0,6= 0,4.

Một viên trúng và một viên trượt thì có thể là viên đầu tiên trúng, viên thứ hai trượt hoặc ngược lại.

Do đó xác suất cần tìm là: 0,6.0,4 + 0,4. 0,6 = 0,48

Câu 8: Gieo hai con súc sắc I và II cân đối, đồng chất một cách độc lập. Ta có biến cố A: “Có ít nhất một con súc sắc xuất hiện mặt chấm”. Lúc này giá trị của P(A) là

A.25/36    B.11/36    C.1/36    D.15/36

Lời giải:

Đáp án : B

+ Gọi A_i ( i= 1; 2) là biến cố : “Con súc sắc thứ i ra mặt 6 chấm”

⇒ A₁ và A₂ là hai biến cố độc lập và A= A₁.A₂

P(A₁)= 1/6;P(A₂)= 1/6

⇒ P(A₁)=1- 1/6= 5/6;P(A₂ )=1- 1/6 = 5/6

+ Ta tính P(A). Do A= A₁.A₂ và hai biến cố A₁; A₂ độc lập với nhau nên ta có:

P(A)=P( A₁).P( A₂) = 5/6.5/6 = 25/36

Vậy P(A) = 1- P(A )=1- 25/36= 11/36

Câu 9: Một chiếc ôtô với hai động cơ độc lập đang gặp trục trặc kĩ thuật. Xác suất để động cơ 1 gặp trục trặc là 0,3. Xác suất để động cơ 2 gặp trục trặc là 0,4. Biết rằng xe chỉ không thể chạy được khi cả hai động cơ bị hỏng. Tính xác suất để xe đi được.

A.0,12    B.0,7    C.0,88    D.0,75

Lời giải:

Đáp án : C

+ Gọi A là biến cố “động cơ 1 bị hỏng” ⇒ P(A) = 0,3

+ Gọi B là biến cố “động cơ 2 bị hỏng” ⇒ P(B)= 0,4

Suy ra AB là biến cố “cả hai động cơ bị hỏng” hay “ xe không chạy được nữa”.

+ Do hai động cơ hoạt động độc lập nên A và B là hai biến cố độc lập.

+ Áp dụng quy tắc nhân xác suất ta được xác suất để xe không đi được nữa là

P(AB)= P(A).P(B)= 0,3.0,4= 0 ,12

Vậy xác suất để xe đi được là: 1- 0,12= 0,88

Câu 10: Một xạ thủ bắn bia. Biết rằng xác suất bắn trúng vòng tròn 10 là 0,2; vòng 9 là 0,25 và vòng 8 là 0,15. Nếu trúng vòng k thì được k điểm. Giả sử xạ thủ đó bắn ba phát súng một cách độc lập. Xả thủ đạt loại giỏi nếu anh ta đạt ít nhất 28 điểm. Xác suất để xả thủ này đạt loại giỏi

A.0,0935    B.0,0765    C.0,065    D.0,0875

Lời giải:

Đáp án : A

- Gọi H là biến cố: “Xạ thủ bắn đạt loại giỏi”.

A: “Ba viên trúng vòng ”

B: “Hai viên trúng vòng 10 và một viên trúng vòng 9”

C: “Một viên trúng vòng 10 và hai viên trúng vòng 9”

D: “Hai viên trúng vòng 10 và một viên trúng vòng 8”

Các biến cố A; B; C và D là các biến cố xung khắc từng đôi một và H=A∪B∪C∪D

Suy ra theo quy tắc cộng xác suất ta có:

P(H)= P(A)+ P(B) + P(C)+ P(D)

- Mặt khác:

P(A) = 0,2.0,2. 0,2= 0,008

P(B) = 0,2. 0,2. 0,25+ 0,2.0,25.0,2+ 0,25 . 0,2. 0,2= 0,03

P(C)= 0,2. 0,25. 0,25+ 0,25. 0,2. 0,25+ 0,25.0,25. 0.2 = 0,0375

P(D)= 0,2. 0,2. 0,15 + 0,2. 0,15. 0,2+ 0,15. 0,2. 0,2= 0,018

Do đó P(H) = 0,008+ 0,03+ 0,0375+0,018= 0,0935

Xem thêm các dạng bài tập Toán lớp 11 có trong đề thi THPT Quốc gia khác:

• Cách tìm xác suất của biến cố (cực hay có lời giải)
• Cách tính xác suất bài toán liên quan đến đếm số (cực hay có lời giải)
• Cách tính xác suất bài toán liên quan đến hình học (cực hay có lời giải)
• Cách giải bài tập Xác suất nâng cao, (cực hay có lời giải)
• Phương pháp giải bài tập Quy tắc cộng xác suất (cực hay có lời giải)
• Phương pháp giải bài tập Biến cố đối (cực hay có lời giải)

---