Bài tập lãi suất tổng hợp ôn thi Tốt nghiệp (có lời giải)
Bài tập lãi suất tổng hợp ôn thi Tốt nghiệp với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm các dạng bài tập về lãi suất.
Bài tập lãi suất tổng hợp ôn thi Tốt nghiệp (có lời giải)
(199k) Xem Khóa học Toán 12 KNTTXem Khóa học Toán 12 CDXem Khóa học Toán 12 CTST
Bài 1. Ông A mua chiếc xe ô tô trị giá 26 tỷ đồng tại Việt Nam. Sau mỗi tháng thì giá xe giảm 1% so với tháng trước đó. Hỏi sau 10 năm thì ông A bán chiếc xe đó đi thì được bao nhiêu ?
A.26. 109. 0,99120 ( đồng ). B. 26.109. 1,01120 ( đồng).
C. 26. 1,01120 ( tỉ đồng). D. 26. 0,99120 (tỉ đồng).
Lời giải:
Đáp án: A
Gọi T là giá xe còn lại sau tháng thứ n; a là giá ban đầu của chiếc xe, r là tỉ lệ bị giảm so với mỗi tháng.
Hết tháng thứ nhất: T1 = a − a. r = a( 1 − r)
Hết tháng thứ hai: T2 = T1 − T1.r = T1. (1 − r)= a. (1 − r)2
Hết tháng thứ ba: T3 = T2 − T2.r = T2. (1 − r) = a.(1 − r)3
………
Hết tháng thứ n : Tn = a. ( 1 − r)n .
Áp dụng công thức trên ta có: (10 năm =120 tháng)
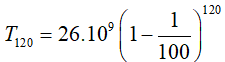
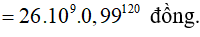
Bài 2. Lương khởi của một giáo viên là 3 triệu đồng/tháng. Cứ môi tháng đi dạy thì giáo viên đó sẽ được tăng thêm 3% so với mức lương khởi điểm. Hỏi sau 10 năm đi dạy liên tục thì mức lương sẽ là bao nhiêu ? (lương trả vào cuối tháng)
A. 3. (1,03)119 (triệu đồng). B. 3. (1, 03)120 (triệu đồng).
C. 3.106.(1,03)119 (triệu đồng). D. 3. 106.(1,03)120 (triệu đồng).
Lời giải:
Đáp án: A
Gọi a= 3 triệu đồng là mức lương khởi điểm của giáo viên , p= 3% là phần trăm mức lương mỗi tháng đi dạy tăng thêm, Hn số tiền cuối tháng thứ n giáo viên được nhận.
Cuối tháng thứ nhất: H1 = a
Cuối tháng thứ hai: H2 = H1.p +H1 = H1 .(1+ p)
Cuối tháng thứ ba: H3 = H2 .(1+ p) + H2.(1+ p).p = H2 ( 1+ p)2
……………..
Cuối tháng thứ n: Hn = a. (1+ p)n-1 n
Áp dụng công thức trên ta có:
Cuối năm thứ 10 , tức là cuối tháng thứ 10. 12= 120,mức lương khi đó là:

Bài 3. Ông A vay tiền của ngân hàng với số tiền là 500 triệu đồng. Để kết thúc hợp đồng ông và ngân hàng thỏa thuận chi trả như sau: Nếu trong vòng 3 năm đầu ông A hoàn vốn xong cho ngân hàng thì lãi suất được tính theo lãi đơn 12%/năm. Nếu qua thời gian đó cả vốn lẫn lãi thời gian đầu được định mức tính theo lãi kép (lãi của tháng trước được định làm vốn tiếp tục sinh lãi cho tháng sau) với lãi suất lúc này là 10%/năm. Sau đúng 6 năm hợp đồng ông A đã trả cho ngân hàng với số tiền là m triệu đồng, vậy giá trị gần đúng nhất của m là?
A. 900 triệu đồng. B. 910 triệu đồng. C. 905 triệu đồng. D. 915 triệu đồng.
Lời giải:
Đáp án: C
Đây là bài toán kết hợp cả lãi đơn và lãi kép.
* 3 năm đầu là lãi đơn. Số tiền cả gốc và lãi sau 3 năm đầu:
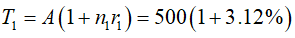
* 3 năm sau là lãi kép. Số tiền cả gốc và lãi sau 3 năm cuối:
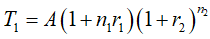
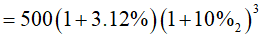
= 905,08 triệu đồng.
Bài 4. Bạn Hùng trúng tuyển vào Trường Đại học Ngoại Thương nhưng vì do không đủ tiền nộp học phí nên Hùng quyết định vay ngân hàng trong 4 năm môi năm 4 000 000 đồng để nộp học phí với lãi suất 3%/ năm. Sau khi tốt nghiệp Đại học, bạn Hùng phải trả góp hàng tháng cho ngân hàng số tiền t ( không đổi ) với lãi suất 0,25%/tháng trong vòng 5 năm. Tính số tiền t hàng tháng mà bạn Hùng phải trả cho ngân hàng (làm tròn đến kết quả hàng đơn vị )
A. 309 718,166 đồng B.312 518,166 đồng C. 398 402, 12 đồng D. 309 604,14 đồng
Lời giải:
Đáp án: A
+ Tiền vay từ năm thứ nhất đến khi tốt nghiệp (sau 4 năm), bạn Hùng nợ ngân hàng là
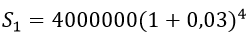 .
.
+ Tiền vay từ năm thứ hai đến khi tốt nghiệp (sau 3 năm), bạn Hùng nợ ngân hàng là
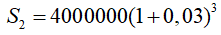
+ Tiền vay từ năm thứ ba đến khi tốt nghiệp (sau 2 năm), bạn Hùng nợ ngân hàng là
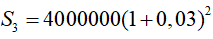
+ Tiền vay từ năm thứ 4 đến khi tốt nghiệp (sau 1 năm), bạn Hùng nợ ngân hàng là
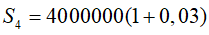 .
.
+ Tổng số tiền bạn Hùng nợ ngân hàng sau 4 năm là
S = S1 + S2 + S3 + S4
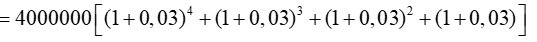
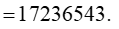
Lúc này ta xem như bạn Hùng nợ ngân hàng với số tiền ban đầu là S= 17236543
+ Cuối tháng thứ nhất bạn Hùng còn nợ: T1 = S.(1+ r) − A.
+ Cuối tháng thứ 2 bạn Hùng còn nợ:
T2 = T1.( 1+ r) − A = [S. (1+ r) − A].( 1+ r) − A = S.(1+ r)2 − A.[(1+r) + 1].
+ Cuối tháng thứ 3 bạn Hùng còn nợ:
T3 = T2. (1+ r) − A = S. (1+ r)3 − A[ (1+ r)2 + ( 1+ r)+ 1].
….
+ Cuối tháng thứ 60 bạn Hùng còn nợ:
T60 = S. (1+ r)60 − A[ (1+ r)59 +(1+ r)58 +...+( 1+ r) + 1]
Ta có T60 = 0
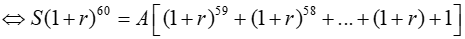
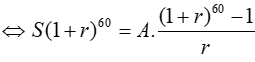
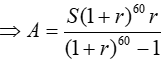
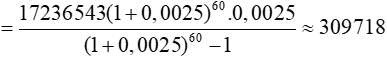
Bài 5. Theo dự báo với mức tiêu thụ dầu không đổi như hiện nay thì trữ lượng dầu của nước A sẽ hết sau 100 năm nữa. Nhưng do nhu cầu thực tế, mức tiêu thụ tăng lên 4% mỗi năm. Hỏi sau bao nhiêu năm số dầu dự trữ của nước A sẽ hết
A. 40 B. 41 C. 42 D.43
Lời giải:
Đáp án: B
Gọi x là lượng dầu tiêu thụ mỗi năm.
Lượng dầu dự trữ của nước A là 100x.
Tổng lượng dầu tiêu thụ thực tế trong n năm là
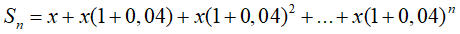
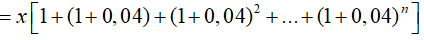
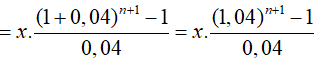
Ta có
Sn = 100x
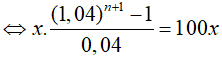
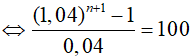
⇔ n ≈ 41
Bài 6. Ông An gửi gói tiết kiệm tích lũy cho con tại một ngân hàng với số tiền tiết kiệm ban đầu là 200.000.000 VNĐ, lãi suất 7%/ năm. Từ năm thứ hai trở đi, mỗi năm ông gửi thêm vào tài khoản với số tiền 20.000.000 VNĐ. Ông không rút lãi định kỳ hàng năm. Biết rằng, lãi suất định kỳ hàng năm không thay đổi. Hỏi sau 18 năm, số tiền ông An nhận được cả gốc lẫn lãi là bao nhiêu?
A. 1.335.967.000 VNĐ B. 1.686.898.000 VNĐ
C. 743.585.000 VNĐ D. 739.163.000 VNĐ
Lời giải:
Đáp án: A
Sau năm thứ nhất số tiền mà ông An nhận được là 200. (1+ 7%) ≈ 214 triệu đồng.
Đầu năm thứ hai, ông An gửi vào 20 triệu, nên đến cuối năm 2 số tiền ông nhận được là ( 214+ 20). (1+ 7%) triệu đồng.
Đầu năm thứ 3, ông An gửi vào 20 triệu đồng, nên đến cuối năm thứ 3, số tiền ông nhận được là:
[( 214+ 20).( 1+7%)+ 20].( 1+ 7%) = ( 214 + 20). (1+ 7%)2 +20.(1+ 7%)
Đầu năm thứ 4, ông An gửi vào 20 triệu đồng nên đến cuối năm thứ 4, số tiền ông nhận được là:
{[ 214+ 20). (1+ 7%)2 + 20.(1+ 7%)]+ 20}.( 1+ 7%)
=(214 + 20). ( 1+ 7%)+ 20 . (1+ 7%)2 + 20. (1+ 7%) triệu đồng.
…
Sau năm thứ 18, số tiền ông An nhận được là
A = (214+20).(1+7%)17 + 20.(1+7%).(1+(1+7%)+(1+7%)2+...+(1+7%)15 )
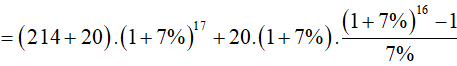
≈ 1335.967105 triệu đồng.
Bài 7. Bom nguyên tử là loại bom chứa Uranium-235 được phát nổ khi ghép các khối Uranium-235 thành một khối chứa 50kg tinh khiết. Uranium-235 có chu kỳ bán rã là 704 triệu năm. Nếu quả bom ban đầu chứa 64kg Uranium-235 tinh khiết và sau t triệu năm thì quả bom không thể phát nổ. Khi đó t thỏa mãn phương trình:
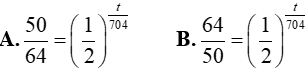
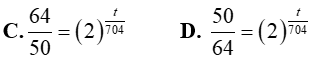
Lời giải:
Đáp án: A
Ở đây, sau t triệu năm quả bom không thể phát nổ, tức là trong khoảng thời gian t triệu năm đó thì quả bom không nổ, quả bom nổ và năm thứ t triệu tính từ thời điểm ban đầu.
Do chu kì bán rã của Uranium-235 là 704 triệu năm nên ta có
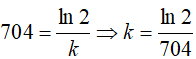
Sau t triệu năm quả bom không thể phát nổ nên
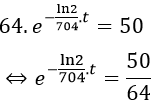
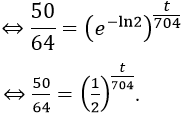
Bài 8. Cường độ một trận động đất được cho bởi công thức M = logA − logA0, với A là biên độ rung chấn tối đa và A0 là một biên độ chuẩn (hằng số). Đầu thế kỷ 20, một trận động đất ở San Francisco có cường độ đo được 8 độ Richter. Trong cùng năm đó, trận động đất khác ở Nhật Bản có cường độ đo được 6 độ Richer. Hỏi trận động đất ở San Francisco có biên độ gấp bao nhiêu lần biên độ trận động đất ở Nhật Bản?
A. 1000 lần B. 10 lần C. 2 lần D. 100 lần
Lời giải:
Đáp án: D
Nhận thấy ở San Francisco trận động đất có cường độ là:
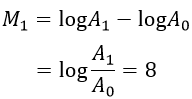
Ở Nhật Bản, trận động đất có cường độ là:
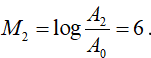
Khi đó .
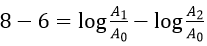
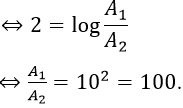
Bài 9. Cường độ của ánh sáng đi qua một môi trường không khí, chẳng hạn như nước, sương mù,… sẽ giảm dần tùy theo mức độ dày của môi trường và một hằng số μ gọi là khả năng hấp thu tùy thuộc môi trường theo công thức như sau: I = I0.e−μx với x là độ dày của môi trường đó, với x tính bằng mét. Biết rằng môi trường nước biển có μ = 14 . Hãy tính xem cường độ ánh sáng giảm đi bao nhiêu lần từ độ sâu 2 m xuống đến độ sâu 20 m?
A. e−25,2 B. e25,2 C. e12,6 D. e−12,6
Lời giải:
Đáp án: B
- Ở độ sâu 2m thì cường độ ánh sáng là
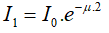
- Ở độ sâu 20m thì cường độ ánh sáng là
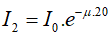
Khi đó ta có tỉ số
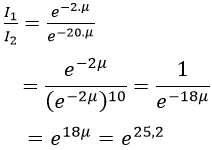
(199k) Xem Khóa học Toán 12 KNTTXem Khóa học Toán 12 CDXem Khóa học Toán 12 CTST
Xem thêm các dạng bài tập Toán lớp 12 ôn thi Tốt nghiệp có lời giải hay khác:
- Bài toán lãi đơn có lời giải
- Bài toán lãi kép có lời giải
- Bài toán Tiền gửi ngân hàng có lời giải
- Bài toán Gửi ngân hàng và rút tiền gửi hàng tháng có lời giải
- Bài toán Vay vốn trả góp có lời giải
- Bài toán Lãi kép liên tục có lời giải
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 12 Global Success
- Giải sgk Tiếng Anh 12 Smart World
- Giải sgk Tiếng Anh 12 Friends Global
- Lớp 12 Kết nối tri thức
- Soạn văn 12 (hay nhất) - KNTT
- Soạn văn 12 (ngắn nhất) - KNTT
- Giải sgk Toán 12 - KNTT
- Giải sgk Vật Lí 12 - KNTT
- Giải sgk Hóa học 12 - KNTT
- Giải sgk Sinh học 12 - KNTT
- Giải sgk Lịch Sử 12 - KNTT
- Giải sgk Địa Lí 12 - KNTT
- Giải sgk Giáo dục KTPL 12 - KNTT
- Giải sgk Tin học 12 - KNTT
- Giải sgk Công nghệ 12 - KNTT
- Giải sgk Hoạt động trải nghiệm 12 - KNTT
- Giải sgk Giáo dục quốc phòng 12 - KNTT
- Giải sgk Âm nhạc 12 - KNTT
- Giải sgk Mĩ thuật 12 - KNTT
- Lớp 12 Chân trời sáng tạo
- Soạn văn 12 (hay nhất) - CTST
- Soạn văn 12 (ngắn nhất) - CTST
- Giải sgk Toán 12 - CTST
- Giải sgk Vật Lí 12 - CTST
- Giải sgk Hóa học 12 - CTST
- Giải sgk Sinh học 12 - CTST
- Giải sgk Lịch Sử 12 - CTST
- Giải sgk Địa Lí 12 - CTST
- Giải sgk Giáo dục KTPL 12 - CTST
- Giải sgk Tin học 12 - CTST
- Giải sgk Hoạt động trải nghiệm 12 - CTST
- Giải sgk Âm nhạc 12 - CTST
- Lớp 12 Cánh diều
- Soạn văn 12 Cánh diều (hay nhất)
- Soạn văn 12 Cánh diều (ngắn nhất)
- Giải sgk Toán 12 Cánh diều
- Giải sgk Vật Lí 12 - Cánh diều
- Giải sgk Hóa học 12 - Cánh diều
- Giải sgk Sinh học 12 - Cánh diều
- Giải sgk Lịch Sử 12 - Cánh diều
- Giải sgk Địa Lí 12 - Cánh diều
- Giải sgk Giáo dục KTPL 12 - Cánh diều
- Giải sgk Tin học 12 - Cánh diều
- Giải sgk Công nghệ 12 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 12 - Cánh diều
- Giải sgk Giáo dục quốc phòng 12 - Cánh diều
- Giải sgk Âm nhạc 12 - Cánh diều




 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

