Các dạng bài toán thực tế ôn thi THPT Quốc gia chọn lọc, có đáp án

---

---

Các dạng bài toán thực tế ôn thi THPT Quốc gia chọn lọc, có đáp án

Phần Các dạng bài toán thực tế ôn thi đại học trong kì thi THPT Quốc gia sẽ tổng hợp Lý thuyết, các dạng bài tập chọn lọc có trong Đề thi THPT Quốc gia và trên 100 bài tập trắc nghiệm chọn lọc, có đáp án. Vào Xem chi tiết để theo dõi Các dạng bài toán thực tế tương ứng.

• Bài toán thực tế về hàm số mũ, logarit, lũy thừa Xem chi tiết
• 7 Bài toán lãi suất, bài toán thực tế trong đề thi Đại học có lời giải Xem chi tiết
• Dạng bài toán lãi đơn có lời giải Xem chi tiết
• Dạng bài toán lãi kép có lời giải Xem chi tiết
• Dạng bài toán Tiền gửi ngân hàng có lời giải Xem chi tiết
• Dạng bài toán Gửi ngân hàng và rút tiền gửi hàng tháng có lời giải Xem chi tiết
• Dạng bài toán Vay vốn trả góp có lời giải Xem chi tiết
• Dạng bài toán Lãi kép liên tục có lời giải Xem chi tiết
• Các dạng bài toán lãi suất hay có lời giải Xem chi tiết

Dạng bài toán lãi đơn ôn thi THPT Quốc gia

1. Phương pháp giải

- Định nghĩa: số tiền lãi chỉ tính trên số tiền gốc mà không tính trên số tiền lãi do số tiền gốc sinh ra, tức là tiền lãi của kì hạn trước không được tính vào vốn để tính lãi cho kì hạn kế tiếp, cho dù đến kì hạn người gửi không đến gửi tiền ra.

- Công thức tính: Khách hàng gửi vào ngân hàng A đồng với lãi đơn r% /kì hạn thì số tiền khách hàng nhận được cả vốn lẫn lãi sau n kì hạn (n ∈ N*) là:

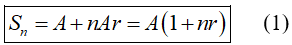
Chú ý: Trong tính toán các bài toán lãi suất và các bài toán liên quan, ta nhớ r% là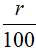

2. Ví dụ minh họa

Ví dụ 1. Chú Nam gửi vào ngân hàng 10 triệu đồng với lãi đơn 5%/năm thì sau 5 năm số tiền chú Nam nhận được cả vốn lẫn lãi là bao nhiêu?

A. 12,5 triệu B. 12 triệu C. 13 triệu D. 12, 8 triệu.

Hướng dẫn:

Đáp án: A

Số tiền cả gốc lẫn lãi chú Nam nhận được sau 5 năm là:

S₅ = 10.(1 + 5.0,05)= 12,5 (triệu đồng)

Ví dụ 2. Chị Hằng gửi ngân hàng 3 350 000 đồng, theo phương thức lãi đơn, với lãi suất 0,4 % trên nửa năm. Hỏi ít nhất bao lâu chị rút được cả vốn lẫn lãi là 4 020 000 đồng?

A. 5 năm. B. 30 tháng. C. 3 năm. D. 24 tháng.

Hướng dẫn:

Đáp án: B

Gọi n là số chu kỳ gửi ngân hàng, áp dụng công thức lãi đơn ta có:

4 020 000 = 3 350 000 ( 1 + n.0,04)

Suy ra, n= 5 (chu kỳ) .

Vậy thời gian là 5 . 6 = 30 tháng.

Ví dụ 3. Tính theo phương thức lãi đơn; để sau 2,5 năm rút được cả vốn lẫn lãi số tiền là 10 892 000 đồng với lãi suất 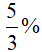một quý thì bạn phải gửi tiết kiệm số tiền bao nhiêu?

A. 9 336 000 B. 10 456 000. C.8 627 000. D. 9 215 000

Hướng dẫn:

Đáp án: A

Đây là bài toán lãi đơn với chu kỳ là một quý = 3 tháng.

Vậy 2,5 năm = 30 tháng = 10 quý ( 10 chu kỳ).

Với x là số tiền gửi tiết kiệm, ta có:

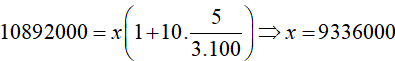
Dạng bài toán lãi kép ôn thi THPT Quốc gia

1. Phương pháp giải

- Định nghĩa

Lãi kép là nếu đến kì hạn người gửi không rút lãi ra thì tiền lãi được tính vào vốn của kì kế tiếp.

- Công thức tính

Khách hàng gửi vào ngân hàng A đồng với lãi kép r% /kì hạn thì số tiền khách hàng nhận được cả vốn lẫn lãi sau n kì hạn (n ∈ N*) là:

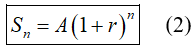
Chú ý: Từ công thức (2) ta có thể tính được:

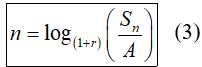
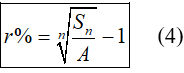
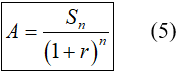
2. Ví dụ minh họa

Ví dụ 1. Chú Việt gửi vào ngân hàng 10 triệu đồng với lãi kép 5%/năm. Tính số tiền cả gốc lẫn lãi chú Việt nhận được sau khi gửi ngân hàng 10 năm (gần với số nào nhất)?

A. 16,234 triệu B. 16, 289 triệu C. 16, 327 triệu D.16, 280 triệu

Hướng dẫn:

Đáp án: B

Số tiền cả gốc lẫn lãi nhận được sau 10 năm với lãi kép 5%/năm là

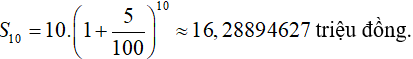
Ví dụ 2. Chú Việt gửi vào ngân hàng 10 triệu đồng .Với số tiền đó, nếu chú Việt gửi ngân hàng với lãi kép 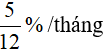thì sau 10 năm chú Việt nhận được bao nhiêu tiền?

A. 13,345 triệu B. 15,54 triệu C. 16,47 triệu D. 14,45 triệu

Hướng dẫn:

Đáp án: C

10 năm = 12.10= 120 tháng.

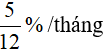
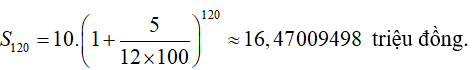
Số tiền cả gốc lẫn lãi nhận được sau 10 năm với lãi kép là

Ví dụ 3. Bạn An gửi tiết kiệm một số tiền ban đầu là 1000000 đồng với lãi suất 0,58%/tháng (không kỳ hạn). Hỏi bạn An phải gửi bao nhiêu tháng thì được cả vốn lẫn lãi bằng hoặc vượt quá 1300000 đồng ?

A. 46 tháng B. 44 tháng C. 45 tháng D. 47 tháng

Hướng dẫn:

Đáp án: A

Áp dụng công thức ( 3) ta có số kì hạn là:

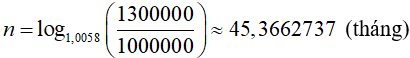
Nên để nhận được số tiền cả vốn lẫn lãi bằng hoặc vượt quá 1300000 đồng thì bạn An phải gửi ít nhất là 46 tháng.

Dạng bài toán Tiền gửi ngân hàng ôn thi THPT Quốc gia

1. Phương pháp giải

Định nghĩa

Mỗi tháng gửi đúng cùng một số tiền vào 1 thời gian cố định.

Công thức tính

Đầu mỗi tháng khách hàng gửi vào ngân hàng số tiền A đồng, với lãi kép r%/tháng thì số tiền khách hàng nhận được cả vốn lẫn lãi sau n tháng (n ∈ N*) ( nhận tiền cuối tháng, khi ngân hàng đã tính lãi) là S_n.

Ý tưởng hình thành công thức:

+ Cuối tháng thứ nhất, khi ngân hàng đã tính lãi thì số tiền có được là

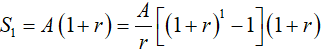
+ Đầu tháng thứ hai, khi đã gửi thêm số tiền đồng thì số tiền là

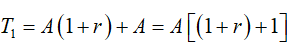
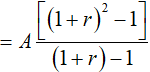
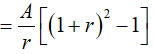
+ Cuối tháng thứ hai, khi ngân hàng đã tính lãi thì số tiền có được là

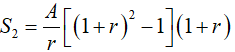
+ Từ đó ta có công thức tổng quát

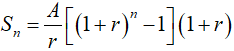
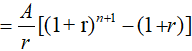
(6)

Chú ý: Từ công thức (6) ta có thể tính được:

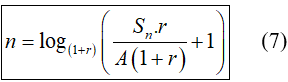
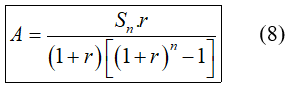
2. Ví dụ minh họa

Ví dụ 1. Đầu mỗi tháng ông Mạnh gửi ngân hàng 580 000 đồng với lãi suất 0,7%/tháng. Sau 10 tháng thì số tiền ông Mạnh nhận được cả gốc lẫn lãi (sau khi ngân hàng đã tính lãi tháng cuối cùng) là bao nhiêu?

A. 6 028 056 đồng B. 6 002 765 đồng

C. 6 012 654 đồng D. 6 001 982 đồng

Hướng dẫn:

Đáp án: A

Áp dụng công thức (6), số tiền ông Mạnh nhận được cả gốc lẫn lãi là:

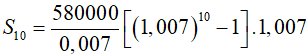
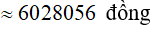
Ví dụ 2. Ông Nghĩa muốn có ít nhất 100 triệu đồng sau 10 tháng kể từ khi gửi ngân hàng với lãi 0,7%/tháng thì mỗi tháng ông Nghĩa phải gửi số tiền ít nhất bao nhiêu?

A. 9,623 triệu B. 9,622 triệu C. 9,723 triệu D. 9,564 triệu

Hướng dẫn:

Đáp án: B

Áp dụng công thức ( 8), số tiền mà ông Nghĩa cần gửi mỗi tháng là:

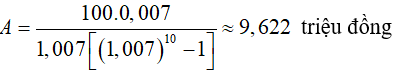
Ví dụ 3. Đầu mỗi tháng anh Thắng gửi vào ngân hàng số tiền 3 triệu đồng với lãi suất 0,6%/tháng. Hỏi sau ít nhất bao nhiêu tháng ( khi ngân hàng đã tính lãi) thì anh Thắng được số tiền cả gốc lẫn lãi từ 100 triệu trở lên?

A. 28 tháng B. 29 tháng C. 30 tháng D . 31 tháng.

Hướng dẫn:

Đáp án: C

Áp dụng công thức (7), số tháng ít nhất anh Thắng phải gửi để được số tiền cả gốc lẫn lãi từ 100 triệu trở lên là:

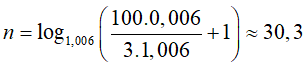
Vậy anh Thắng phải gửi ít nhất là 31 tháng mới được số tiền cả gốc lẫn lãi từ 100 triệu trở lên.

Xem thêm các chuyên đề Toán lớp 12 có trong đề thi THPT Quốc gia khác:

• Dạng bài tập Bất phương trình mũ trong đề thi Đại học có lời giải
• 5 dạng bài tập Bất phương trình logarit trong đề thi Đại học có lời giải
• 7 Bài toán lãi suất, bài toán thực tế trong đề thi Đại học có lời giải
• Tìm điều kiện xác định của lũy thừa hay nhất
• Dạng bài tập Rút gọn biểu thức chứa lũy thừa (cực hay)
• Dạng bài tập về so sánh các lũy thừa (cực hay)
• Dạng bài tập Tính giá trị của biểu thức lũy thừa (cực hay)
• Tìm điều kiện để biểu thức logarit xác định hay nhất

---

---

---