Bài toán thực tế lớp 12 Vectơ và tọa độ của vectơ trong không gian
Bài toán thực tế lớp 12 Vectơ và tọa độ của vectơ trong không gian có lời giải chương trình mới dùng chung cho ba sách Kết nối tri thức, Chân trời sáng tạo, Cánh diều với bài tập đa dạng giúp Giáo viên có thêm tài liệu giảng dạy các dạng toán thực tế lớp 12.
Bài toán thực tế lớp 12 Vectơ và tọa độ của vectơ trong không gian
Chỉ từ 300k mua trọn bộ Chuyên đề, các dạng Toán thực tế lớp 12 chương trình mới bản word trình bày đẹp mắt, chỉnh sửa dễ dàng:
- B1: gửi phí vào tk:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận đề thi
A. LÝ THUYẾT CẦN NHỚ
1. Vectơ trong không gian
Định nghĩa: Vectơ trong không gian là một đoạn thẳng có hướng.Độ dài của vectơ trong không gian là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó.
Chú ý: Tương tự như vectơ trong mặt phẳng, đối với vectơ trong không gian ta cũng có các kí hiệu và khái
niệm sau:
• Vectơ có điểm đầu là A và điểm cuối là B được kí hiệu là .
• Khi không cần chỉ rõ điểm đầu và điểm cuối của vectơ thì vectơ còn được kí hiệu là
• Độ dài của vectơ được kí hiệu là ||, độ dài của vectơ được kí hiệu là ||
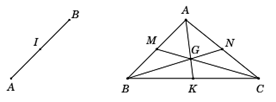
• Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ đó (Hình 1).
Hình 1. Đường thẳng d là giá của vectơ
Tương tự như trường hợp của vectơ trong mặt phẳng, ta có các khái niệm sau đối với vectơ trong không gian:
• Hai vectơ được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau.
• Nếu hai vectơ cùng phương thì chúng cùng hướng hoặc ngược hướng.
• Hai vectơ và được gọi là bằng nhau, kí hiệu = , nếu chúng có cùng độ dài và cùng hướng.
Chú ý: Tương tự như vectơ trong mặt phẳng, ta có tính chất và các quy ước sau đối với vectơ trong không gian:
• Trong không gian, với mỗi điểm O và vectơ cho trước, có duy nhất điểm M sao cho
• Các vectơ có điểm đầu và điểm cuối trùng nhau, ví dụ như gọi là các vectơ-không.
• Ta quy ước vectơ không có độ dài là 0, cùng hướng (và vì vậy cùng phương) với mọi vectơ.
• Do đó, các vectơ không đều bằng nhau và được kí hiệu chung là .
2. Tổng và hiệu của hai vectơ trong không gian
a) Tổng của hai vectơ trong không gian
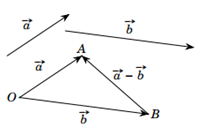
Trong không gian, cho hai vectơ và . Lấy một điểm O bất kì và các điểm A, B sao cho và . Khi đó, vectơ được gọi là tổng của hai vectơ và , ký hiệu là + .
Trong không gian, phép lấy tổng của hai vectơ được gọi là phép cộng vectơ.
Nhận xét: Quy tắc ba điểm và quy tắc hình bình hành trong mặt phẳng vẫn đúng trong không gian:
• Quy tắc ba điểm: Nếu A, B, C là ba điểm bất kì thì
• Quy tắc hình bình hành: Nếu ABCD là hình bình hành thì
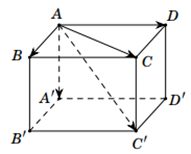
• Quy tắc hình hộp chữ nhật: Cho hình hộp . Ta có .
Hệ thức tương tự:
Chú ý: Tương tự như phép cộng vectơ trong mặt phẳng, phép cộng vectơ trong không gian có các tính chất sau:
• Tính chất giao hoán: Nếu và là hai vectơ bất kì thì .
• Tính chất kết hợp: Nếu , và là ba vectơ bất ki thì .
• Tính chất cộng với vectơ : Nếu là một vectơ bất kì thì .
Từ tính chất kết hợp của phép cộng vectơ trong không gian, ta có thể viết tổng của ba vectơ , và là mà không cần sử dụng các dấu ngoặc. Tương tự đối với tổng của nhiều vectơ trong không gian.
b) Hiệu của hai vectơ trong không gian
Vectơ đối: Trong không gian, vectơ có cùng độ dài và ngược hướng với vectơ được gọi là vectơ đối của vectơ
• Vectơ đối của kí hiệu là -
• Vectơ đối của là , nghĩa là (dùng để làm mất dấu trừ trước vectơ)
• Vectơ được coi là vectơ đối của chính nó
Định nghĩa: Trong không gian, cho hai vectơ , . Ta gọi là hiệu của hai vectơ và và kí hiệu là - . Phép lấy hiệu của hai vectơ được gọi là phép trừ vectơ.
Nhận xét:
• Với ba điểm O, A, B bất kì trong không gian thì ta có .
• Hai vectơ và đối nhau thì
3. Tích của một số với một vectơ trong không gian
Trong không gian, tích của một số thực k ≠ 0 với một vectơ là một vectơ, kí hiệu là k, được xác định như sau:
• Cùng hướng với vectơ nếu k > 0; ngược hướng với vectơ nếu k < 0
• Có độ dài bằng |k|.||.
Phép lấy tích của một số với một vectơ được gọi là phép nhân một số với một vectơ.
Chú ý: Quy ước nếu k = 0 hoặc .
• Nếu thì k = 0 hoặc .
• Trong không gian, điều kiện cần và đủ để hai vectơ và cùng phương là có một số thực k sao cho .
Hệ thức trung điểm, trọng tâm:
▪ Nếu I là trung điểm của đoạn thẳng AB thì ; ; ;…
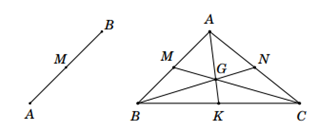
▪ Nếu G là trọng tâm của tam giác ABC thì ; ; ;…
Nhận xét:
▪ Với hai vectơ và bất kỳ, với mọi số h và k, ta luôn có:
•
•
•
•
•
•
▪ Hai vectơ và ( khác ) cùng phương khi và chỉ khi có số k sao cho
▪ Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi có số sao cho .
4. Tích vô hướng của hai vectơ trong không gian
Góc giữa hai vectơ
Trong không gian, cho hai vectơ khác . Lấy một điểm A bất kì và gọi B, Clà hai điểm sao cho . Khi đó, góc được gọi là góc giữa hai vectơ và , kí hiệu là ().
▪ Nếu cùng hướng với thì ; ngược hướng thì ; vuông góc thì
Định nghĩa tích vô hướng của hai vectơ: Trong không gian, cho hai vectơ khác . Tích vô hướng của hai vectơ và là một số, kí hiệu là , được xác định bởi công thức: .
▪ Trong trường hợp = 0 hoặc = 0 ta quy ước
▪
▪ Với hai vectơ khác , ta có
▪ Với hai vectơ khác , ta có
Tính chất: Với ba vectơ và số thực k ta có:
•
•
•
5. Hệ trục toạ độ trong không gian
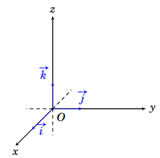
Định nghĩa: Trong không gian, ba trục đôi một vuông góc với nhau tại gốc O của mỗi trục.
Gọi lần lượt là các vectơ đơn vị trên các trục .
• Hệ ba trục như vậy được gọi là hệ trục toạ độ Descartes vuông góc hay đơn giản là hệ tọa độ .
• Điểm O được gọi là gốc toạ độ.
• Các mặt phẳng đôi một vuông góc với nhau được gọi là các mặt phẳng toạ độ.
• và
Không gian với hệ toạ độ còn được gọi là không gian .
6. Toạ độ của điểm
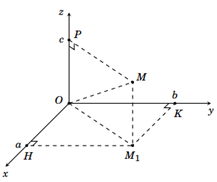
Trong không gian với hệ toạ độ , cho điểm M. Toạ độ điểm M được xác định như sau:
• Xác định hình chiếu M1 của điểm M trên mặt phẳng . Trong mặt phẳng toạ độ tìm hoành độ a, tung độ b của điểm M1.
• Xác định hình chiếu P của điểm M trên trục cao Oz, điểm P ứng với số c trên trục Oz. Số c là cao độ của điểm M.
• Bộ số là toạ độ điểm M trong không gian với hệ toạ độ , kí hiệu là
7. Toạ độ của vectơ
Trong không gian với hệ toạ độ
• Toạ độ điểm M cũng là toạ độ của vectơ
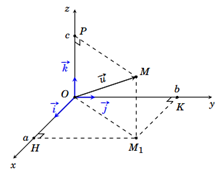
• Cho . Dựng điểm thoả mãn thì toạ độ của điểm M là toạ độ của .
Theo hình vẽ thì
Suy ra
• Toạ độ các vectơ đơn vị lần lượt là:
.
8. Biểu thức toạ độ của phép toán cộng, trừ, nhân một số thực với một vectơ
Trong không gian , cho hai vectơ và . Khi đó ta có:
•
•
• với k là một số thực.
Nhận xét: Vectơ cùng phương với vectơ khi và chỉ khi tồn tại số thực k sao cho
9. Biểu thức toạ độ tích vô hướng của hai vectơ
Trong không gian , tích vô hướng của hai vectơ và được xác định bởi công thức:
Nhận xét:
• Hai vectơ và vuông góc với nhau khi và chỉ khi .
• Nếu thì .
• Nếu và là hai vectơ khác thì
Chú ý: Nếu và thì .
Đặc biệt khi B trùng O ta nhận được công thức .
10. Biểu thức toạ độ tích có hướng của hai vectơ
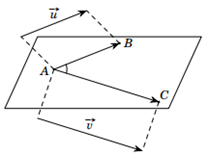
Trong không gian , cho hai vectơ và không cùng phương. Khi đó vectơ
vuông góc với hai vectơ và
▪ Vectơ xác định như trên gọi là tích có hướng của hai vectơ và kí hiệu là
▪ Quy ước 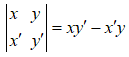
▪ không cùng phương với khi và chỉ khi
11. Biểu thức toạ độ trung điểm của đoạn thẳng, trọng tâm tam giác
Trong không gian , toạ độ trung điểm và trọng tâm được xác định như sau:
▪ Toạ độ trung điểm M của đoạn thẳng AB là .
▪ Toạ độ trọng tâm G của tam giác ABC là .
B. BÀI TẬP
Bài 1. Tính khoảng cách từ trọng tâm của một khối Rubik (đồng chất) hình tứ diện đều đến một mặt của nó, biết rằng chiều cao của khối Rubik là 8 cm.
Lời giải
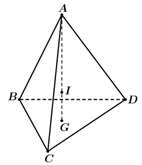
Giả sử khối Rubik (đồng chất) hình tứ diện đều được mô phỏng như hình vẽ.
Vì G là trọng tâm DBCD nên I là trọng tâm của tứ diện.
Vì ABCD là hình tứ diện đều nên và AG = 8 cm.
Mặt khác nên 3 điểm thẳng hàng và .
Do đó .
Bài 2. Ba sợi dây không giãn với khối lượng không đáng kể được buộc chung một đầu và được kéo căng về ba hướng khác nhau. Nếu các lực kéo làm cho ba sợi dây ở trạng thái đứng yên thì khi đó ba sợi dây nằm trên cùng một mặt phẳng. Hãy giải thích vì sao?
Lời giải
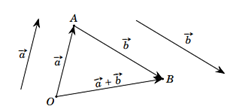
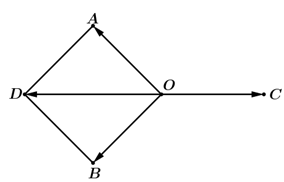
Giả sử lực kéo trên mỗi sợi dây được biểu diễn bởi các vectơ với là đầu chung của ba sợi dây. Khi ba sợi dậy cân bằng thì .
Vẽ hình bình hành OADB. Theo quy tắc hình bình hành thì .
Do đó .
Hay O là trung điểm của CD. Do đó các điểm cùng thuộc mặt phẳng (ABCD).
Suy ra ba sợi dây cùng nằm trong mặt phẳng đó.
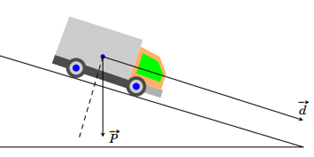
Bài 3. Cho biết A (đơn vị: J ) sinh bởi lực tác dụng lên một vật được tính bằng công thức trong đó là vectơ biểu thị độ dịch chuyển của vật (đơn vị: mét) khi chịu tác dụng của lực . Một chiếc xe có khối lượng 1,5 tấn đang đi xuống trên một đoạn đường dốc có góc nghiêm 5o so với phương ngang. Tính công sinh ra bởi trọng lực khi xe đi hết đoạn đường dốc dài 30 m (làm trong kết quả đến hàng đơn vị), biết rằng trọng lực được xác định bởi công thức , với m (đơn vị: kg) là khối lượng của vật và là gia tốc rơi tự do có độ lớn .
Bài 4. Một chất điểm A nằm trên mặt phẳng nằm ngang (), chịu tác động bởi ba lực . Các lực có giá nằm trong () và , còn lực có giá vuông góc với () và hướng lên trên. Xác định cường độ hợp lực của các lực biết rằng độ lớn của ba lực đó lần lượt là 20 N, 15 N và 10N.
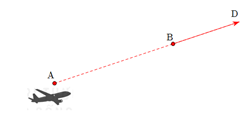
Bài 5. Trong không gian với một hệ trục toạ độ cho trước (đơn vị đo lấy theo km), ra đa phát hiện một chiếc máy bay di chuyển với vận tốc và hướng không đổi từ điểm đến điểm trong 10 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì toạ độ của máy bay sau 10 phút tiếp theo . Khi đó
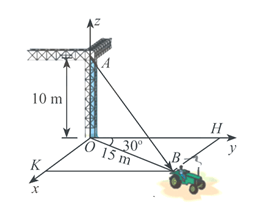
Bài 6. Một chiếc xe đang kéo căng sợi dây cáp AB trong công trường xây dựng, trên đó đã thiết lập hệ toạ độ như hình vẽ dưới với độ dài đơn vị trên các trục tọa độ bằng 1m. Tìm được tọa độ của vectơ . Khi đó tính a + c.
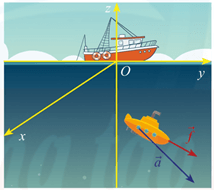
Bài 7. Một thiết bị thăm dò đáy biển như hình vẽ được đẩy bởi một lực (đơn vị: N) giúp thiết bị thực hiện độ dời (đơn vị: m). Tính công sinh bởi lực .
................................
................................
................................
Xem thêm Chuyên đề Toán thực tế lớp 12 chương trình mới có lời giải hay khác:
Bài toán thực tế lớp 12 Ứng dụng đạo hàm để giải quyết bài toán liên quan thực tiễn
Bài toán thực tế lớp 12 Ứng dụng nguyên hàm giải bài toán thực tiễn
Bài toán thực tế lớp 12 Ứng dụng tích phân giải bài toán thực tiễn liên quan đến Vật lí
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 12 Global Success
- Giải sgk Tiếng Anh 12 Smart World
- Giải sgk Tiếng Anh 12 Friends Global
- Lớp 12 Kết nối tri thức
- Soạn văn 12 (hay nhất) - KNTT
- Soạn văn 12 (ngắn nhất) - KNTT
- Giải sgk Toán 12 - KNTT
- Giải sgk Vật Lí 12 - KNTT
- Giải sgk Hóa học 12 - KNTT
- Giải sgk Sinh học 12 - KNTT
- Giải sgk Lịch Sử 12 - KNTT
- Giải sgk Địa Lí 12 - KNTT
- Giải sgk Giáo dục KTPL 12 - KNTT
- Giải sgk Tin học 12 - KNTT
- Giải sgk Công nghệ 12 - KNTT
- Giải sgk Hoạt động trải nghiệm 12 - KNTT
- Giải sgk Giáo dục quốc phòng 12 - KNTT
- Giải sgk Âm nhạc 12 - KNTT
- Giải sgk Mĩ thuật 12 - KNTT
- Lớp 12 Chân trời sáng tạo
- Soạn văn 12 (hay nhất) - CTST
- Soạn văn 12 (ngắn nhất) - CTST
- Giải sgk Toán 12 - CTST
- Giải sgk Vật Lí 12 - CTST
- Giải sgk Hóa học 12 - CTST
- Giải sgk Sinh học 12 - CTST
- Giải sgk Lịch Sử 12 - CTST
- Giải sgk Địa Lí 12 - CTST
- Giải sgk Giáo dục KTPL 12 - CTST
- Giải sgk Tin học 12 - CTST
- Giải sgk Hoạt động trải nghiệm 12 - CTST
- Giải sgk Âm nhạc 12 - CTST
- Lớp 12 Cánh diều
- Soạn văn 12 Cánh diều (hay nhất)
- Soạn văn 12 Cánh diều (ngắn nhất)
- Giải sgk Toán 12 Cánh diều
- Giải sgk Vật Lí 12 - Cánh diều
- Giải sgk Hóa học 12 - Cánh diều
- Giải sgk Sinh học 12 - Cánh diều
- Giải sgk Lịch Sử 12 - Cánh diều
- Giải sgk Địa Lí 12 - Cánh diều
- Giải sgk Giáo dục KTPL 12 - Cánh diều
- Giải sgk Tin học 12 - Cánh diều
- Giải sgk Công nghệ 12 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 12 - Cánh diều
- Giải sgk Giáo dục quốc phòng 12 - Cánh diều
- Giải sgk Âm nhạc 12 - Cánh diều


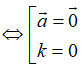
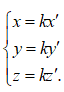
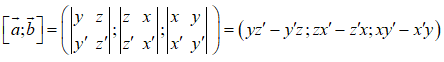




 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

