Bài toán thực tế về hàm số mũ, logarit, lũy thừa (cực hay)
Bài viết Bài toán thực tế về hàm số mũ, logarit, lũy thừa với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập Bài toán thực tế về hàm số mũ, logarit, lũy thừa.
Bài toán thực tế về hàm số mũ, logarit, lũy thừa (cực hay)
(199k) Xem Khóa học Toán 12 KNTTXem Khóa học Toán 12 CDXem Khóa học Toán 12 CTST
A. Phương pháp giải
1.Công thức lãi kép
a) Định nghĩa: Lãi kép là phần lãi của kì sau được tính trên số tiền gốc kì trước cộng với phần lãi của kì trước.
b) Công thức: Giả sử số tiền gốc là A; lãi suất r % /kì hạn gửi (có thể là tháng, quý hay năm).
● Số tiền nhận được cả gốc và lãi sau n kì hạn gửi là A( 1+ r) n
● Số tiền lãi nhận được sau n kì hạn gửi là A(1+r)n-A= A[(1+r)n-1]
2. Công thức lãi kép liên tục
Với só vốn ban đầu là A; theo thể thức lãi kép liên tục ; lãi suất mỗi năm là r thì sau N năm số tiền thu được cả vốn lẫn lãi là:
S= A.eN.r
B. Ví dụ minh họa
Câu 1:Bà Lan gửi 100 triệu vào tài khoản định kỳ tính lãi kép với lãi suất là 8%/năm. Tính số tiền lãi thu được sau 10 năm.
Lời giải:
Áp dụng công thức tính lãi kép, sau 10 năm số tiền cả gốc và lãi bà Hoa thu về là:
A(1+r) n= 100.(1+0,08)10 ≈215,892 triệu
Suy ra số tiền lãi bà Hoa thu về sau 10 năm là:
A(1+r)n-A=215,892-100=115,892 triệu.
Câu 2:Tỉ lệ tăng dân số hàng năm của Inđônêxialà 1,5%. Năm 1998, dân số của nước này là 212942000 người. Hỏi dần số của Inđônê xia vào năm 2006 gần với số nào sau đây nhất?
A.240091000
B.250091000
C.230091000
D.220091000
Lời giải:
Áp dụng công thức lãi kép liên tục An=A.eN.r
Với A= 212942000; r= 1,5%; n=2006-1998=8
Ta có A8= 212942000e1,5%.8≈240091434,6
Chọn A.
Câu 3:Một người gửi 15 triệu đồng vào ngân hàng theo thể thức lãi kép kỳ hạn một quý với lãi suất 1,65% một quý. Hỏi sau bao nhiêu quý thì người đó có được ít nhất 20 triệu ?
A.15 quý.
B.16 quý.
C.17 quý.
D.18 quý
Lời giải:
Áp dụng công thức lãi kép : An= A0 (1+r)n
Với A0 =15; An=20; r=1,65% . Ta đi tính n
Theo yêu cầu bài toán ta có:
Chọn D
Câu 4:Sau nhiều năm làm việc anh Ngọc tiết kiệm được P đồng, dự định số tiền đó để mua một căn nhà. Nhưng hiện nay với số tiền đó thì anh ta chưa thể mua được ngôi nhà vì giá trị ngôi nhà mà anh ta muốn mua là 2P đồng. Vì vậy anh Ngọc gửi tiết kiệm số tiền này vào ngân hàng Vietcombank. Theo bạn sau bao nhiêu năm anh Ngọc mới có thể sở hữu được ngôi nhà đó. Biết rằng lãi suất gởi tiết kiệm là 8,4% một năm , lãi hằng năm được nhập vào vốn và giá của ngôi nhà đó không thay đổi trong 12 năm tới. ( Kết quả làm tròn đến hàng đơn vị)
A.9 năm.
B.10 năm.
C.8 năm.
D.11 năm.
Lời giải:
Áp dụng công thức lãi kép; tính số tiền lĩnh sau n năm gởi tiết kiệm với lãi suất như trên là Pn= P0(1+0,084)n=P(1,084)n
Theo yêu cầu bài toán đặt ra, ta có:
Câu 5:Một người gửi tiết kiệm theo ngân hàng một số tiền là 500 triệu đồng, có kì hạn 3 tháng (sau 3 tháng mới được rút tiền), lại suất 5,2% một năm, lãi nhập gốc (sau 3 tháng người đó không rút tiền ra thì tiền lãi sẽ nhập vào gốc ban đầu). Để có số tiền ít nhất là 561 triệu động thì người đó phải gửi bao nhiêu tháng ? ( Kết quả làm tròn hàng đơn vị)
A.25 tháng.
B.27 tháng.
C.26 tháng.
D.28 tháng.
Lời giải:
Áp dụng công thức An= A0(1+r)n
Với A0= 500; An= 561; 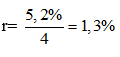
Theo yêu cầu bài toán ta có:
Do đó cần gửi 9 quý tức là 3.9=27 tháng.
Chọn B.
Câu 6:Một học sinh 16 tuổi được hưởng tài sản thừa kế 200 000 000 VNĐ. Số tiền này được bảo quản trong một ngân hàng với kì hạn thanh toán 1 năm và học sinh này chỉ nhận được số tiền này khi đã đủ 18 tuổi. Biết rằng khi đủ 18 tuổi, số tiền mà học sinh này được nhận sẽ là 228 980 000 VNĐ. Vậy lãi suất kì hạn 1 năm của ngân hàng này là bao nhiêu ?
A.6% / năm.
B.5% / năm.
C.7% / năm.
D.8% / năm.
Lời giải:
Áp dụng công thức lãi kép
Với A0=200 000 000; A2= 228 980 000; n=2 . Ta đi tính r
Khi đó:
Chọn C.
Câu 7:Lãi suất của tiền gửi tiết kiệm của một ngân hàng thời gian qua liên tục thay đổi. Bạn Hoàng gửi số tiền ban đầu là 5 triệu đồng với lãi suất 0,7% tháng. Chưa đầy một năm, thì lãi suất tăng lên 1,15% tháng trong nửa năm tiếp theo và bạn Hoàng tiếp tục gửi. Sau nửa năm đó lãi suất giảm xuống còn 0,9% tháng. Bạn Hoàng tiếp tục gửi thêm một số tháng tròn nữa. Biết rằng khi rút ra số tiền bạn Hoàng nhận được cả vốn lẫn lãi là 5747478,359 đồng (chưa làm tròn). Hỏi bạn Hòang đã gửi tiết kiệm trong bao nhiêu tháng ? (Trong suốt quá trình gửi thì lãi nhập gốc)
A . 15 tháng.
B. 16 tháng.
C. 14 tháng.
D. 19 tháng.
Lời giải:
Gọi n là số tháng gửi với lãi suất 0,7% tháng và m là số tháng gửi với lãi suất 0,9% tháng.
Khi đó, số tiền gửi cả vốn lẫn lãi là:
5 000 000 (1+ 0,07)n (1+0, 0115)6.(1+0,09)m= 5 747 478,359
Don là số tự nhiên và 1 ≤ n ≤ 12 nên ta thử lần lượt các giá trị là 2, 3, 4, 5,... đến khi tìm được m∈N
Sử dụng MTCT ta tìm được n=5 và m=4.
Do đó số tháng bạn Hoàng đã gửi là 15.
C. Bài tập vận dụng
Câu 1:Bố Tùng để dành cho Tùng 11000 USD để học đại học trong ngân hàng theo hình thức lãi kép với lãi suất 0,73% một tháng. Mỗi tháng Tùng đến rút 60USD để sinh sống.Hỏi sau một năm số tiền còn lại là bao nhiêu? ( Kết quả làm tròn đến hàng đơn vị)
A.11254USD.
B.1259USD.
C.1257USD.
D.1256USD.
Lời giải:
Nếu mỗi tháng Tùng không rút tiền thì sau n tháng Tùng có số tiền là: a(1+r)n
Nhưng do mỗi tháng Tùng rút 60 USD nên sau n tháng số tiền còn lại trong tài khoản là:
Với a=11 000 USD; x= 60USD; r=0,73%. Ta đi tính Pn+1
Số tiền trong ngân hàng sau 1 năm ( 12 tháng) là
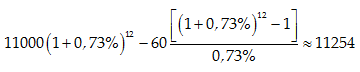
Số tiền còn lại sau 1 năm là : 11254USD
Chọn A.
Câu 2:Biết rằng tỉ lệ giảm dân hàng năm của Nga là 0,5%. Năm 1998, dân số của Nga là 146861000 người. Hỏi năm 2008 dân số của Nga gần với số nào sau đây nhất?
A.135 699 000
B.139 699 000
C.140 699 000
D.145 699 000
Lời giải:
Áp dụng công thức lãi kép liên tục
Với A0 =146 861 000; r= -0,5%; n=2008-1998= 10
Ta có A10= 146 861 000.e-0,5%.10= 139 527 283, 2
Chọn B.
Câu 3:Tỉ lệ tăng dân số hàng năm của Nhật là 0,2%. Năm 1998, dân số của Nhật là 125 932 000. Vào năm nào dân số của Nhật sẽ là 140 000 000 ? ( Kết quả làm tròn đến hàng đơn vị)
A.2061.
B.2055.
C.2051.
D.2045.
Lời giải:
Áp dụng công thức lãi kép liên tục
Với A0= 125 932 000; r= 0,2%; An= 140 000 000.Ta đi tính n.
Ta có
Đến năm 53+ 1998= 2051 thì dân số của Nhật xấp xỉ là 140 000 000
Chọn C.
Câu 4:Nếu cường độ âm tăng lên 1000 lần thì độ to của âm thay đổi như thế nào?
A.Tăng 10 dB.
B.Tăng 3 lần.
C.Giảm 30dB.
D.Tăng 30 dB.
Lời giải:
Ta có
Chọn D
Câu 5:Áp suất không khí P ( đo bằng milimet thuỷ ngân, kí hiệu là mmHg) suy giảm mũ so với độ cao x( đo bằng mét), tức P giảm theo công thức P = P0. exi trong đó P0= 760mmHg là áp suất ở mực nước biển ( x=0), i là hệ số suy giảm. Biết rằng ở độ cao 1000m thì áp suất của không khí là 672,71mmHg . Hỏi áp suất không khí ở độ cao 3000 m gần với số nào sau đây nhất?
A.530,23mm Hg.
B.540,23mmHg.
C.520,23mmHg.
D.510,23 mmHg
Lời giải:
Áp dụng công thức P= P0 exi
Ở độ cao 1000m ta có : P0= 760mm Hg ; n=1000m ; P=672,71mmHg
Từ giả thiết này ta tìm được hệ số suy giảm i. Ta có
Khi đó ở độ cao 3000 m, áp suất của không khí là :
Chọn A.
Câu 6:: Một khu rừng có trữ lượng gỗ 4. 105 mét khối. Biết tốc độ sinh trưởng của các cây ở khu rừng đó là 4% mỗi năm. Hỏi sau 5 năm, khu rừng đó sẽ có bao nhiêu mét khối gỗ ?
A.545470
B.488561
C.465470
D.535470
Lời giải:
Áp dụng công thức An= A0. en.r
Với A0= 4.105 ; r= 4% ; n=5
Sau 5 năm , khu rừng đó sẽ có số mét khối gỗ là :
A5= 4.105.e4%.5≈488561
Chọn B.
Câu 7:Trong vật lí, sự phân rã của các chất phóng xạ được biểu diễn bằng công thức : 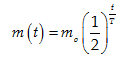
A.22,097 (gam).
B.23,097 (gam).
C.20,097 (gam).
D. 24,097 (gam
Lời giải:
Áp dụng công thức
Với m0= 250; T=24 giờ = 1 ngày; t=3,5 ngày đêm
Ta có 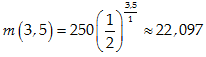
Chọn A.
Câu 8:Năm 1994, tỉ lệ thể tích khí CO2 trong không khí là 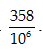
A.393.10-6.
B.379.10-6.
C.373.10-6.
D.354.10-6.
Lời giải:
Áp dụng công thức An= A0.en.r
Với
Ta có
Chọn C
Câu 9:Sự tăng trưởng của một loại vi khuẩn tuân theo công thức S= A.ert,trong đó A là số lượng vi khuẩn ban đầu, r là tỉ lệ tăng trưởng ( r > 0 ), t là thời gian tăng trưởng. Biết rằng số lượng vi khuẩn ban đầu là 100 con và sau 5 giờ có 300 con. Để số lượng vi khuẩn ban đầu sẽ tăng gấp đôi thì thời gian tăng trưởng t gần với kết quả nào sau đây nhất.
A.3 giờ 9 phút.
B.3 giờ 2 phút.
C.3 giờ 16 phút.
D.3 giờ 30 phút.
Lời giải:
Trước tiên, ta tìm tỉ lệ tăng trưởng mỗi giờ của loài vi khuẩn này. Từ giả thiết
Tức là tỉ lệ tăng trưởng của loại vi khuẩn này là 21,97 % mỗi giờ.
Từ 100 con, để có 200 con thì thời gian cần thiết là bao nhiêu? Từ công thức 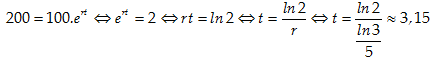
Chọn A.
Câu 10:: Cường độ một trận động đất M (richter) được cho bởi công thức M= log A-log A0, với A là biên độ rung chấn tối đa và A0 là một biên độ chuẩn (hằng số). Đầu thế kỷ 20, một trận động đất ở San Francisco có cường độ 8 độ Richter. Trong cùng năm đó, trận động đất khác Nam Mỹ có biên độ mạnh hơn gấp 4 lần. Cường độ của trận động đất ở Nam Mỹ gần với số nào sau đây nhất là:
A.7,9.
B.8,6.
C.8,5.
D.8,9.
Lời giải:
• Trận động đất ở San Francisco có cường độ 8 độ Richte khi đó áp dụng công thức
M1= log A- logA0 suy ra 8= log A-logA0
• Trận động đất ở Nam Mỹ có biên độ là 4A, khi đó cường độ của trận động đất ở Nam Mỹ là:
Chọn B.
Câu 11:: Một người gửi 100 triệu đồng vào ngân hàng với kì hạn 3 tháng (1 quí), lãi suất 6% một quí theo hình thức lãi kép ( lãi cộng với vốn). Sau đúng 6 tháng, người đó lại gửi thêm 100 triệu đồng với hình thức và lãi suất như trên. Hỏi sau 1 năm tính từ lần gửi đầu tiên người đó nhận số tiền gần với kết quả nào nhất?
A.239 triệu đồng.
B.230 triệu đồng.
C.243 triệu đồng.
D.236 triệu đồng.
Lời giải:
Áp dụng công thức An== A0(1+ r) n
Giai đoạn 1: Gửi 100 triệu : Áp dụng công thức trên với A0= 100; r= 6%=0,06; n=4 .
Số tiền thu được sau 1 năm – tức 4 quý là: A4= 100(1+0,06)4triệu đồng.
Giai đoạn 2: Sau đúng 6 tháng gửi thêm 100 triệu : Áp dụng công thức trên với
A0= 100; r= 6%= 0,06; n=2 .
Số tiền thu được thêm sau 2 quí cuối năm là: A2=100(1+0,06)2triệu đồng.
Vậy tổng số tiền người đó thu được sau một năm là: A= A4+ A2=238,6077 triệu đồng.
Chọn A.
Câu 12:Năng lượng giải toả E của một trận động đất tại tâm địa chấn ở M độ Richte được xác định bởi công thức: log( E)=11,4+ 1,5M . Vào năm 1995, Thành phố X xảy ra một trận động đất 8 độ Richte và năng lượng giải toả tại tâm địa chấn của nó gấp 14 lần trận động đất ra tại thành phố Y vào năm 1997. Hỏi khi đó độ lớn của trận động đất tại thành phố Y là bao nhiêu? ( kết quả làm tròn đến hàng phần trục)
A. 7,2 độ Richte
B. 7,8 độ Richte.
C. 8,3 độ Richte.
D. 6,8 độ Richte.
Lời giải:
Ta có năng lượng giải toả của trận động đất ở thành phố X tại tâm địa chấn là:
logE1= 11,4+ 1,5.M1 suy ra log E1 =11,4+1,5.8
do đó: E1=10 23,4
Khi đó theo giả thiết năng lượng giải toả của trận động đất ở thành phố Y tại tâm địa chấn là:
Gọi M2 độ lớn của trận động đất tại thành phố Y, áp dụng công thức
log (E) =11,4+1,5M ta được phương trình sau:
Chọn A.
Câu 13:Một người gửi ngân hàng 100 triệu đồng theo hình thức lãi đơn, kì hạn 3 tháng với lãi suất 3% một quý. Hỏi người đó phải gửi trong ngân hàng ít nhất bao lâu, số tiền thu về hơn gấp hai số tiền vốn ban đầu?
A.102 tháng.
B.103 tháng.
C.100 tháng.
D.101 tháng.
Lời giải:
Áp dụng công thức lãi đơn ta có: A n= A0(1+ nr) , số tiền thu về hơn gấp hai lần số vốn ban đầu ta có:
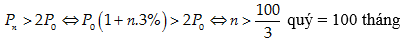
Suy ra để số tiền thu về hơn gấp hai số tiền vốn ban đầu cần gửi ít nhất 101 tháng.
Chọn D.
Câu 14:Một người gửi 15 triệu đồng vào ngân hàng theo thể thức lãi kép kỳ hạn 1 quý với lãi suất 1,65% một quý. Hỏi sau bao lâu người đó có được ít nhất 20 triệu đồng cả vốn lẫn lãi từ số vốn ban đầu?
A.sau khoảng 4 năm 6 tháng.
B.sau khoảng 4 năm 3 tháng .
C.sau khoảng 4 năm 2 tháng.
D.sau khoảng 4 năm 9 tháng.
Lời giải:
Áp dụng công thức lãi kép ta có số tiền cả vốn lẫn lãi người gửi sau n quý là
An= 15( 1+1,65%)n=15.1,0165n (triệu đồng)
Từ đó ta có :
Để có số tiền An= 20 triệu đồng thì phải sau một thời gian là:
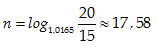
Vậy sau khoảng 4 năm 6 tháng ( 4 năm 2 quý), người gửi sẽ có ít nhất 20 triệu đồng từ số vốn ban đầu 15 triệu đồng ( vì hết quý thứ hai, người gửi mới được nhận lãi của quý đó.
Chọn A.
Câu 15:Một người gửi vào ngân hàng 100 triệu đồng với kì hạn 3 tháng, lãi suất 5% một quý theo hình thức lãi kép (sau 3 tháng sẽ tính lãi và cộng vào gốc). Sau đúng 6 tháng, người đó gửi thêm 50 triệu đồng với kì hạn và lãi suất như trước đó. Cho biết số tiền cả gốc và lãi được tính theo công thức T= A(1+r) n, trong đó A là số tiền gửi, r là lãi suất và n là số kì hạn gửi. Tính tổng số tiền người đó nhận được 1 năm sau khi gửi tiền.( Xấp xỉ 3 chữ số thập phân)
A. 176, 676 triệu đồng.
B.178,676 triệu đồng.
C. 177,676 triệu đồng.
D.179,676 triệu đồng.
Lời giải:
Bài toán chia làm 2 giai đoạn
Giai đoạn 1 (6 tháng đầu tiên) ta có:
A1= 100 (triệu đồng), n=2 (6 tháng = 2 kỳ, với mỗi kỳ 3 tháng)và r= 0,05.
Áp dụng công thức T1= A1( 1+ r)n= 100(1+ 0,05) 2=110,25 (triệu đồng).
Giai đoạn 2 (6 tháng cuối của 1 năm)
A2= T1= 110, 25+50 =160,25 (triệu đồng), n =2 (6 tháng = 2 kỳ, với mỗi kỳ 3 tháng) và r= 0,05.
Áp dụng công thức T2= A2( 1+ r) n= 160,25( 1+ 0,05)2= 176,676 (triệu đồng).
Chọn A.
Câu 16:Sự tăng trưởng của một loài vi khuẩn được tính theo công thứcf(t) =Aert, trong đó A là số lượng vi khuẩn ban đầu, r là tỷ lệ tăng trưởng ( r > 0) , t (tính theo giờ) là thời gian tăng trưởng. Biết số vi khuẩn ban đầu có 1000 con và sau 10 giờ là 5000 con. Hỏi sao bao lâu thì số lượng vi khuẩn tăng gấp 10 lần.
A. 5ln20 (giờ)
B. 5ln10 (giờ)
C. 10log510 (giờ)
D.10log520(giờ)
Lời giải:
Số vi khuẩn ban đầu có 1000 con và sau 10 giờ là 5000 con. Áp dụng công thức
f(t) = Aert, ta có:
Gọi là thời gian cần tìm để số lượng vi khuẩn tăng gấp 10 lần.
Do đó: 1000=1000ert suy ra ert= 10 nên rt= ln10
Chọn câu C.
Xem thêm các bài toán thực tế lớp 12 chọn lọc, hay khác:
- 7 Bài toán lãi suất, bài toán thực tế ôn thi Tốt nghiệp (có lời giải)
- Bài toán lãi đơn có lời giải
- Bài toán lãi kép có lời giải
- Bài toán Tiền gửi ngân hàng có lời giải
- Bài toán Gửi ngân hàng và rút tiền gửi hàng tháng có lời giải
- Bài toán Vay vốn trả góp có lời giải
- Bài toán Lãi kép liên tục có lời giải
- Bài tập lãi suất tổng hợp ôn thi Tốt nghiệp
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 12 Global Success
- Giải sgk Tiếng Anh 12 Smart World
- Giải sgk Tiếng Anh 12 Friends Global
- Lớp 12 Kết nối tri thức
- Soạn văn 12 (hay nhất) - KNTT
- Soạn văn 12 (ngắn nhất) - KNTT
- Giải sgk Toán 12 - KNTT
- Giải sgk Vật Lí 12 - KNTT
- Giải sgk Hóa học 12 - KNTT
- Giải sgk Sinh học 12 - KNTT
- Giải sgk Lịch Sử 12 - KNTT
- Giải sgk Địa Lí 12 - KNTT
- Giải sgk Giáo dục KTPL 12 - KNTT
- Giải sgk Tin học 12 - KNTT
- Giải sgk Công nghệ 12 - KNTT
- Giải sgk Hoạt động trải nghiệm 12 - KNTT
- Giải sgk Giáo dục quốc phòng 12 - KNTT
- Giải sgk Âm nhạc 12 - KNTT
- Giải sgk Mĩ thuật 12 - KNTT
- Lớp 12 Chân trời sáng tạo
- Soạn văn 12 (hay nhất) - CTST
- Soạn văn 12 (ngắn nhất) - CTST
- Giải sgk Toán 12 - CTST
- Giải sgk Vật Lí 12 - CTST
- Giải sgk Hóa học 12 - CTST
- Giải sgk Sinh học 12 - CTST
- Giải sgk Lịch Sử 12 - CTST
- Giải sgk Địa Lí 12 - CTST
- Giải sgk Giáo dục KTPL 12 - CTST
- Giải sgk Tin học 12 - CTST
- Giải sgk Hoạt động trải nghiệm 12 - CTST
- Giải sgk Âm nhạc 12 - CTST
- Lớp 12 Cánh diều
- Soạn văn 12 Cánh diều (hay nhất)
- Soạn văn 12 Cánh diều (ngắn nhất)
- Giải sgk Toán 12 Cánh diều
- Giải sgk Vật Lí 12 - Cánh diều
- Giải sgk Hóa học 12 - Cánh diều
- Giải sgk Sinh học 12 - Cánh diều
- Giải sgk Lịch Sử 12 - Cánh diều
- Giải sgk Địa Lí 12 - Cánh diều
- Giải sgk Giáo dục KTPL 12 - Cánh diều
- Giải sgk Tin học 12 - Cánh diều
- Giải sgk Công nghệ 12 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 12 - Cánh diều
- Giải sgk Giáo dục quốc phòng 12 - Cánh diều
- Giải sgk Âm nhạc 12 - Cánh diều

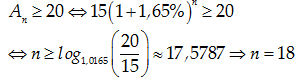
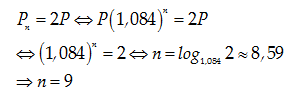
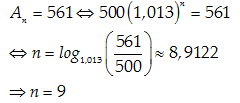
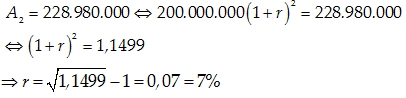
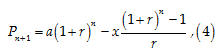
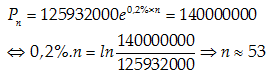
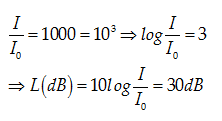
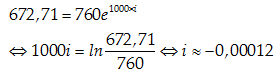
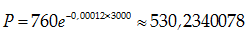
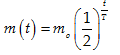
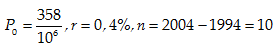
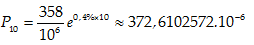
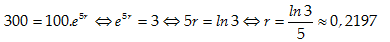
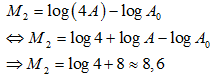
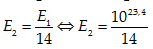
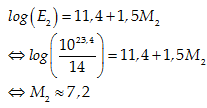
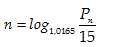
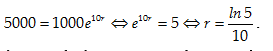
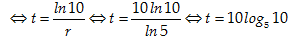



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

