Bài toán Lãi kép liên tục ôn thi Tốt nghiệp (có lời giải)
Bài toán thực tế Lãi kép liên tục ôn thi Tốt nghiệp với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài toán Lãi kép liên tục.
Bài toán Lãi kép liên tục ôn thi Tốt nghiệp (có lời giải)
(199k) Xem Khóa học Toán 12 KNTTXem Khóa học Toán 12 CDXem Khóa học Toán 12 CTST
1. Phương pháp giải
- Đinh nghĩa.
* Gửi vào ngân hàng A đồng với lãi kép r%/năm thì số tiền nhận được cả vốn lẫn lãi sau n năm (n ∈ N*) là: Sn = A. (1+ r)n
* Giả sử ta chia mỗi năm thành m kì hạn để tính lãi và lãi suất mỗi kì hạn là 

Khi tăng số kì hạn của mỗi năm lên vô cực, tức là m → +∞ , gọi là hình thức lãi kép tiên tục thì người ta chứng minh được số tiền nhận được cả gốc lẫn lãi là:
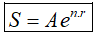
Công thức trên còn gọi là công thức tăng trưởng mũ.
2. Ví dụ minh họa
Ví dụ 1. Sự tăng trưởng dân số được ước tính theo công thức tăng trưởng mũ. Biết rằng tỉ lệ tăng dân số thế giới hàng năm là 1,32%, năm 2013 dân số thế giới vào khoảng 7095 triệu người. Khi đó dự đoán dân số thế giới năm 2020 sẽ là bao nhiêu?
A. 7782 triệu người B.7652 triệu người
C. 7821 triệu người D. 7689 triệu người
Lời giải:
Đáp án: A
Theo công thức tăng trưởng mũ thì dự đoán dân số năm 2010 là

Ví dụ 2. Biết rằng đầu năm 2010, dân số Việt Nam là 86932500 người và tỉ lệ tăng dân số năm đó là 1,7% và sự tăng dân số được tính theo công thức tăng trưởng mũ. Hỏi cứ tăng dân số với tỉ lệ như vậy thì đến năm nào dân số nước ta ở mức 100 triệu người?
A. 2016 B. 2017 C. 2018 D. 2019
Lời giải:
Đáp án: C
Theo công thức tăng trưởng mũ thì dự đoán dân số năm 2010 là
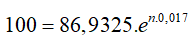

Ví dụ 3. Tỉ lệ tăng dân số hàng năm của In-đô-nê-xi-a là 1,5%. Năm 1998, dân số của nước này là 212 942 000 người. Hỏi dần số của In-đô-nê-xi-a vào năm 2006 gần với số nào sau đây nhất?
A. 240091000 B.250091000. C.230091000 D.220091000
Lời giải:
Đáp án: A
Áp dụng công thức tăng trưởng dân số Pn = P0.en.r
Với n = 2006 − 1998 = 8; r = 1,5 % và Po= 212942000
Ta có
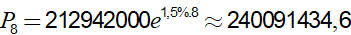
Ví dụ 4. Biết rằng tỉ lệ giảm dân hàng năm của Nga là 0, 5%. Năm 1998, dân số của Nga là 146861000 người. Hỏi năm 2008 dân số của Nga gần với số nào sau đây nhất?
A. 135699000. B.139699000. C.140699000. D.145699000
Lời giải:
Đáp án: B
Áp dụng công thức tăng trưởng dân số Pn = P0.en.r
Với n = 2008 − 1998 = 10; r = − 0,5 % và Po= 146861000
Ta có

Ví dụ 5. Áp suất không khí P ( đo bằng milimet thuỷ ngân, kí hiệu là mmHg) suy giảm mũ so với độ cao x (đo bằng mét), tức P giảm theo công thức P= P0.ex.i trong đó Po= 760 mmHg là áp suất ở mực nước biển ( x = 0 ), i là hệ số suy giảm. Biết rằng ở độ cao 1000 m thì áp suất của không khí là 672, 71 mmHg. Hỏi áp suất không khí ở độ cao 3000 m gần với số nào sau đây nhất?
A. 530, 23 mmHg. B. 540, 23 mmHg. C. 520,23 mmHg. D. 510, 23 mmHg.
Lời giải:
Đáp án: A
Áp dụng công thức P=P0. ex.i với P0 = 760; x = 1000 thì P = 672,71
Ta tìm được hệ số suy giảm


Vậy với x= 3000 thì
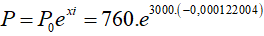
= 527,0558042
Gần với đáp án A nhất.
Ví dụ 6. Sự tăng trưởng của một loại vi khuẩn tuân theo công thức S= A. ert ,trong đó A là số lượng vi khuẩn ban đầu, r là tỉ lệ tăng trưởng ( r > 0), t là thời gian tăng trưởng. Biết rằng số lượng vi khuẩn ban đầu là 100 con và sau 5 giờ có 300 con. Để số lượng vi khuẩn ban đầu sẽ tăng gấp đôi thì thời gian tăng trưởng t gần với kết quả nào sau đây nhất
A. 3 giờ 9 phút B. 3 giờ 2 phút. C. 3 giờ 16 phút. D.3 giờ 30 phút.
Lời giải:
Đáp án: A
Tỉ lệ tăng trưởng mỗi giờ của vi khuẩn là


Từ 100 con, để có 200 con ta có:
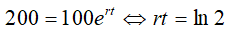
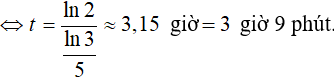
Ví dụ 7. Sự tăng trưởng của một loài vi khuẩn được tính theo công thức f(t) = A. er.t, trong đó A là số lượng vi khuẩn ban đầu, r là tỷ lệ tăng trưởng ( r > 0 ), t (tính theo giờ) là thời gian tăng trưởng. Biết số vi khuẩn ban đầu có 1000 con và sau 10 giờ là 5000 con. Hỏi sao bao lâu thì số lượng vi khuẩn tăng gấp 10 lần
A. 5ln 20 (giờ). B. 5 (giờ). C. 10log510 (giờ). D. 10log5 20 (giờ).
Lời giải:
Đáp án: C
Số vi khuẩn ban đầu có 1000 con và sau 10 giờ là 5000 con.
Áp dụng công thức f(t) = A. er.t, ta có 5000 = 1000e10r

Gọi t là thời gian cần tìm để số lượng vi khuẩn tăng gấp 10 lần.
Do đó:
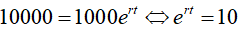

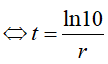

Ví dụ 8. Áp suất không khí P(đo bằng milimet thuỷ ngân, kí hiệu là mmHg) suy giảm mũ so với độ cao x( đo bằng mét), tức P giảm theo công thức P = P0. exi trong đó P0= 760mmHg là áp suất ở mực nước biển ( x=0), i là hệ số suy giảm. Biết rằng ở độ cao 1000m thì áp suất của không khí là 672,71mmHg . Hỏi áp suất không khí ở độ cao 3000 m gần với số nào sau đây nhất?
A.530,23mm Hg. B.540,23mmHg. C.520,23mmHg. D.510,23 mmHg
Lời giải:
Đáp án: A
Áp dụng công thức P = P0 exi
Ở độ cao 1000m ta có : P0 = 760mm Hg ; n=1000m ; P=672,71mmHg
Từ giả thiết này ta tìm được hệ số suy giảm i. Ta có

Khi đó ở độ cao 3000 m, áp suất của không khí là :
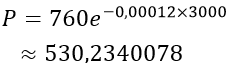
Ví dụ 9. Sự tăng trưởng của một loại vi khuẩn tuân theo công thức S= A.ert,trong đó A là số lượng vi khuẩn ban đầu, r là tỉ lệ tăng trưởng ( r>0 ), t là thời gian tăng trưởng. Biết rằng số lượng vi khuẩn ban đầu là 100 con và sau 5 giờ có 300 con. Để số lượng vi khuẩn ban đầu sẽ tăng gấp đôi thì thời gian tăng trưởng t gần với kết quả nào sau đây nhất.
A.3 giờ 9 phút. B.3 giờ 2 phút. C.3 giờ 16 phút. D.3 giờ 30 phút.
Lời giải:
Đáp án: A
Trước tiên, ta tìm tỉ lệ tăng trưởng mỗi giờ của loài vi khuẩn này.
Từ giả thiết: 300 = 100.e5r ⇔ e5r = 3

Tức là tỉ lệ tăng trưởng của loại vi khuẩn này là 21,97 % mỗi giờ.
Ta tìm thời gian để từ 100 con để có 200 con .
Từ công thức: 200= 100.ert ⇔ ert = 2
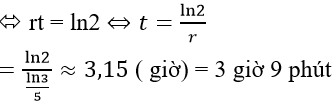
(199k) Xem Khóa học Toán 12 KNTTXem Khóa học Toán 12 CDXem Khóa học Toán 12 CTST
Xem thêm các dạng bài tập Toán lớp 12 ôn thi Tốt nghiệp có lời giải hay khác:
- Bài toán lãi đơn có lời giải
- Bài toán lãi kép có lời giải
- Bài toán Tiền gửi ngân hàng có lời giải
- Bài toán Gửi ngân hàng và rút tiền gửi hàng tháng có lời giải
- Bài toán Vay vốn trả góp có lời giải
- Bài tập lãi suất tổng hợp ôn thi Tốt nghiệp
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 12 Global Success
- Giải sgk Tiếng Anh 12 Smart World
- Giải sgk Tiếng Anh 12 Friends Global
- Lớp 12 Kết nối tri thức
- Soạn văn 12 (hay nhất) - KNTT
- Soạn văn 12 (ngắn nhất) - KNTT
- Giải sgk Toán 12 - KNTT
- Giải sgk Vật Lí 12 - KNTT
- Giải sgk Hóa học 12 - KNTT
- Giải sgk Sinh học 12 - KNTT
- Giải sgk Lịch Sử 12 - KNTT
- Giải sgk Địa Lí 12 - KNTT
- Giải sgk Giáo dục KTPL 12 - KNTT
- Giải sgk Tin học 12 - KNTT
- Giải sgk Công nghệ 12 - KNTT
- Giải sgk Hoạt động trải nghiệm 12 - KNTT
- Giải sgk Giáo dục quốc phòng 12 - KNTT
- Giải sgk Âm nhạc 12 - KNTT
- Giải sgk Mĩ thuật 12 - KNTT
- Lớp 12 Chân trời sáng tạo
- Soạn văn 12 (hay nhất) - CTST
- Soạn văn 12 (ngắn nhất) - CTST
- Giải sgk Toán 12 - CTST
- Giải sgk Vật Lí 12 - CTST
- Giải sgk Hóa học 12 - CTST
- Giải sgk Sinh học 12 - CTST
- Giải sgk Lịch Sử 12 - CTST
- Giải sgk Địa Lí 12 - CTST
- Giải sgk Giáo dục KTPL 12 - CTST
- Giải sgk Tin học 12 - CTST
- Giải sgk Hoạt động trải nghiệm 12 - CTST
- Giải sgk Âm nhạc 12 - CTST
- Lớp 12 Cánh diều
- Soạn văn 12 Cánh diều (hay nhất)
- Soạn văn 12 Cánh diều (ngắn nhất)
- Giải sgk Toán 12 Cánh diều
- Giải sgk Vật Lí 12 - Cánh diều
- Giải sgk Hóa học 12 - Cánh diều
- Giải sgk Sinh học 12 - Cánh diều
- Giải sgk Lịch Sử 12 - Cánh diều
- Giải sgk Địa Lí 12 - Cánh diều
- Giải sgk Giáo dục KTPL 12 - Cánh diều
- Giải sgk Tin học 12 - Cánh diều
- Giải sgk Công nghệ 12 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 12 - Cánh diều
- Giải sgk Giáo dục quốc phòng 12 - Cánh diều
- Giải sgk Âm nhạc 12 - Cánh diều




 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

