Dạng bài toán lãi kép ôn thi THPT Quốc gia có lời giải

Bài viết Dạng bài toán lãi kép ôn thi THPT Quốc gia với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập Dạng bài toán lãi kép ôn thi THPT Quốc gia.

Dạng bài toán lãi kép ôn thi THPT Quốc gia có lời giải

1. Phương pháp giải

- Định nghĩa

Lãi kép là nếu đến kì hạn người gửi không rút lãi ra thì tiền lãi được tính vào vốn của kì kế tiếp.

- Công thức tính

Khách hàng gửi vào ngân hàng A đồng với lãi kép r% /kì hạn thì số tiền khách hàng nhận được cả vốn lẫn lãi sau n kì hạn (n ∈ N*) là:

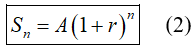
Chú ý: Từ công thức (2) ta có thể tính được:

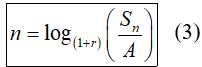
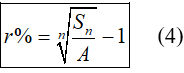
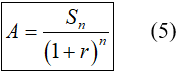
2. Ví dụ minh họa

Ví dụ 1. Chú Việt gửi vào ngân hàng 10 triệu đồng với lãi kép 5%/năm. Tính số tiền cả gốc lẫn lãi chú Việt nhận được sau khi gửi ngân hàng 10 năm (gần với số nào nhất)?

A. 16,234 triệu B. 16, 289 triệu C. 16, 327 triệu D.16, 280 triệu

Lời giải:

Đáp án: B

Số tiền cả gốc lẫn lãi nhận được sau 10 năm với lãi kép 5%/năm là

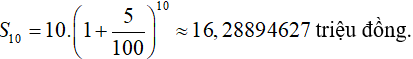
Ví dụ 2. Chú Việt gửi vào ngân hàng 10 triệu đồng .Với số tiền đó, nếu chú Việt gửi ngân hàng với lãi kép 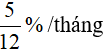thì sau 10 năm chú Việt nhận được bao nhiêu tiền?

A. 13,345 triệu B. 15,54 triệu C. 16,47 triệu D. 14,45 triệu

Lời giải:

Đáp án: C

10 năm = 12.10= 120 tháng.

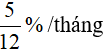
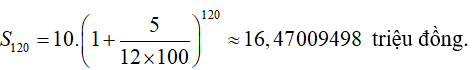
Số tiền cả gốc lẫn lãi nhận được sau 10 năm với lãi kép là

Ví dụ 3. Bạn An gửi tiết kiệm một số tiền ban đầu là 1000000 đồng với lãi suất 0,58%/tháng (không kỳ hạn). Hỏi bạn An phải gửi bao nhiêu tháng thì được cả vốn lẫn lãi bằng hoặc vượt quá 1300000 đồng ?

A. 46 tháng B. 44 tháng C. 45 tháng D. 47 tháng

Lời giải:

Đáp án: A

Áp dụng công thức ( 3) ta có số kì hạn là:

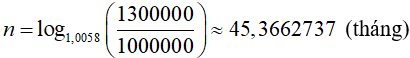
Nên để nhận được số tiền cả vốn lẫn lãi bằng hoặc vượt quá 1300000 đồng thì bạn An phải gửi ít nhất là 46 tháng.

Ví dụ 4. Lãi suất của tiền gửi tiết kiệm của một số ngân hàng thời gian vừa qua liên tục thay đổi. Bạn Châu gửi số tiền ban đầu là 5 triệu đồng với lãi suất 0,7% tháng chưa đầy một năm, thì lãi suất tăng lên 1,15% tháng trong nửa năm tiếp theo và bạn Châu tiếp tục gửi; sau nửa năm đó lãi suất giảm xuống còn 0,9% tháng, bạn Châu tiếp tục gửi thêm một số tháng tròn nữa, khi rút tiền bạn Châu được cả vốn lẫn lãi là 5 747 478,359 đồng (chưa làm tròn). Hỏi bạn Châu đã gửi tiền tiết kiệm trong bao nhiêu tháng?

A. 10 tháng B. 12 tháng C. 14 tháng D.15 tháng

Lời giải:

Đáp án: D

Gọi X; Y (X, Y ∈ Z⁺: X, Y ≤ 12) lần lượt là số tháng bạn Châu đã gửi với lãi suất 0,7%/tháng và 0,9%/tháng . Theo công thức lãi kép, ta có số tiền bạn Châu thu được cuối cùng là:

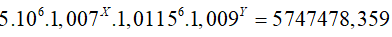
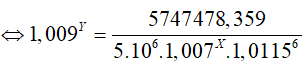
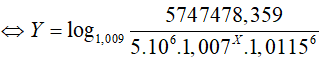
Kết hợp điều kiện; X và Y nguyên dương ta thấy X= 5 và Y= 4 thỏa mãn.

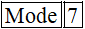
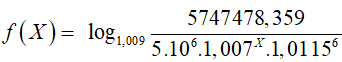
(Nhập vào máy tính nhập hàm số , cho giá trị X chạy từ 1 đến 10 với STEP 1. Nhìn vào bảng kết quả ta được cặp số nguyên là X= 5;Y= 4).

Vậy bạn Châu đã gửi tiền tiết kiệm trong: 5+6+ 4= 15 tháng.

Ví dụ 5. Bà Mai gửi tiết kiệm ngân hàng Vietcombank số tiền 50 triệu đồng với lãi suất 0,79% một tháng, theo phương thức lãi kép. Tính số tiền cả vốn lẫn lãi bà Mai nhận được sau 2 năm? (làm tròn đến hàng nghìn)

A. 60 393 000. B. 50 793 000 C. 50 790 000. D. 59 480 000

Lời giải:

Đáp án: A

Đây là bài toán lãi kép với chu kỳ là một tháng, ta áp dụng công thức A( 1+ r)n với A = 50 triệu đồng, r% = 0, 79% và n= 2.12 = 24 tháng.

Ta được: S= 50.(1+ 0,0079 )²⁴ ≈ 60,393 triệu đồng

Ví dụ 6. Chị Thanh gửi ngân hàng 155 triệu đồng, với lãi suất 1,02 % một quý. Hỏi sau một năm số tiền lãi chị nhận được là bao nhiêu? (làm tròn đến hàng nghìn)

A. 161 421 000. B. 161 324 000 C. 7 698 000 D. 6 421 000

Lời giải:

Đáp án: D

Số tiền lãi chính là tổng số tiền cả gốc lẫn lãi trừ đi số tiền gốc.

Áp dụng công thức lãi kép với 12 tháng= 4 quý (n = 4) nên số tiền lãi là 155.(1 + 0,0102)⁴ − 155 ≈ 6421000 (đồng).

Ví dụ 7. Anh Thành trúng vé số giải thưởng 125 triệu đồng, sau khi trích ra 20% số tiền để chiêu đãi bạn bè và làm từ thiện, anh gửi số tiền còn lại vào ngân hàng với lãi suất 0, 31% một tháng. Dự kiến 10 năm sau, anh rút tiền cả vốn lẫn lãi cho con gái vào đại học. Hỏi khi đó anh Thành rút được bao nhiêu tiền? (làm tròn đến hàng nghìn)

A.144 980 000. B. 103 144 000 C. 182 650 000. D. 138 650 000

Lời giải:

Đáp án: A

Số tiền anh Thành gửi vào ngân hàng là 125. 80% = 100 (triệu đồng).

Áp dụng công thức lãi kép, sau 10 năm là tháng, số tiền nhận được cả vốn lẫn lãi là:

100(1 + 0,0031)¹²⁰ ≈ 144,98 (triệu đồng).

Ví dụ 8. Một khách hàng gửi ngân hàng 20 triệu đồng, kỳ hạn 3 tháng, với lãi suất 0,65 % một tháng theo phương thức lãi kép. Hỏi sau bao lâu vị khách này mới có số tiền lãi nhiều hơn số tiền gốc ban đầu gửi ngân hàng? Giả sử người đó không rút lãi ở tất cả các định kỳ.

A. 8 năm 11 tháng. B. 19 tháng. C. 18 tháng. D. 9 năm.

Lời giải:

Đáp án: D

Lãi suất theo kỳ hạn 3 tháng là 3. 0,65 %= 1,95 %

Gọi n là số kỳ hạn cần tìm. Theo giả thiết ta có n là số tự nhiên nhỏ nhất thỏa mãn:

20. (1+ 0,0195)ⁿ − 20 > 20

Ta được n= 36 chu kỳ, một chu kỳ là 3 tháng.

Nên thời gian cần tìm là 36. 3= 108 tháng = 9 năm.

Ví dụ 9. Một khách hàng gửi ngân hàng 20 triệu đồng, kỳ hạn 3 tháng, với lãi suất 0,65 % một tháng theo phương thức lãi kép. Hỏi sau bao lâu vị khách này mới có số tiền lãi nhiều hơn số tiền gốc ban đầu gửi ngân hàng? Giả sử người đó không rút lãi ở tất cả các định kỳ.

A. 8 năm 11 tháng. B.19 tháng. C. 18 tháng. D.9 năm.

Lời giải:

Đáp án: D

Lãi suất theo kỳ hạn 3 tháng là 3. 0,65 % = 1,95%

Gọi n là số kỳ hạn cần tìm.

Đến tháng thứ n số tiền người đó có ( kể cả gốc lẫn lãi) là: S_n = 20. (1+ 0,0195)ⁿ ( triệu đồng).

Do số tiền gốc là 20 triệu đồng nên số tiền lãi có được khi đó là:

20. (1 + 0,0195)ⁿ − 20 ( triệu đồng).

Theo giả thiết ta có n là số tự nhiên nhỏ nhất thỏa mãn:

20. (1+ 0,0195)n − 20 > 20

Giải ra ta được, n = 36 chu kỳ, một chu kỳ là 3 tháng, nên thời gian cần tìm là 36 .3 = 108 tháng, tức là 9 năm.

Ví dụ 10. Tính đến đầu năm 2011, dân số toàn tỉnh Bình Phước đạt gần 905 300, mức tăng dân số là 1,37% mỗi năm. Tỉnh thực hiện tốt chủ trương 100% trẻ em đúng độ tuổi đều vào lớp 1. Đến năm học 2024-2025 ngành giáo dục của tỉnh cần chuẩn bị bao nhiêu phòng học cho học sinh lớp 1, mỗi phòng dành cho 35 học sinh? ( Giả sử trong năm sinh của lứa học sinh vào lớp 1 đó toàn tỉnh có 2400 người chết, số trẻ tử vong trước 6 tuổi không đáng kể)

A.458. B. 459. C. 419. D. 221.

Lời giải:

Đáp án: B

Chỉ những em sinh năm 2018 mới đủ tuổi đi học (6 tuổi) vào lớp 1 năm học 2024-2025.

Áp dụng công thức lãi kép: S_n = A. (1+ r)ⁿ để tính dân số năm 2018.

Trong đó: A= 905 300 ; r= 1,37 %= 0,0137 và n= ( 2018 – 2011 ) + 1= 8 năm

Dân số năm 2018 là:

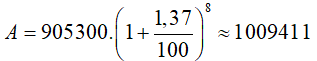
Dân số năm 2017 là:

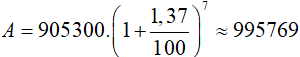
Số trẻ vào lớp 1 là: 1009411 − 995769 + 2400 = 16042 (người)

Số phòng học cần chuẩn bị là : 16042:35 ≈ 458,3428571 (phòng)

Do đó, ngành giáo dục cần chuẩn bị 459 phòng.

Ví dụ 11. Tính đến đầu năm 2011, toàn tỉnh Long An có 1 691 400 người, đến đầu năm 2015 dân số của tỉnh Long An sẽ là 1 802 500 người. Hỏi trung bình mỗi năm dân số của tỉnh Long An tăng bao nhiêu phần trăm?

A. 1,6%. B.1,3%. C.1,2%. D.16,4%.

Lời giải:

Đáp án: B

Áp dụng công thức lãi suất kép ta có : S_n = A. (1+ r)ⁿ. Do đó :

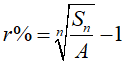
Trong đó: A= 1 691 400 ; S_n =1 802 500 và n= 2015 − 2011 = 4 năm.

Suy ra,trung bình mỗi năm dân số của tỉnh Long An tăng số phần trăm là :

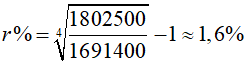
Ví dụ 12. Ông Năm gửi 320 triệu đồng ở hai ngân hàng X và Y theo phương thức lãi kép. Số tiền thứ nhất gửi ở ngân hàng X với lãi suất 2,1% một quý trong thời gian 15 tháng. Số tiền còn lại gửi ở ngân hàng Y với lãi suất 0,73% một tháng trong thời gian 9 tháng. Tổng lợi tức đạt được ở hai ngân hàng là 27 507 768,13 đồng. Hỏi số tiền ông Năm lần lượt gửi ở ngân hàng X và Y là bao nhiêu?

A. 140 triệu và 180 triệu. B.180 triệu và 140 triệu.

C. 200 triệu và 120 triệu. D. 120 triệu và 200 triệu.

Lời giải:

Đáp án: A

Tổng số tiền cả vốn và lãi (lãi chính là lợi tức) ông Năm nhận được từ cả hai ngân hàng là :

320 000 000 + 27 507 768,13 = 347 507 768,13 đồng = 347, 50776813 triệu đồng.

Gọi x (triệu đồng) là số tiền gửi ở ngân hàng X, khi đó 320 − x (triệu đồng) là số tiền gửi ở ngân hàng Y.

Số tiền ông Năm có được ( cả gốc lẫn lãi) ở ngân hàng X trong 15 tháng = 5 quý là :

x.(1+ 0,021)⁵ triệu đồng.

Số tiền ông Năm có được ( cả gốc lẫn lãi) ở ngân hàng Y trong 9 tháng là :

(320 − x).(1+ 0,0073)⁹ triệu đồng

Theo giả thiết ta có: x.(1+ 0,021)5 + ( 320 − x) . (1 + 0,0073)⁹ = 347, 50776813

Giải ra, ta được x= 140.

Vậy ông Năm gửi 140 triệu ở ngân hàng X và 180 triệu ở ngân hàng Y.

3. Bài tập tự luyện

Bài 1. Sau một thời gian làm việc, chị An có số vốn là 450 triệu đồng. Chị An chia số tiền thành hai phần và gửi ở hai ngân hàng Agribank và Sacombank theo phương thức lãi kép. Số tiền ở phần thứ nhất chị An gửi ở ngân hàng Agribank với lãi suất 2,1% một quý trong thời gian 18 tháng. Số tiền ở phần thứ hai chị An gửi ở ngân hàng Sacombank vớ i lãi suất 0,73% một tháng trong thời gian 10 tháng. Tổng s ố tiền lãi thu được ở hai ngân hàng là 50,01059203 triệu đồng. Hỏi số tiền chị An đã gửi ở mỗi ngân hàng Agribank và Sacombank là bao nhiêu?

Bài 2. Bạn An gửi tiết kiệm vào ngân hàng với số tiền là 1.000.000 đồng không kì hạn với lãi suất là 0,65% mỗi tháng. Tính số tiền bạn An nhận được sau 2 năm?

Bài 3. Một người gửi số tiền 500 (triệu đồng) vào ngân hàng với lãi suất 6,5/năm theo hình thức lãi kép. Đến hết năm thứ 3, vì cần tiền nên người đó rút ra 100 (triệu đồng), phần còn lại vẫn tiếp tục gửi. Hỏi sau 5 năm kể từ lúc bắt đầu gửi, người đó có được số tiền là bao nhiêu? (Giả sử lãi suất không thay đổi trong suốt quá trình gửi; không kể 100 (triệu đồng) đã rút).

Bài 4. Theo hình thức lãi kép, một người gửi vào ngân hàng 15 triệu đồng, lãi suất theo kì hạn 1 năm là 6%. Hỏi sau ít nhất bao nhiêu năm thì số tiền người này thu về ít nhất là 19 triệu đồng?

Bài 5. Theo hình thức lãi kép, một người gửi vào ngân hàng 10 triệu đồng, lãi suất theo kì hạn 1 tháng là 0,5%. Tính số tiền lãi người này thu về sau 2 năm.

Bài 6. Theo hình thức lãi kép, một người gửi vào ngân hàng 10 triệu đồng, lãi suất theo kì hạn 1 năm là 6%. Tính số tiền lãi người này thu về sau 2 năm.

Bài 7. Bạn Lan muốn có 10.000.000 đồng sau 15 tháng thì mỗi tháng phải gửi vào ngân hàng bao nhiêu tiền, biết lãi suất ngân hàng là 0,6% mỗi tháng.

Bài 8. Một người lần đầu gửi vào ngân hàng 100triệu đồng với kì hạn 3 tháng, lãi suất 2% một quý theo hình thức lãi kép. Sau đúng 6 tháng, người đó gửi thêm 100 triệu đồng với kì hạn và lãi suất như trước đó. Tổng số tiền người đó nhận được sau 1 năm gửi thêm tiền?

Bài 9. Ông An gửi 320 triệu đồng vào ngân hàng ACB và VietinBank theo phương thức lãi kép. Số tiền thứ nhất gửi vào ngân hàng ACB với lãi suất 2,1% một quý trong thời gian 15 tháng. Số tiền còn lại gửi vào ngân hàng VietinBank với lãi suất 0,73% một tháng trong thời gian 9 tháng. Biết tổng số tiền lãi ông An nhận được ở hai ngân hàng là 26670725,95 đồng. Hỏi số tiền ông An lần lượt ở hai ngân hàng ACB và VietinBank là bao nhiêu (số tiền được làm tròn tới hàng đơn vị)?

Bài 10. Thầy C gửi 5 triệu đồng vào ngân hàng với lãi suất 0,7%/tháng. Chưa đầy một năm thì lãi suất tăng lên thành 1,15%/tháng. Tiếp theo, sáu tháng sau lãi suất chỉ còn 0,9%/tháng. Thầy C tiếp tục gửi thêm một số tháng nữa rồi rút cả vỗn lẫn lãi được 5787710,707 đồng. Hỏi thầy C đã gửi tổng thời gian bao nhiêu tháng?

Xem thêm các dạng bài tập Toán lớp 12 có trong đề thi THPT Quốc gia khác:

• Dạng bài toán lãi đơn có lời giải
• Dạng bài toán Tiền gửi ngân hàng có lời giải
• Dạng bài toán Gửi ngân hàng và rút tiền gửi hàng tháng có lời giải
• Dạng bài toán Vay vốn trả góp có lời giải
• Dạng bài toán Lãi kép liên tục có lời giải
• Các dạng bài toán lãi suất hay có lời giải

---