Phương pháp giải bài toán bằng cách lập hệ phương trình siêu lớp 9 (hay, chi tiết)
Bài viết Phương pháp giải bài toán bằng cách lập hệ phương trình lớp 9 với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập Phương pháp giải bài toán bằng cách lập hệ phương trình.
Phương pháp giải bài toán bằng cách lập hệ phương trình siêu hay, chi tiết
(199k) Xem Khóa học Toán 9 KNTTXem Khóa học Toán 9 CDXem Khóa học Toán 9 CTST
A. Phương pháp giải
Bước 1: Lập hệ phương trình:
+ Đặt ẩn và tìm điều kiện của ẩn (nếu có).
+ Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.
+ Lập hệ phương trình biểu diễn tương quan giữa các đại lượng.
Bước 2: Giải hệ phương trình.
Bước 3: So sánh với điều kiện và kết luận.
B. Ví dụ minh họa
Ví dụ 1: Tìm số có hai chữ số biết chữ số ở hàng chục lớn hơn chữ số hàng đơn vị là 2. Số đó gấp 7 lần tổng hai chữ số của nó.
Hướng dẫn giải:
Gọi số cần tìm là với
Vì chữ số ở hàng chục lớn hơn chữ số hàng đơn vị là 2, nên ta có: a – b = 2
Vì số đó gấp 7 lần tổng hai chữ số của nó, nên ta có: 10a + b = 7(a + b)
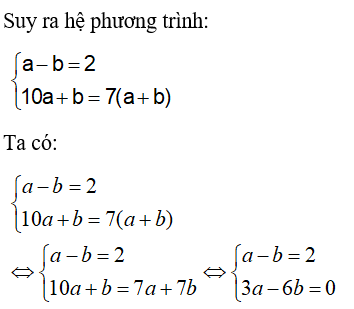
Nhân pt (1) với 3 ta được: 3a – 3b = 6 (3)
Lấy pt (3) – pt (2) ta được: 3b = 6 ⇔ b = 2 ( tm )
Với b = 2 ⇒ a = 4 ( tm)
Vậy số cần tìm là: 42.
Ví dụ 2: Hai vật chuyển động đều trên một đường tròn đường kính 20cm, xuất phát cùng một lúc, từ một điểm, nếu chuyển động cùng chiều cứ 20 giây chúng lại gặp nhau, nếu chuyển động ngược chiều thì cứ 4 giây chúng lại gặp nhau. Tìm vận tốc của mỗi vật.
Hướng dẫn giải:
Gọi vận tốc của hai vật lần lượt là x (cm/s) và y (cm/s). ( x , y > 0, giả sử x > y)
Vì nếu chuyển động cùng chiều cứ 20 giây chúng lại gặp nhau nên hiệu quãng đường đi được trong 20 giây của hai vật là chu vi của đường tròn, do đó: 20x – 20y = 20π
Vì nếu chuyển động ngược chiều thì cứ 4 giây chúng lại gặp nhau nên tổng quãng đường đi được trong 4 giây của hai vật là chu vi của đường tròn, do đó: 4x + 4y = 20 π
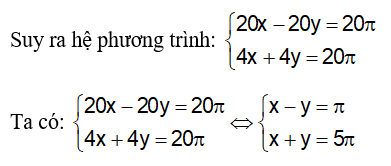
Cộng vế theo vế của hai phương trình trên ta được: 2x=6π ⇔ x =3π ( tm)
Với x=3π ⇒ y = 5π-3π = 2π (tm)
Vậy vận tốc của hai vật lần lượt là: 3π(cm/s),2π(cm/s)
Ví dụ 3: Hai người thợ cùng làm chung một công việc trong 16 giờ thi xong. Nếu người thứ nhất làm trong 3 giờ và người thứ hai làm trong 6 giờ thì được 25% khối lượng cộng việc. Hỏi mỗi người làm một mình thì hết bao lâu?
Hướng dẫn giải:
Gọi thời gian để người thứ nhất làm xong công việc đó là x (giờ), ( x > 16)
Gọi thời gian để người thứ hai làm xong công việc đó là y (giờ), ( y > 16)
Vì hai người cùng làm chung công việc trong 16 giờ thi xong, nên ta có: 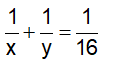
Vì người thứ nhất làm trong 3 giờ và người thứ hai làm trong 6 giờ thì được 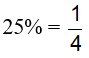
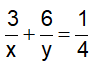
Nhân pt(1) với 3 ta được: 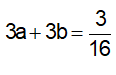
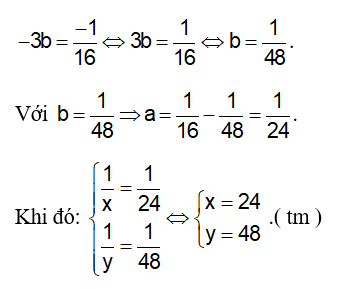
Vậy người thứ nhất làm hết 24 giờ, người thứ hai làm hết 48 giờ.
C. Bài tập trắc nghiệm
Câu 1: Hai đội cùng làm chung một công việc và dự định xong trong 12 ngày thi xong. Họ cùng làm trong 8 ngày, thì đội I được điều đi làm việc khác, đội II làm tiếp. Do cải tiến kỹ thuật năng suất tăng lên gấp đôi nên đội II làm xong cộng việc còn lại trong 3,5 ngày. Hỏi mỗi đội làm một mình thì hết bao lâu?
A. Đội I: 28 ngày và Đội II: 21 ngày
B. Đội I: 28 ngày và Đội II: 24 ngày
C. Đội I: 21 ngày và Đội II: 28 ngày
D. Đội I: 24 ngày và Đội II: 21 ngày
Lời giải:
Đáp án: A
Gọi thời gian để đội I làm xong công việc đó là x (giờ), ( x > 12)
Gọi thời gian để đội II làm xong công việc đó là y (giờ), ( y > 12)
Vì hai đội cùng làm chung dự định xong trong 12 ngày thi xong, nên ta có:
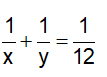
Đội II phải làm khối lượng công việc còn lại là:
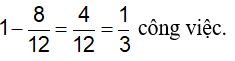
Vì cải tiến kỹ thuật năng suất tăng lên gấp đôi nên đội II làm xong cộng việc còn lại trong 3,5 ngày, nên ta có:
Vậy đội I làm trong 28 ngày, đội II làm trong 21 ngày.
Câu 2: Tìm hai số biết tổng của hai số đó bằng 19, tổng các bình phương của hai số đó bằng 185.( biết hai số đó là số nguyên)
A. 11 và 9 hoặc 9 và 11
B. 11 và 8 hoặc 8 và 11
C. 8 và 12 hoặc 12 và 8
D. 10 và 11 hoặc 11 và 10
Lời giải:
Đáp án: B
Gọi hai số cần tìm lần lượt là x và y (x,y ∈ Z )
Vì tổng của hai số đó bằng 19, nên ta có: x + y = 19
Vì tổng các bình phương của hai số đó bằng 185, nên ta có: x2 + y2 = 185

Vậy hai số cần tìm là 11 và 8 (hoặc 8 và 11).
Câu 3: Hai vòi nước cùng chảy vào một bể trong 1 giờ 20 phút thì đầy bể. Nếu mở vòi thứ nhất chảy trong 10 phút và mở vòi thứ hai chảy trong 12 phút thì được 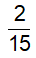
A. vòi thứ nhất : 220 phút và vòi thứ hai: 240 phút.
B. vòi thứ nhất : 120 phút và vòi thứ hai: 140 phút.
C. vòi thứ nhất : 120 phút và vòi thứ hai: 240 phút.
D. vòi thứ nhất : 240 phút và vòi thứ hai: 120 phút.
Lời giải:
Đáp án: c
Đổi 1 giờ 20 phút = 80 phút.
Gọi thời gian để vòi thứ nhất chảy một mình để bể là x (phút), ( x > 80)
Gọi thời gian để vòi thứ hai chảy một mình để bể là y (phút), ( y > 80)
Vì hai vòi nước cùng chảy vào một bể trong 1 giờ 20 phút thì đầy bể, nên ta có: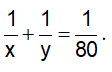 Vì mở vòi thứ nhất chảy trong 10 phút và mở vòi thứ hai chảy trong 12 phút thì được
Vì mở vòi thứ nhất chảy trong 10 phút và mở vòi thứ hai chảy trong 12 phút thì được 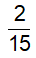 bể, ta có: .
bể, ta có: .
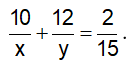
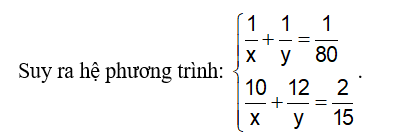
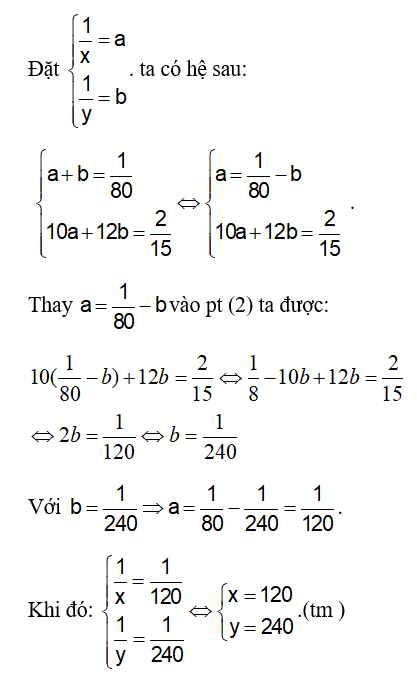
Câu 4: Tìm hai số biết tổng của chúng là 1006, nếu lấy số lớn chia cho số bé thì được thương là 2 và số dư là 124. ( biết hai số đó là số nguyên dương)
A. số lớn: 712 và số bé : 294
B. số lớn: 702 và số bé : 304
C. số lớn: 612 và số bé : 394
D. số lớn: 512 và số bé : 494
Lời giải:
Đáp án: A
Gọi hai số cần tìm lần lượt là x, y ( x > y, 0 < x, y < 1006 )
Vì tổng của hai số là 1006, nên ta có: x + y = 1006
Vì số lớn chia cho số bé thì được thương là 2 và số dư là 124, nên ta có: x = 2y +124
Suy ra hệ phương trình:
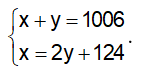
Thay x = 2y + 124 vào pt (1) ta được: 2y + 124 + y = 1006 ⇔ 3y = 882 ⇔ y = 294 ( tm )
Với y = 294 ⇒ x = 2.294 + 124 = 712 ( tm )
Vậy hai số cần tìm là: 712 và 294.
Câu 5: Một thửa ruộng hình chữ nhật có chiều rộng ngắn hơn chiều dài 45m. Tính diện tích của thửa ruộng, biết nếu giảm chiều dài 2 lần và tăng chiều rộng lên 3 lần thì chu vi không đổi.
A, 640 m2
B, 600 m2
C, 800 m2
D, 900 m2
Lời giải:
Đáp án: D
Gọi chiều dài của thửa ruộng là x (m), ( x > 45)
Gọi chiều rộng của thửa ruộng là y (m) ( 0 < y < x)
Vì thửa ruộng hình chữ nhật có chiều rộng ngắn hơn chiều dài 45m, nên ta có: x – y = 45
Vì nếu giảm chiều dài 2 lần và tăng chiều rộng lên 3 lần thì chu vi không đổi, ta có:
2(0,5x + 3y) = 2(x + y) ⇔ 0,5x + 3y = x + y
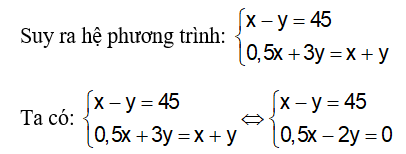
Nhân pt (1) với 2 ta được: 2x – 2y = 90, rồi trừ vế với vế cho pt (2) ta được:
1,5x = 90 ⇔ x = 60 (tm )
Với x = 60 ⇒ y = 60 – 45 = 15 ( tm )
Vậy diện tích của thửa ruộng là: 60 . 15 = 900 m2.
Câu 6: Một hình chữ nhật có chu vi là 70m, nếu giảm chiều rộng 3m và tăng chiều dài lên 5m thì diện không đổi. Tìm chiều rộng và chiều dài?
A. chiều rộng: 15m và chiều dài : 20m
B. chiều rộng: 10m và chiều dài : 25m
C. chiều rộng: 25m và chiều dài : 10m
D. chiều rộng: 5m và chiều dài : 30m
Lời giải:
Đáp án: A
Gọi chiều rộng của hình chữ nhật là x (m), ( 0 < x < 35)
Gọi chiều dài của hình nhật là y (m), ( x <y < 35)
Vì chu vi của hình chữ nhật la 70m, ta có: 2( x + y) = 70 ⇔ x + y = 35
Vì giảm chiều rộng 3m và tăng chiều dài lên 5m thì diện không đổi, ta có: (x – 3)(y + 5) = xy
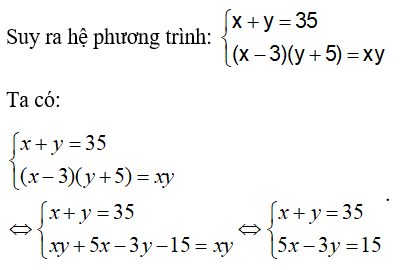
Từ pt (1) suy ra: x = 35 – y, thay vào pt (2) ta được:
5(35 – y) – 3y = 15 ⇔ 175 – 5y – 3y = 15 ⇔ 8y = 160 ⇔ y = 20 ( tm )
Với y = 20 ⇒ x = 35 – 20 = 15 ( tm )
Vậy chiều rộng của hình chữ nhật là: 15m và chiều dài là: 20m.
Câu 7: Ở nông trường, có hai máy cày cùng cày trên thửa ruộng hết 2 giờ thì xong, nếu mỗi máy cày riệng thửa ruộng đó thì máy cày thứ 1 cày xong sớm hơn máy cày thứ 2 là 3 giờ. Tính thời gian mỗi máy cày làm việc riêng?
A. máy 1 là: 4 giờ và máy 2 là: 7 giờ.
B. máy 1 là: 3 giờ và máy 2 là: 6 giờ.
C. máy 1 là: 2 giờ và máy 2 là: 5 giờ.
D. máy 1 là: 5 giờ và máy 2 là: 8 giờ.
Lời giải:
Đáp án: B
Gọi thời gian máy cày thứ nhất làm riêng là x (giờ), ( x > 2)
Gọi thời gian máy cày thứ hai làm riêng là y (giờ), ( y > 3)
Trong 1 giờ cả hai máy cày được là :
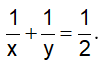
Vì khi làm riêng thì máy thứ nhất làm xong sớm hơn máy thứ hai là 3 giờ, nên ta có: y = x + 3
Suy ra hệ phương trình:
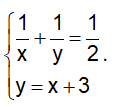
Thay y = x + 3 vào pt (1) ta được:
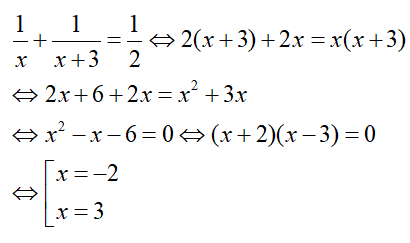
Với x = –2 ( loại)
Với x = 3 => y = 6 ( tm )
Vậy máy cày thứ làm hết: 3 giờ, máy cày thứ hai làm hết : 6 giờ.
Câu 8: Một người mua hai mặt hàng A và B. Nếu tăng giá mặt hàng A thêm 10% và tăng thêm giá mặt hàng B thêm 20% thì người đó phải trả 232 nghìn đồng, nếu giảm giá cả hai mặt hàng 10% thì người đó phải trả 180 nghìn đồng. Tính giá tiền mỗi loại.
A. mặt hàng A: 60 nghìn đồng và mặt hàng B: 100 nghìn đồng.
B. mặt hàng A: 70 nghìn đồng và mặt hàng B: 90 nghìn đồng.
C. mặt hàng A: 80 nghìn đồng và mặt hàng B: 120 nghìn đồng.
D. mặt hàng A: 80 nghìn đồng và mặt hàng B: 100 nghìn đồng.
Lời giải:
Đáp án: C
Gọi giá tiền của mặt hàng thứ A là x (nghìn đồng), ( x > 0)
Gọi giá tiền của mặt hàng thứ B là y (nghìn đồng), ( y > 0)
Vì tăng giá mặt hàng A thêm 10% và tăng thêm giá mặt hàng B thêm 20% thì người đó phải trả 232 nghìn đồng, nên ta có: 1,1x + 1,2y = 232.
Vì giảm giá cả hai mặt hàng 10% thì người đó phải trả 180 nghìn đồng,ta có: 0,9x + 0,9y = 180
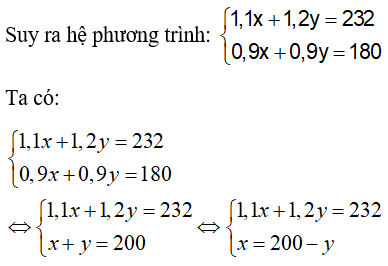
Thay x = 200 – y vào pt (1) ta được:
1,1(200-y) + 1,2y = 232 ⇔ 220 - 1,1y + 1,2y = 232 ⇔ 0,1y = 12 ⇔ y =120.( tm )
Với y = 120 => x = 80 ( tm )
Vậy giá mặt hàng A: 80 nghìn đồng, giá tiền mặt hàng B: 120 nghìn đồng.
Câu 9: Hai trường A và B của một thị trấn có 210 học sinh thi đỗ vào lớp 10,tỷ lệ trúng tuyển là 84%. Tính riêng thì trường A có 80% học sinh thi đỗ và trường B có 90% học sinh thi đỗ. Hỏi mỗi trường có bao nhiêu học sinh dự thi vào lớp 10.
A. trường A: 150 học sinh và trường B: 100 học sinh.
B. trường A: 110 học sinh và trường B: 140 học sinh.
C. trường A: 120 học sinh và trường B: 130 học sinh.
D. trường A: 100 học sinh và trường B: 150 học sinh.
Lời giải:
Đáp án: A
Gọi số học sinh của trương A tham gia thi vào lớp 10 là x (học sinh), ( 0 < x < 210, x ∈ z+ )
Gọi số học sinh của trương B tham gia thi vào lớp 10 là y (học sinh), ( 0 < y < 210, y ∈ z+ )
Tổng số học sinh của hai trường tham gia thi vào lớp 10 là: 210 : 84% = 250 ( học sinh)
Ta có: x + y = 250
Vì trường A có 80% học sinh thi đỗ và trường B có 90% học sinh thi đỗ, ta có:
0,8x + 0,9y = 210
Suy ra hệ phương trình:
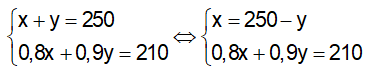
Thay x = 250 – y vào pt (2) ta được:
0,8(250 – y) + 0,9y = 210 ⇔ 200 – 0,8y + 0,9y = 210 ⇔ 0,1y = 100 ⇔ y = 100 ( tm )
Với y = 100 => x = 250 – 100 = 150 ( tm )
Vậy trường A có 150 học sinh, trường B có 100 học sinh.
Câu 10: Một thửa đất hình chữ nhật có chu vi là 198m và diện tích là 2430 m2. Tính chiều dài và chiều rộng của thửa đất đó?
A. chiều dài : 53m và chiều rộng: 46m
B. chiều dài : 59m và chiều rộng: 40m
C. chiều dài : 57m và chiều rộng: 42m
D. chiều dài : 54m và chiều rộng: 45m
Lời giải:
Đáp án: D
Gọi chiều dài của thửa đất là x (m), ( 0 < x < 99)
Gọi chiều rộng của thửa đát là y(m), ( 0 < y < 99, y < x)
Vì thửa đất có chu vi là 198m , nên ta có: 2(x + y) = 198 ⇔ x + y = 99
Vì thửa đất có diện tích là 2430m2, nên ta có: xy = 2430

Vậy chiều dài của thửa đất : 54m, chiều rộng thửa đất: 45m.
(199k) Xem Khóa học Toán 9 KNTTXem Khóa học Toán 9 CDXem Khóa học Toán 9 CTST
Xem thêm các dạng bài tập Toán lớp 9 chọn lọc, có đáp án chi tiết hay khác:
Tủ sách VIETJACK luyện thi vào 10 cho 2k11 (2026):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Loạt bài Chuyên đề: Lý thuyết - Bài tập Toán lớp 9 Đại số và Hình học có đáp án có đầy đủ Lý thuyết và các dạng bài được biên soạn bám sát nội dung chương trình sgk Đại số 9 và Hình học 9.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 9 Global Success
- Giải sgk Tiếng Anh 9 Smart World
- Giải sgk Tiếng Anh 9 Friends plus
- Lớp 9 Kết nối tri thức
- Soạn văn 9 (hay nhất) - KNTT
- Soạn văn 9 (ngắn nhất) - KNTT
- Giải sgk Toán 9 - KNTT
- Giải sgk Khoa học tự nhiên 9 - KNTT
- Giải sgk Lịch Sử 9 - KNTT
- Giải sgk Địa Lí 9 - KNTT
- Giải sgk Giáo dục công dân 9 - KNTT
- Giải sgk Tin học 9 - KNTT
- Giải sgk Công nghệ 9 - KNTT
- Giải sgk Hoạt động trải nghiệm 9 - KNTT
- Giải sgk Âm nhạc 9 - KNTT
- Giải sgk Mĩ thuật 9 - KNTT
- Lớp 9 Chân trời sáng tạo
- Soạn văn 9 (hay nhất) - CTST
- Soạn văn 9 (ngắn nhất) - CTST
- Giải sgk Toán 9 - CTST
- Giải sgk Khoa học tự nhiên 9 - CTST
- Giải sgk Lịch Sử 9 - CTST
- Giải sgk Địa Lí 9 - CTST
- Giải sgk Giáo dục công dân 9 - CTST
- Giải sgk Tin học 9 - CTST
- Giải sgk Công nghệ 9 - CTST
- Giải sgk Hoạt động trải nghiệm 9 - CTST
- Giải sgk Âm nhạc 9 - CTST
- Giải sgk Mĩ thuật 9 - CTST
- Lớp 9 Cánh diều
- Soạn văn 9 Cánh diều (hay nhất)
- Soạn văn 9 Cánh diều (ngắn nhất)
- Giải sgk Toán 9 - Cánh diều
- Giải sgk Khoa học tự nhiên 9 - Cánh diều
- Giải sgk Lịch Sử 9 - Cánh diều
- Giải sgk Địa Lí 9 - Cánh diều
- Giải sgk Giáo dục công dân 9 - Cánh diều
- Giải sgk Tin học 9 - Cánh diều
- Giải sgk Công nghệ 9 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 9 - Cánh diều
- Giải sgk Âm nhạc 9 - Cánh diều
- Giải sgk Mĩ thuật 9 - Cánh diều

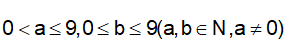
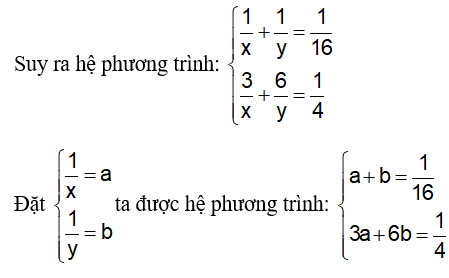
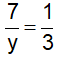




 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

