200+ Trắc nghiệm Giải tích 2 (có đáp án)
Tổng hợp trên 200 câu hỏi trắc nghiệm Giải tích 2 có đáp án với các câu hỏi đa dạng, phong phú từ nhiều nguồn
giúp sinh viên ôn trắc nghiệm Giải tích 2 đạt kết quả cao.
200+ Trắc nghiệm Giải tích 2 (có đáp án)
Quảng cáo
I. Bài tập trắc nghiệm Tích phân Euler
Câu 1 : Kết quả của tích phân ∫ 0 + ∞ x 5 e - x 4 dx
A. π 8
B. π 2
C. π 6
D. π 6
Hiển thị đáp án
Chọn đáp án A
Giải thích:
Đặt
⇒ ∫ 0 + ∞ x 5 e - x 4 dx = 1 4 ∫ 0 + ∞ u 1 2 e - u du = 1 4 ∫ 0 + ∞ u 3 2 - 1 e - u du = 1 4 Γ ( 3 2 ) = π 8
Câu 2 : Kết quả của tích phân ∫ 0 π 2 sin 6 x c o s 4 x dx
A. 7 π 512
B. 2 π 512
C. π 512
D. 3 π 512
Hiển thị đáp án
Chọn đáp án D
Giải thích:
∫ 0 π 2 sin 6 x c o s 4 x dx = ∫ 0 π 2 ( sin x ) 2 . 7 2 - 1 ( c o s x ) 2 . 5 2 - 1 dx = 1 2 B ( 7 2 , 5 2 )
= 1 2 Γ ( 7 2 ) . Γ ( 5 2 ) Γ ( 6 ) = 1 2 . 45 32 . Γ ( 1 2 ) . Γ ( 1 2 ) 5 ! = 3 π 512
Quảng cáo
Câu 3 : Biết ∫ 0 + ∞ x 6 3 - x 4 dx = a π b ( ln 3 ) 7 / 2
A. a - b = -1
B. a + b = 10
C. a > b
D. a.b < 100
Hiển thị đáp án
Chọn đáp án A
Giải thích:
Đặt ln 3.x2 = u
⇒ ∫ 0 π 2 x 6 . 3 - x 2 dx = ∫ 0 π 2 u 3 ( ln 3 ) 3 e - u 2 ln 3 . u du = 1 2 ∫ 0 π 2 ( ln 3 ) - 7 2 . u 5 2 e - u du
= ( ln 3 ) - 7 2 2 ∫ 0 π 2 u 7 2 - 1 . e - u du = ( ln 3 ) - 7 2 2 . Γ ( 7 2 ) = 15 π 16 ( ln 3 ) 7 2
⇒
Câu 4 : Biểu diễn tích phân ∫ 0 + ∞ x 2 ( 1 + x 4 ) 4 dx
A. Γ ( 3 4 ) Γ ( 13 4 ) 6 Γ ( 4 )
B. Γ ( 3 4 ) Γ ( 1 4 ) 4 Γ ( 4 )
C. Γ ( 3 4 ) Γ ( 13 4 ) 4 Γ ( 4 )
D. Γ ( 3 4 ) Γ ( 5 4 ) 4 Γ ( 4 )
Hiển thị đáp án
Chọn đáp án C
Giải thích:
Đặt x4 = u
⇒ ∫ 0 + ∞ x 2 ( 1 + x 4 ) 4 dx = 1 4 ∫ 0 + ∞ u - 1 4 d u ( 1 + u ) 4 = 1 4 B ( 3 4 , 13 4 ) = 1 4 Γ ( 3 4 ) . Γ ( 13 4 ) Γ ( 4 )
Câu 5 : Tính tích phân ∫ 0 1 1 1 - x 30 30 dx
Quảng cáo
A. π 30 sin ( π 20 )
B. π 30 sin ( π 30 )
C. π sin ( π 30 )
D. π 50 sin ( π 30 )
Hiển thị đáp án
Chọn đáp án B
Giải thích:
Đặt u = x30
⇒ ∫ 0 1 1 1 - x 30 30 dx = 1 30 ∫ 0 1 u 29 20 1 - u 30 du = 1 30 ∫ 0 1 u 1 30 - 1 . ( 1 - u ) 29 30 - 1 du = 1 30 B ( 1 30 , 29 30 ) = 1 30 π sin ( π 30 )
Câu 6 : Tính tích phân ∫ 0 + ∞ x 4 ( x 3 + 1 ) 2 dx
A. 4 3 π 27
B. 4 2 π 27
C. 2 2 π 27
D. 2 3 π 27
Câu 7 : Tính tích phân ∫ 0 1 ( ln 1 x ) 10 dx
A. 11!
B. 10!
C. 12!
D. 9!
Hiển thị đáp án
Chọn đáp án B
Giải thích:
Đặt ln (1 x
⇒ ∫ 0 1 ( ln 1 x ) 10 dx = - ∫ + ∞ 0 u 10 . e - u du = ∫ 0 + ∞ u 11 - 1 . e - u du = Γ ( 11 )
Quảng cáo
Câu 8 : Tính tích phân ∫ 0 1 x 5 ( ln x ) 10 dx
A. 10 ! 5 11
B. 10 ! 6 11
C. 11 ! 5 11
D. 11 ! 6 11
Hiển thị đáp án
Chọn đáp án B
Giải thích:
Đặt ln x = u
⇒ ∫ 0 1 x 5 ( ln x ) 10 dx = ∫ - ∞ 0 e 6 u . u 10 du
Đặt 6u = -t ⇒ - d t 6 u 10 = t 10 6 10
Đổi cận: u = 0 ⇒ → ⇒ →
⇒ ∫ - ∞ 0 e 6 u . u 10 du = 1 6 11 ∫ 0 + ∞ e - t . t 10 dt = 1 6 11 Γ ( 11 ) = 10 ! 6 11
Câu 9 : Biểu diễn tích phân ∫ - ∞ 0 e 2 x 1 - e 3 x 3 dx
A. Γ ( 2 3 ) Γ ( 4 3 ) 2 . Γ ( 2 )
B. Γ ( 2 3 ) Γ ( 1 3 ) 3 . Γ ( 2 )
C. Γ ( 2 3 ) Γ ( 1 3 ) 9 . Γ ( 2 )
D. Γ ( 2 3 ) Γ ( 4 3 ) 3 . Γ ( 2 )
Hiển thị đáp án
Chọn đáp án C và D
Giải thích:
Đặt I = ∫ - ∞ 0 e 2 x 1 - e 3 x 3 dx
Đặt u = e3x ⇒ 3x dx ⇒ d u 3 e 3 x = u - 1 d u 3
Với x = 0 ⇒ ⇒
I = 1 3 ∫ 0 1 u 2 3 ( 1 - u ) 1 3 u - 1 du = 1 3 ∫ 0 1 u - 1 3 ( 1 - u ) 1 3 du = 1 3 B ( 2 3 , 4 3 ) = 1 3 Γ ( 2 3 ) . Γ ( 4 3 ) Γ ( 2 )
Mà Γ ( 4 3 ) = 1 3 Γ ( 1 3 ) ⇒ I = 1 9 Γ ( 2 3 ) . Γ ( 1 3 ) 1 ! = 1 9 2 3 π 1 ! = 2 9 3 π
Câu 10 : Tính tích phân ∫ 0 π 2 sin 7 x c o s 5 x dx
A. 5 π 128 2
B. 3 π 256 2
C. π 256 2
D. 7 π 256 2
Hiển thị đáp án
Chọn đáp án A
Giải thích:
∫ 0 π 2 ( sin x ) 7 2 ( c o s x ) 5 2 dx = ∫ 0 π 2 ( sin x ) 2 . 9 4 - 1 ( c o s x ) 2 . 7 4 - 1 dx = 1 2 B ( 9 4 , 7 4 ) = 1 2 Γ ( 9 4 ) . Γ ( 7 4 ) Γ ( 4 )
⇒ T P = 1 2 . B ( 9 4 , 7 4 ) = 1 2 . 15 16 . Γ ( 1 4 ) . Γ ( 3 4 ) Γ ( 4 ) = 15 128 2 2 π 3 ! = 5 π 128 2
II. Bài tập trắc nghiệm Tích phân đường
1. Tích phân đường loại I:
Câu 11 : Tính tích phân ∫ L ( x + y ) ds
A. 35 2
B. 35 4
C. 35 3
D.35 6
Hiển thị đáp án
Chọn đáp án A
Giải thích:
Phương trình đoạn OA là
⇒ ∫ L ( x + y ) ds = ∫ 0 4 ( x + 3 4 x ) 5 4 dx = 35 2
Câu 12 : Tính ∫ L ( x + y ) ds
A. 4 + 8π
B. 8 + 4π
C. 4π
D. 2 + 4π
Hiển thị đáp án
Chọn đáp án B
Giải thích:
Đường C:
⇒ d s = x ' 2 ( t ) + y ' 2 ( t ) d t
⇒ ∫ L ( x + y ) ds = 2 ∫ 0 π ( 2 + 2 c o s t + 2 sin t ) dt π
Câu 13 : Tìm m để ∫ C ( m x - y ) ds y = 9 - x 2
A. m = 1
B. m = 2
C. m = 3
D. m = 4
Hiển thị đáp án
Chọn đáp án C
Giải thích:
Nửa đường tròn C:
Đặt
⇒ ∫ C ( m x - y ) ds = 3 ∫ 0 π ( 3 m c o s t - 3 sin t ) dt ⇒
Câu 14 : Với C là đường tròn x2 + y2 = 2x, tính ∫ C ( x - y ) ds
A. π
B. 2π
C. 3π
D. 6π
Hiển thị đáp án
Chọn đáp án B
Giải thích:
C: x2 + y2 = 2x ⇔ 2 + y2 = 1
Đặt
⇒ ∫ C ( x - y ) ds = ∫ 0 2 x ( 1 + c o s t - sin t ) dt = 2 π
Câu 15 : Tính ∫ C ( x + y ) ds 2 = cos 2φ π 4 φ π 4
A. 5
B. 6
C. 10
D. 2
Hiển thị đáp án
Chọn đáp án D
Giải thích:
Cung C:
⇒ d s = r 2 ( φ ) + r ' 2 ( φ ) d φ = c o s 2 φ + sin 2 2 φ c o s 2 φ d φ = 1 c o s 2 φ d φ
Đặt
⇒ ∫ - π 4 π 4 r ( c o s φ + sin φ ) 1 c o s 2 φ d φ = ∫ - π 4 π 4 c o s 2 φ ( c o s φ + sin φ ) 1 c o s 2 φ d φ = 2
Câu 16 : Với C là đường cong x2/3 + y2/3 = 1 trong góc phần tư thứ nhất nối A (1, 0) và B (0, 1), tính ∫ C ( y 2 + 1 ) ds
A. 15 8
B. 15 9
C. 15 7
D. 15 4
Hiển thị đáp án
Chọn đáp án A
Giải thích:
Ta có C: x2/3 + y2/3 = 1 ⇔ 1/3 )2 + (y1/3 )2 = 1
Tham số hóa:
⇒ d s = x ' 2 ( t ) + y ' 2 ( t ) d t = 9 sin 2 t c o s 4 t + 9 c o s 2 t sin 4 t d t
Tại
⇒ ∫ C ( y 2 + 1 ) ds = 3 ∫ 0 π 2 ( sin 6 t + 1 ) sin t c o s t dt = 3 ∫ 0 π 2 ( sin 7 t + sin t ) d ( sin t ) = 3 ∫ 0 1 ( u 7 + u ) du = 15 8
Câu 17 : Tính ∫ C y ds 2 đi từ O (0, 0) đến A (1, 1)
A. 1 3 ( 5 5 - 1 )
B. 1 12 ( 5 5 - 1 )
C. 1 6 ( 5 5 - 1 )
D. 1 2 ( 5 5 - 1 )
Hiển thị đáp án
Chọn đáp án B
Giải thích:
Đường C: ⇒ ⇒ 1 + x ' 2 ( y ) d y = 1 + 4 y 2 d y
⇒ ∫ C y ds = ∫ 0 1 y 1 + 4 y 2 d y = 1 2 ∫ 0 1 1 + 4 y 2 d ( y 2 ) = 1 2 ∫ 0 1 1 + 4 u du = 1 12 ( 5 5 - 1 )
Câu 18 : Tính ∫ L x y ds
A. 20
B. 25
C. 24
D. 18
Hiển thị đáp án
Chọn đáp án C
Giải thích:
Ta có: ∫ L x y ds = ∫ A B x y ds + ∫ B C x y ds + ∫ C D x y ds + ∫ D A x y ds
Phương trình AB:
Phương trình BC:
Phương trình CD:
Phương trình DA:
Câu 19 : Tính ∮ C x y d s
A. 1
B. 4
C. 2
D. 0
Hiển thị đáp án
Chọn đáp án D
Giải thích:
Đường C: |x| + |y| = 1
Phương trình AB:
Phương trình BC:
Phương trình CD:
Phương trình DA:
∮ C x y d s = ∫ A B x y ds + ∫ B C x y ds + ∫ C D x y ds + ∫ D A x y ds
Xét ∫ A B x y ds d s = 1 + y ' 2 ( x ) d x = 2 d x ⇒ ∫ A B x y ds = 2 ∫ 0 1 x ( 1 - x ) dx = 2 6
Xét ∫ B C x y ds d s = 1 + y ' 2 ( x ) d x = 2 d x ⇒ ∫ B C x y ds = 2 ∫ 0 1 x ( x - 1 ) dx = - 2 6
Xét ∫ C D x y ds d s = 1 + y ' 2 ( x ) d x = 2 d x
⇒ ∫ C D x y ds = 2 ∫ - 1 0 x ( - x - 1 ) dx = - 2 6
Xét ∫ D A x y ds d s = 1 + y ' 2 ( x ) d x = 2 d x ⇒ ∫ D A x y ds = 2 ∫ - 1 0 x ( x + 1 ) dx = - 2 6
⇒ ∮ C x y d s = ∫ A B x y ds + ∫ B C x y ds + ∫ C D x y ds + ∫ D A x y ds
Câu 20 : Tính ∫ L x 2 + y 2 ds 2 + y2 = 2x
A. 8
B. 6
C. 4
D. 10
Hiển thị đáp án
Chọn đáp án A
Giải thích:
Đặt ⇒
⇒ d s = r 2 ( φ ) + r ' 2 ( φ ) d φ = 4 c o s 2 φ + 4 sin 2 φ d φ = 2 φ
∫ L x 2 + y 2 ds = ∫ - π 2 π 2 r 2 . 2 dφ = 2 ∫ - π 2 π 2 r dφ = 2 ∫ - π 2 π 2 2 c o s φ dφ = 8
2. Tích phân đường loại II:
Câu 21 : Tính ∫ A B ( x - 3 y ) dx + 2 y d y A B ⏜ 2 , A (1,0), B (-1, 0)
A. 0
B. 2
C. 4
D. 6
Hiển thị đáp án
Chọn đáp án C
Giải thích:
Cung A B ⏜
⇒ ∫ A B ⏜ ( x - 3 y ) dx + 2 y d y = ∫ 1 - 1 [ x - 3 ( 1 - x 2 ) ] dx + ∫ 1 - 1 2 ( 1 - x 2 ) . ( - 2 x ) dx = 4
Câu 22 : Tính ∫ A B C 5 y 4 dx - 4 x 3 d y
A. 2
B. 3
C. 5
D. 4
Hiển thị đáp án
Chọn đáp án C
Giải thích:
∫ A B C 5 y 4 dx - 4 x 3 d y = ∫ A B 5 y 4 dx - 4 x 3 d y + ∫ B C 5 y 4 dx - 4 x 3 d y 1 + I2
Đoạn thẳng AB:
⇒ I 1 = ∫ 0 1 5 ( 1 - x ) 4 dx + ∫ 0 1 ( - 4 x 3 ) . ( - dx ) = 2
Đoạn thẳng BC:
⇒ I 2 = ∫ 1 0 5 ( x - 1 ) 4 dx + ∫ 1 0 ( - 4 x 3 ) . dx = 0
∫ A B C 5 y 4 dx - 4 x 3 d y 1 + I2 = 2
Câu 23 : Tìm m để ∫ C ( x + x y ) dx + m x 2 d y = - 10 3 2 + y2 = 4 đi từ A (-2, 0) đến B (0, 2)
A. 2
B. 3/2
C. 0
D. 1/3
Hiển thị đáp án
Chọn đáp án D
Giải thích:
Đặt π π I = ∫ C ( x + x y ) dx + m x 2 d y
I = ∫ π π 2 [ ( 2 c o s t + 4 c o s t ) ( - 2 sin t ) + m . ( 2 c o s t ) 2 ( 2 c o s t ) ] dt
= ∫ π π 2 ( - 4 c o s t sin t - 8 c o s t sin 2 t + 8 m c o s 3 t ) dt
= ∫ π π 2 ( - 4 sin t - 8 sin 2 t + 8 m c o s 2 t ) c o s t dt
= ∫ π π 2 ( - 4 sin t - 8 sin 2 t + 8 m - 8 m sin 2 t ) c o s t dt
= ∫ π π 2 [ - 4 sin t - ( 8 + 8 m ) sin 2 t + 8 m ] d ( sin t )
= ∫ 0 1 [ - 4 u - ( 8 + 8 m ) u 2 + 8 m ] d ( u ) = - 10 3
⇒
Câu 24 : Tính ∮ L ( x y + e x sin x + x + y ) d x + ( - x y + e - y - x + sin y ) d y 2 + y2 = 2x theo chiều dương.
A. -3π
B. 3π
C. -2π
D. 4π
Hiển thị đáp án
Chọn đáp án A
Giải thích:
Đặt I = ∮ L ( x y + e x sin x + x + y ) d x + ( - x y + e - y - x + sin y ) d y
Đặt: P = xy + ex sin x + x + y, Q = -xy + e-y - x + sin y
⇒ y = x + 1, Q'x = -y - 1. P'y , Q'x liên tục với x, y ∈ R.
Đường cong L kín hướng dương, giới hạn miền D: x2 + y2 ≤ 2x
Áp dụng công thức Green, ta có:
I = ∬ D ( - y - x - 2 ) d x d y
Nhận xét: hàm số f (x, y) = -y là hàm lẻ với biến y, miền D đối xứng qua trục Ox
⇒ ∬ D - y d x d y I = ∬ D ( - x - 2 ) d x d y
Đặt:
I = ∫ 0 2 π dφ ∫ 0 1 ( - r c o s φ - 3 ) r d r = ∫ 0 2 π ( - 1 3 c o s φ - 3 2 ) dφ = - 3 π
Câu 25 : Tính ∮ L 2 x d x - [ x 2 + 2 y + e y 2 + 1 + sin ( y 2 ) ] d y
A. 1
B. 2
C. 4
D. 6
Hiển thị đáp án
Chọn đáp án B
Giải thích:
Đặt I = ∮ L 2 x d x - [ x 2 + 2 y + e y 2 + 1 + sin ( y 2 ) ] d y
Đặt
y , Q'x liên tục với x, y ∈ R
Gọi D là miền được giới hạn bởi chu tuyến ∆
D được giới hạn bởi các đường:
L là đường cong kín, hướng âm, giới hạn miền D. Áp dụng công thức Green:
I = - ∬ D - 2 x d x d y = ∬ D 2 x d x d y = ∫ 0 2 d y ∫ y - 2 2 2 - y 2 x dx
................................
................................
................................
Xem thêm câu hỏi trắc nghiệm các môn học Đại học có đáp án hay khác:
Sách VietJack thi THPT quốc gia 2025 cho học sinh 2k7:
ĐỀ THI, GIÁO ÁN, GÓI THI ONLINE DÀNH CHO GIÁO VIÊN VÀ PHỤ HUYNH LỚP 12
Bộ giáo án, đề thi, bài giảng powerpoint, khóa học dành cho các thầy cô và học sinh lớp 12, đẩy đủ các bộ sách cánh diều, kết nối tri thức, chân trời sáng tạo tại https://tailieugiaovien.com.vn/ VietJack Official
Giải bài tập lớp 12 Kết nối tri thức khác











 Tham số hóa C
Tham số hóa C





 x' (y) = 2y ds =
x' (y) = 2y ds = 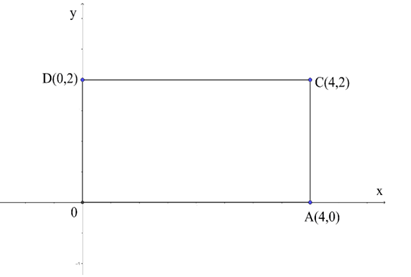










 Đường cong L:
Đường cong L: 




 với t chạy từ đến /2. Đặt
với t chạy từ đến /2. Đặt 
 |J| = r. Miền (D):
|J| = r. Miền (D): 


 , P'y, Q'x liên tục với x, y ∈ R
, P'y, Q'x liên tục với x, y ∈ R





 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp



