Đề thi Học kì 2 Toán 8 năm 2023-2024 trường THCS Đa Tốn (Hà Nội)

Với đề thi Học kì 2 Toán 8 năm 2023-2024 trường THCS Đa Tốn, Hà Nội có đáp án sẽ giúp bạn ôn tập và đạt điểm cao trong bài thi Toán 8.

Đề thi Học kì 2 Toán 8 năm 2023-2024 trường THCS Đa Tốn (Hà Nội)

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 1 trường THCS Đa Tốn (Hà Nội)

Năm học 2023-2024

Môn: Toán 8

Thời gian làm bài: phút

(Đề 1)

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm):

Chọn chữ cái đứng trước câu trả lời đúng nhất cho mỗi câu hỏi sau và ghi vào giấy làm bài.

Câu 1. Với điều kiện nào của x thì phân thức $\frac{{\left(x-1\right)}^3}{\left(x-2\right)\left(x+3\right)}$ có nghĩa?

A. $x\le 2$

B. $x\ne 2;x\ne -3$

C. $x\ne -3$

D. $x\ne 2$

Câu 2. Kết quả của tích $\frac{10x^3}{11y^2}\cdot \frac{121y^5}{25x}$ là:

A. $\frac{11x^2{y}^3}{5}$

B. $\frac{22x^2{y}^3}{5}$

C. $\frac{22x^2{y}^3}{25}$

D. $\frac{22x^3{y}^3}{5}$

Câu 3. Phương trình nào sau đây là phương trình bậc nhất một ẩn?

A. 0x - 5 = 0

B. $2x^2-4=0$

C. 2x - 3 = 0

D. $\frac{5}{x}+1=0.$

Câu 4.    Đồ thị hàm số y = x + 2 đi qua điểm nào sau đây?

A. A(0; 2)

B. B(2; 0)

C. C(-1; 3)

D. D(-2; 4)

Câu 5. Nghiệm của phượng trình 3x - 9 = 0 là :

A. x = 3

B. x = - 3

C. $x=\frac{1}{3}$

D. $x=\frac{-1}{3}$

Câu 6. Xác định đường thẳng $y=ax+b\left(a\ne 0\right)$ có hệ số góc bằng 2 và đi qua điểm A(2; 1) :

A. y = -2x + 3

B. y = 2x + 5

C. y = - 2x - 3

D. y = 2x - 3

Câu 7. Tìm tất cả giá trị của m để đường thẳng y = mx + 2 cắt đường thẳng y = 2x + 3 .

A. $m=\pm 2.$

B. $m\ne \pm 2.$

C. $m\ne 2.$

D. $m\ne -2.$

Câu 8. Nếu $\Delta ABC\backsim \Delta MNP$ theo tỉ số $k=\frac{2}{3}$ thì $\Delta MNP\backsim \Delta ABC$ theo tỉ số:

A. $\frac{2}{3}$

B. $\frac{3}{2}$

C. $\frac{4}{9}$

D. $\frac{4}{3}$

Câu 9. Cho $\Delta DEF\backsim \Delta HKI$. Tỉ số nào sau đây là đúng?

A. $\frac{DE}{HK}=\frac{DF}{KI}$

B. $\frac{DE}{HK}=\frac{EF}{HI}$

C. $\frac{EF}{KI}=\frac{DF}{HI}$

D. $\frac{DF}{HI}=\frac{EF}{HK}$

Câu 10. Trong các phát biểu sau, phát biểu nào là định lý Pythagore?

        A. Trong một tam giác vuông, bình phương một cạnh bằng tổng  bình phương của hai cạnh còn lại.

        B. Nếu một tam giác có  một cạnh bằng tổng của hai cạnh  còn lại thì tam giác đó là tam giác vuông.

        C. Nếu một tam giác có bình phương cạnh huyền bằng hiệu bình phương của hai cạnh góc vuông thì tam giác đó là tam giác vuông.

        D. Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.

Câu 11. Cho hình chóp tam giác đều S.MNP , đỉnh của hình chóp là:

A. S

B. M

C. N

D. P

Câu 12. Số mặt bên của hình chóp tam giác đều S.ABC là:

A. 4.

B. 2. 

C. 1.

D. 3.

PHẦN II. TỰ LUẬN (7,0 điểm)

Bài 1. (1,5 điểm) Giải các phương trình sau:

a) 5x - 7 = 2x + 5

b) $3(x-2)+x^2=x(x-4)$

c) $\frac{3x-1}{2}+\frac{x}{3}=\frac{2x+1}{6}$

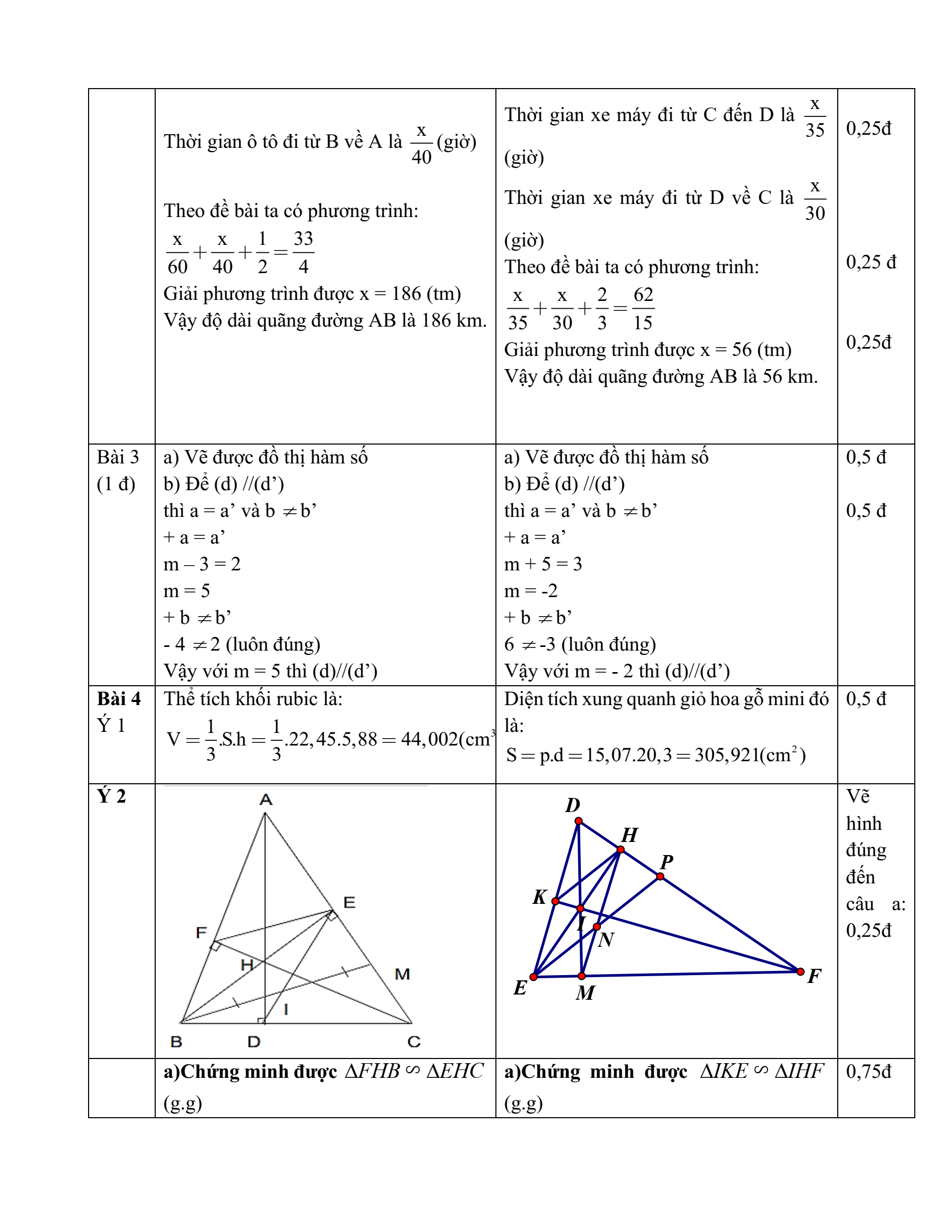
Bài 2. (1,0 điểm) Một người đi ô tô từ A đến B với vận tốc 60km/h. Sau khi đến B và nghỉ lại ở đó 30 phút, ô tô lại đi từ B về A với vận tốc 40km/h. Tổng thời gian cả đi lẫn về là

8 giờ 15 phút (bao gồm cả thời gian nghỉ). Tính quãng đường AB.

Bài 3. (1,0 điểm) Cho hàm số bậc nhất y = 2x - 4  có đồ thị là đường thẳng (d).

a) Vẽ đồ thị hàm số trên.

b) Tìm m để đường thẳng (d'): y = (m - 3)x + 2 song song với đường thẳng (d).

Bài 4. (3,0 điểm)

1. Một khối rubik có dạng hình chóp tam giác đều với diện tích đáy là $22,45{\text{\hspace{0.17em}\hspace{0.17em}cm}}^{\text{2}}$và chiều cao là 5,88 cm.Tính thể tích của khối rubik đó.

2. Cho tam giác ABC nhọn (AB < AC) có hai đường cao BE, CF cắt nhau tại H

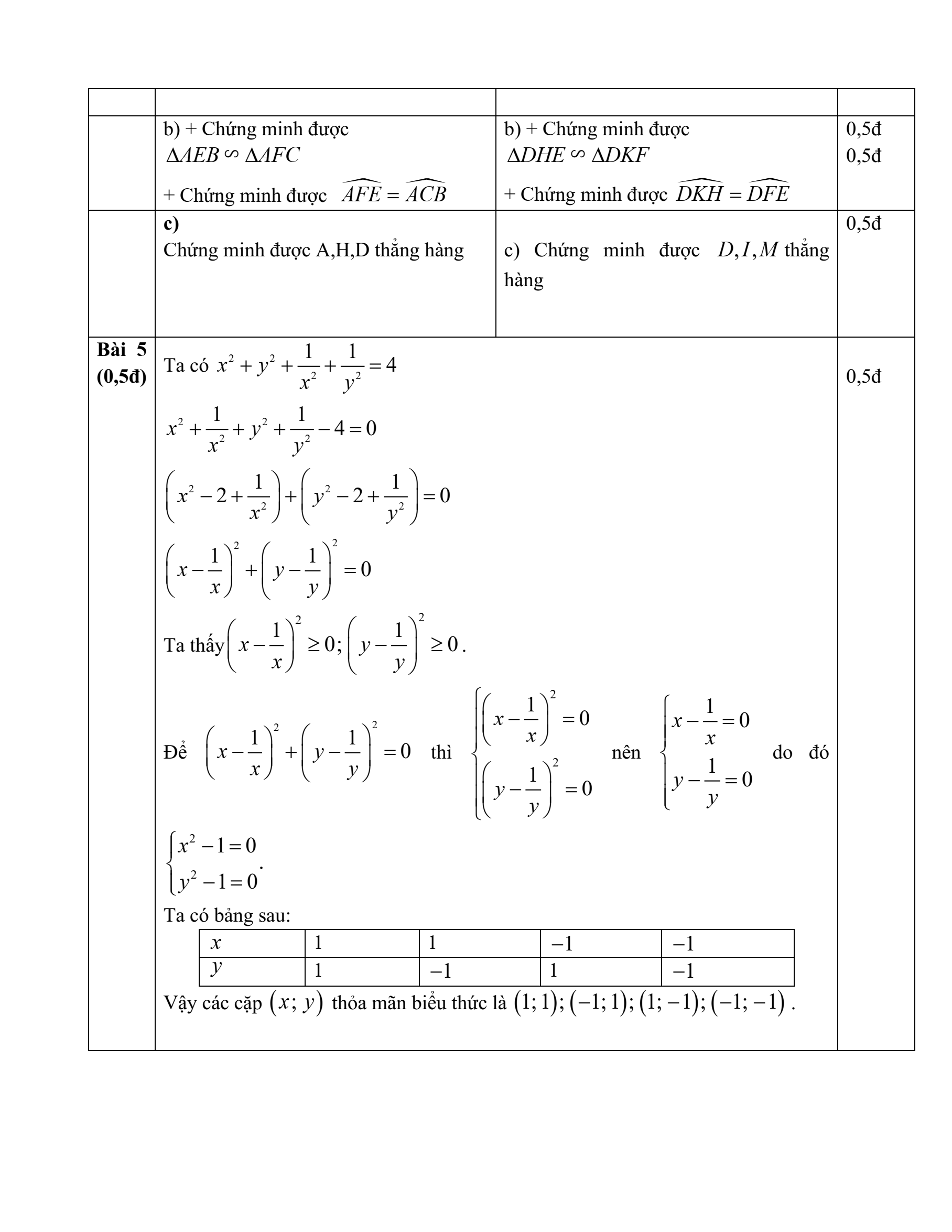
a) Chứng minh: $\Delta FHB\backsim \Delta EHC$.

b) Chứng minh: $\Delta AEB\backsim \Delta AFC$ và $\widehat{AFE}=\widehat{ACB}$.

c) Đường thẳng qua B và song song với EF cắt AC tại M Gọi I là trung điểm của BM,D là giao điểm của EI và BC Chứng minh ba điểm A, H, D thẳng hàng.

Bài 5 (0,5 điểm) Tìm x, y  biết rằng $x^2+y^2+\frac{1}{x^2}+\frac{1}{y^2}=4.$

Phòng Giáo dục và Đào tạo .....

Đề thi Học kì 1 trường THCS Đa Tốn (Hà Nội)

Năm học 2023-2024

Môn: Toán 8

Thời gian làm bài: phút

(Đề 2)

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm):

Chọn chữ cái đứng trước câu trả lời đúng nhất cho mỗi câu hỏi sau và ghi vào giấy làm bài.

Câu 1. Với điều kiện nào của x thì phân thức $\frac{{\left(x-2\right)}^2}{\left(x+5\right)\left(x-1\right)}$ có nghĩa?

A. $x\ne -5;x\ne 1$

B. $x\ge 1$

C. $x\ne -5$

D. $x\ne 1$

Câu 2. Kết quả của tích $\frac{15x^4}{9y^3}\cdot \frac{81y^5}{12x^2}$ là:

A. $\frac{45x^2{y}^3}{4}$

B. $\frac{45x^2{y}^2}{4}$

C. $\frac{108x^2{y}^3}{16}$

D. $\frac{25x^3{y}^3}{7}$

Câu 3. Hàm số nào sau đây là hàm số bậc nhất?

A. $y=0.x+3$

B. $y=x^2-4$

C. $y=\frac{5}{x}-2$

D. $y=2x+7$

Câu 4. Đồ thị hàm số y = x - 2 đi qua điểm nào sau đây?

A. A90; 2)

B. B(2; 0)

C. C(-1; 3)

D. D(-2; 4)

Câu 5. Nghiệm của phượng trình 4x - 16 = 0 là :

A. x = - 4

B. $x=\frac{1}{4};$

C. x = 4

D. $x=\frac{-1}{4}$

Câu 6. Xác định đường thẳng $y=ax+b\left(a\ne 0\right)$ có hệ số góc bằng 3 và đi qua điểm B(1; 2) :

A. y = -3x -1

B. y = 3x + 1

C. y = 3x - 1

D. y = - 3x +1

Câu 7. Tìm tất cả giá trị của m để đường thẳng y = mx - 5 cắt đường thẳng y = -2x + 8 .

A. $m=\pm 2.$

B. $m\ne \pm 2.$

C. $m\ne 2.$

D. $m\ne -2.$

Câu 8. Nếu $\Delta DEF\backsim \Delta HPQ$ theo tỉ số $k=\frac{4}{5}$ thì $\Delta HPQ\backsim \Delta DEF$ theo tỉ số:

A. $\frac{5}{4}$

B. $\frac{4}{5}$

C. $\frac{16}{25}$

D. $\frac{25}{16}$

Câu 9. Cho $\Delta MNP\backsim \Delta ADC$.  Tỉ số nào sau đây là đúng?

A. $\frac{MN}{AD}=\frac{NP}{DC}$

B. $\frac{MN}{AD}=\frac{MP}{DC}$

C. $\frac{MN}{DC}=\frac{NP}{AC}$

D. $\frac{MP}{AC}=\frac{MN}{DC}$

Câu 10. Trong các phát biểu sau, phát biểu nào là định lý Pythagore đảo?

        A. Trong một tam giác vuông, bình phương một cạnh bằng tổng  bình phương của hai cạnh còn lại.

        B. Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.

        C. Nếu một tam giác có bình phương cạnh huyền bằng hiệu bình phương của hai cạnh góc vuông thì tam giác đó là tam giác vuông.

        D. Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương của hai cạnh góc vuông.

Câu 11. Cho hình chóp tam giác đều S.ABC, mặt đáy của hình chóp là:

A. $\Delta SAB$

B. $\Delta ASC$

C. $\Delta ABC$

D. $\Delta SBC$

Câu 12. Số cạnh bên của hình chóp tam giác đều S.ABC  là:

A. 4.

B. 2. 

C. 1.

D. 3.

PHẦN II. TỰ LUẬN (7,0 điểm)

Bài 1. (1,5 điểm) Giải các phương trình sau:

a) 7x - 3 = 4x + 6

b) $2(x-4)+x^2=x(x-5)$

c) $\frac{2x+3}{5}+\frac{x}{2}=\frac{3x-5}{10}$

Bài 2. (1,0 điểm) Một người đi máy từ C đến D với vận tốc 35 km/h. Khi đến D người đó nghỉ 40 phút rồi quay trở lại C với vận tốc 30 km/h. Tính độ dài quãng đường CD biết thời gian cả đi lẫn về ( tính cả thời gian nghỉ) là 4 giờ 8 phút.

Bài 3. (1,0 điểm) Cho hàm số bậc nhất y = 3x + 6 có đồ thị là đường thẳng (d).

a) Vẽ đồ thị hàm số trên.

b) Tìm m để đường thẳng (d'): y = (m + 5)x - 3  song song với đường thẳng (d).

Bài 4. (3,0 điểm)

1. Một giỏ hoa gỗ mini có dạng hình chóp tam giác đều (như hình bên) có nửa chu vi đáy là 15,07 cm và độ dài trung đoạn bằng 20,3 cm. Tính diện tích xung quanh giỏ hoa gỗ mini đó.

2. Cho tam giác DEF nhọn (DE < DF) có hai đường cao EH, FK cắt nhau tại I

a) Chứng minh: $\Delta IKE\backsim \Delta IHF$.

b) Chứng minh: $\Delta DHE\backsim \Delta DKF$ và $\widehat{DKH}=\widehat{DFE}$.

c) Đường thẳng qua E và song song với HK cắt DF tại P Gọi N là trung điểm của EP, M là giao điểm của HN và EF Chứng minh ba điểm D, I, M thẳng hàng.

Bài 5 (0,5 điểm) Tìm x, y  biết rằng $x^2+y^2+\frac{1}{x^2}+\frac{1}{y^2}=4.$

Đáp án Đề thi Học kì 2 trường THCS Đa Tốn (Hà Nội)

Xem thêm đề thi Học kì 2 Toán 8 năm 2023-2024 Hà Nội hay khác:

• Đề thi Học kì 2 Toán 8 năm 2023-2024 trường THCS Lê Quý Đôn (Hà Nội)

• Đề thi Học kì 2 Toán 8 năm 2023-2024 trường THCS Đống Đa (Hà Nội)

• Đề thi Học kì 2 Toán 8 năm 2023-2024 phòng GD&ĐT Đan Phượng (Hà Nội)

• Đề thi Học kì 2 Toán 8 năm 2023-2024 trường THCS Phúc Đồng (Hà Nội)

• Đề thi Học kì 2 Toán 8 năm 2023-2024 trường THCS Ngọc Lâm (Hà Nội)

• Đề thi Học kì 2 Toán 8 năm 2023-2024 phòng GD&ĐT Hai Bà Trưng (Hà Nội)

• Đề thi Học kì 2 Toán 8 năm 2023-2024 phòng GD&ĐT Thanh Trì (Hà Nội)

• Đề thi Học kì 2 Toán 8 năm 2023-2024 trường THCS Văn Quán (Hà Nội)

• Đề thi Học kì 2 Toán 8 năm 2023-2024 trường THCS Chương Dương (Hà Nội)

• Đề thi Học kì 2 Toán 8 năm 2023-2024 trường THCS Giảng Võ (Hà Nội)

---