Tổng hợp lý thuyết Toán 8 Chương 5 Chân trời sáng tạo

Tổng hợp lý thuyết Toán 8 Chương 5: Hàm số và đồ thị sách Chân trời sáng tạo hay nhất, chi tiết cùng các bài tập có lời giải sẽ giúp học sinh lớp 8 nắm vững kiến thức trọng tâm Toán 8 Chương 5.

Tổng hợp lý thuyết Toán 8 Chương 5 Chân trời sáng tạo

(199k) Xem Khóa học Toán 8 CTST

Lý thuyết tổng hợp Toán 8 Chương 5

1. Khái niệm hàm số

Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của biến số x.

2. Giá trị của hàm số

Cho hàm số y = f(x), nếu ứng với x = a ta có y = f(a) thì f(a) được gọi là giá trị của hàm số y = f(x) tại x = a.

3. Tọa độ của một điểm

3.1. Mặt phẳng tọa độ

Trên mặt phẳng, ta vẽ hai trục số Ox, Oy vuông góc với nhau và cắt nhau tại gốc O của mỗi trục, khi đó ta có hệ trục tọa độ Oxy.

Các trục Ox, Oy gọi là các trục tọa độ. Ox gọi là trục hoành và thường được vẽ nằm ngang, Oy gọi là trục tung và thường được vẽ thẳng đứng. Giao điểm O được gọi là gốc tọa độ.

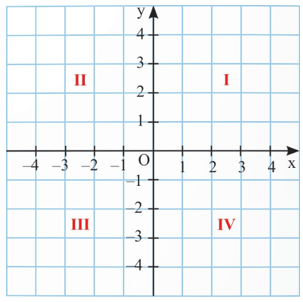
Mặt phẳng có hệ trục tọa độ Oxy gọi là mặt phẳng tọa độ Oxy. Hai trục Ox, Oy chia mặt phẳng tọa độ Oxy thành bốn gốc: góc phần tư thứ I, II, III, IV.

Các đơn vị dài trên hai trục tọa độ thường được chọn bằng nhau (nếu không nói gì thêm).

3.2. Tọa độ của một điểm trong mặt phẳng tọa độ

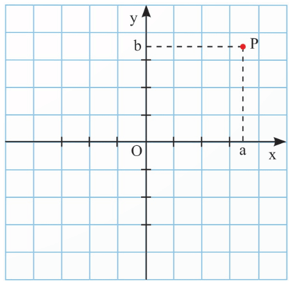
Ta xác định vị trí một điểm P trong mặt phẳng tọa độ Oxy bằng cách dùng hai trục số thực như sau:

Từ P vẽ các đường vuông góc với các trục tọa độ cắt trục hoành tại điểm a và trục tung tại điểm b gọi là tọa độ của điểm P và kí hiệu P(a; b). Số a gọi là hoành độ và số b gọi là tung độ của điểm P.

Gốc tọa độ O có tọa độ (0; 0).

Chú ý: Trên mặt phẳng tọa độ, mỗi điểm P xác định đúng một cặp số (a; b).

4. Xác định một điểm trên mặt phẳng tọa độ khi biết tọa độ của chính nó

Để xác định một điểm P có tọa độ là (a; b), ta thực hiện các bước sau:

− Tìm trên trục hoành điểm a và vẽ đường thẳng vuông góc với trục này tại điểm a.

− Tìm trên trục tung điểm b và vẽ đường thẳng vuông góc với trục này tại điểm b.

− Giao điểm của hai đường thẳng vừa vẽ cho ta điểm P cần tìm.

Chú ý: Trên mặt phẳng tọa độ, mỗi cặp số (a; b) xác định một điểm P duy nhất.

5. Đồ thị của hàm số

Đồ thị của hàm số y = f(x) trên mặt phẳng tọa độ Oxy là tập hợp tất cả các điểm M(x; f(x)).

6. Hàm số bậc nhất

Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b với a, b là các số cho trước và a ≠ 0.

7. Đồ thị của hàm số bậc nhất

7.1. Đồ thị hàm số y = ax (a ≠ 0)

Đồ thị của hàm số y = ax (a ≠ 0) là một đường thẳng đi qua gốc tọa độ O(0; 0).

Cách vẽ:

Để vẽ đồ thị của hàm số y = ax (a ≠ 0), ta thường thực hiện các bước sau:

Bước 1: Xác định một điểm M trên đồ thị khác gốc tọa độ, chẳng hạn M(1; a).

Bước 2: Vẽ đường thẳng đi qua hai điểm O vàM.

Chú ý: Đồ thị hàm số y = ax còn được gọi là đường thẳng y = ax.

7.2. Đồ thị hàm số y = ax + b (a ≠ 0; b≠ 0)

Đồ thị của hàm số y = ax + b (a ≠ 0, b ≠ 0) là một đường thẳng:

− Cắt trục tung tại điểm có tung độ bằng b;

− Song song với đường thẳng y = ax.

Cách vẽ:

Để vẽ đồ thị của hàm số y = ax + b (a ≠ 0; b ≠ 0), ta chỉ cần xác định được hai điểm phân biệt tùy ý thuộc đồ thị rồi vẽ đường thẳng đi qua hai điểm đó. Thông thường ta xác định hai điểm đặc biệt là giao điểm của đồ thị với hai trục tọa độ.

Bước 1: Cho x = 0 thì y = b, ta được điểm M(0; b) trên Oy.

Cho y = 0 thì $x=\frac{-b}{a}$ , ta được điểm N$(\frac{-b}{a};0)$trên Ox.

Bước 2: Vẽ đường thẳng đi qua hai điểm M và N, ta được đồ thị của hàm số y = ax + b.

Chú ý:Đồ thị của hàm số y = ax + b còn gọi là đường thẳng y = ax + b.

8. Hệ số góc của đường thẳng

• Ta nhận thấy

− Khi hệ số a dương(a > 0) thì góc αtạo bởi đường thẳng y = ax + b và trục Ox là góc nhọn. Hệ số a càng lớn thì góc αcàng lớn nhưng vẫn nhỏ hơn 90°.

− Khi hệ số a âm (a < 0) thì góc β tạo bởi đường thẳng y = ax + b (a ≠ 0) và trục Ox là góc tù. Hệ số a càng lớn thì gócβ càng lớn nhưng vẫn nhỏ hơn 180°.

• Hệ số a là hệ số góc của đường thẳng y = ax + b (a ≠ 0).

9. Hai đường thẳng song song, hai đường thẳng cắt nhau

9.1. Nhận biết hai đường thẳng song song

• Hai đường thẳng phân biệt có hệ số góc bằng nhau thì song song với nhau và ngược lại, hai đường thẳng song song thì có hệ số góc bằng nhau.

Chú ý: Hai đường thẳng y = ax + b và y = a'x + b' trùng nhau khi và chỉ khi a = a', b = b'.

• Hai đường thẳng d: y = ax + b (a ≠ 0) và d': y = a'x + b' (a' ≠ 0) cắt nhau khi a ≠ a' và ngược lại.

9.2. Nhận biết hai đường thẳng cắt nhau

Hai đường thẳng có hệ số góc khác nhau thì cắt nhau và ngược lại, hai đường thẳng cắt nhau thì có hệ số góc khác nhau.

Bài tập tổng hợp Toán 8 Chương 5

Bài 1. Các giá trị tương ứng của hai đại lượng x và y được cho bởi các bảng sau. Đại lượng y có phải là hàm số của đại lượng x không?

a)

b)

x	3	2	1	0	3
y	2	1	3	4	5

Hướng dẫn giải

a) Đại lượng y là hàm số của đại lượng x vì mỗi giá trị của x chỉ xác định đúng một giá trị của y.

b) Đại lượng y không là hàm số của đại lượng x vì với giá trị x = 3 thì y nhận hai giá trị là 2 và 5.

Bài 2. Thời gian t (giờ) của một vật chuyển động đều trên quãng đường 20 km tỉ lệ nghịch với tốc độ v (km/h) của nó theo công thức $t=\frac{20}{v}$. Đại lượng t có phải là hàm số của đại lượng v hay không? Nếu có, tính thời gian chuyển động của vật đó biết tốc độ của vật là 40 km/h?

Hướng dẫn giải

Đại lượng t là hàm số của đại lượng v vì mỗi giá trị của v ta nhận được chỉ một giá trị của t.

Với v = 40km/h thì t$=\frac{20}{40}=\frac{1}{2}$ (giờ).

Bài 3. Cho hàm số y = f(x) = 3x. Tính f(1); f(−2); f$\left(\frac{1}{3}\right)$.

Hướng dẫn giải

f(1) = 3.1 = 3; f(−2) = 3.(−2) = −6 ; f$\left(\frac{1}{3}\right)$= 3.$\frac{1}{3}$= 1.

Bài 4. Cho hàm số y = f(x) = −mx + m – 3. Biết f(−2) = 6, tính f(−3).

Hướng dẫn giải

Ta có f(−2) = 6

−m . (−2) + m – 3 = 6

3m = 9

m = 3

Khi đó f(x) = −3x nên f(−3) = 9.

Bài 5. Giá cước taxi của một hãng xe khi quãng đường di chuyển x (km) khoảng từ 1 km đến 30 km được cho bởi công thức sau:

T(x) = 10 000 + 13 600(x – 1) (đồng).

a) Tính số tiền phải trả khi xe di chuyển 20 km.

b) Nếu một hành khách phải trả 200 400 đồng thì hành khách đó đã di chuyển bao nhiêu kilômét?

Hướng dẫn giải

a) Khi x = 20 thì T(20) = 10 000 + 13 600 ∙ (20 – 1) = 268 400.

Vậy khi xe di chuyển 20 km thì số tiền phải trả là 268 400 đồng.

b) Theo đề bài, ta có T(x) = 200 400

10 000 + 13 600∙ (x – 1) = 200 400

13 600∙ (x – 1) = 190 400

x – 1 = 14

x = 15.

Vậy nếu một hành khách phải trả 200 400 đồng thì hành khách đó đã di chuyển 15 km.

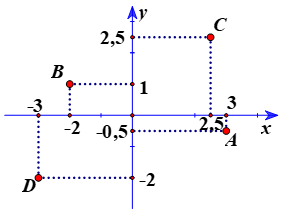
Bài 6. Vẽ mặt phẳng tọa độ Oxy và đánh dấu vị trí các điểm sau trên đó A(3; −0,5), B(−2; 1), C(2,5; 2,5), D(−3; −2).

Hướng dẫn giải

Cách xác định:

− Từ điểm biểu diễn hoành độ của điểm cho trước, kẻ một đường thẳng song song với trục tung.

− Tử điểm biểu diễn tung độ của điểm cho trước, kẻ một đường thẳng song song với trục hoành.

− Giao điểm của hai đường thẳng vừa dựng là điểm phải tìm.

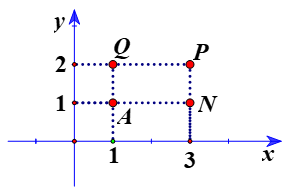
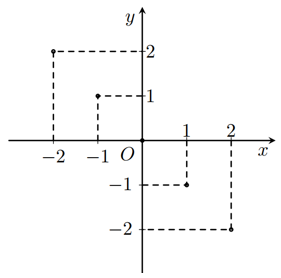
Bài 7.Viết tọa độ các điểm A, N, P, Q trong hình bên dưới.

Hướng dẫn giải

Cách xác định:

− Từ điểm đã cho kẻ đường thẳng song song với trục tung, cắt trục hoành tại một điểm biểu diễn hoành độ của điểm đó.

− Từ điểm đã cho kẻ đường thẳng song song với trục hoành, cắt trục tung tại một điểm biểu diễn tung độ của điểm đó.

− Hoành độ và tung độ tìm được là tọa độ của điểm đã cho.

Từ đó, ta các định được tọa độ các điểm là: A(1;1), N(3;1), P(3;2), Q(1; 2).

Bài 8. Vẽ đồ thị của hàm số y = f(x) cho bằng bảng sau:

Hướng dẫn giải

Đồ thị hàm số là tập hợp các điểm có tọa độ (−2; 2), (−1; 1), (0; 0), (1; −1), (2; −2).

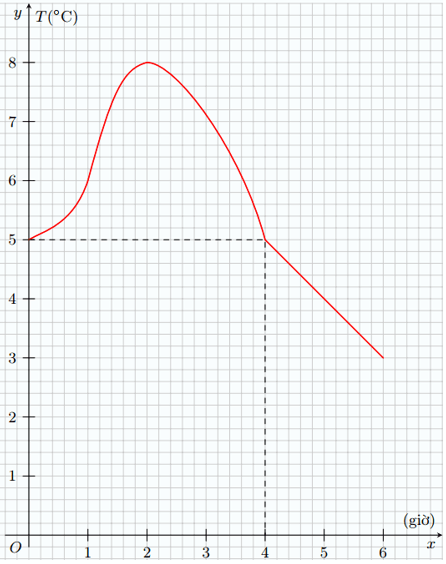
Bài 9. Hình sau là đồ thị của hàm số mô tả nhiệt độ T(°C) tại các thời điểm t (giờ) của một thành phố ở châu Âu từ giữa trưa đến 6 giờ tối.

a) Tìm T(1), T(2), T(5) và giải thích ý nghĩa của số này.

b) Trong hai giá trị T(1) và T(4), giá trị nào lớn hơn?

c) Tìm t sao cho T(t) = 5.

d) Trong khoảng thời gian nào thì nhiệt độ cao hơn 5°C?

Hướng dẫn giải

a) Ta có T(1) = 6; T(2) = 8, T(5) = 4. Nghĩa là nhiệt độ vào lúc 1 giờ, 2 giờ, 5 giờ ở thành phố đó lần lượt là 6°C, 8°C, 4°C.

b) Ta có T(1) = 6 và T(4) = 5 nên T(1) < T(4).

c) Dựa vào đồ thị, ta có T(t) = 5 khi t = 0 hoặc t = 4.

d) Dựa vào đồ thị, trong khoảng thời gian từ sau 12 giờ trưa đến trước 4 giờ chiều thì nhiệt độ ở thành phố đó cao hơn 5°C.

Bài 10. Trong hai hàm số y = 3x + 1 và y = 0x + 3, hàm số nào là hàm số bậc nhất? Vì sao?

Hướng dẫn giải

Trong hai hàm số đã cho, chỉ có hàm số y = 3x + 1 là hàm số bậc nhất vì thỏa mãn cả hai điều kiện là dạng hàm số y = ax + b và a ≠ 0.

Hàm số y = 0x + 3 có dạng y = ax + b nhưng với a = 0 nên không phải hàm số bậc nhất.

Bài 11. Cho hàm số bậc nhất f(x) = x − 1. Tính f (1); f(0); f(−2).

Hướng dẫn giải

f(1) = 1 −1 = 0; f(0) = 0 −1 = −1; f(−2) = −2 −1 = −3.

Vậy f(1) = 0; f(0) = −1; f(−2) = −3.

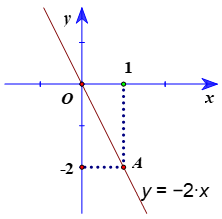
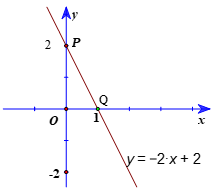
Bài 12. Vẽ đồ thị của các hàm số sau:

a) y = −2x.

b) y = −2x + 2.

Hướng dẫn giải

a) Với x = 1 thì y = −2, ta được A(1; −2) thuộc đồ thị hàm số y = −2x.

Vậy đồ thị của hàm số y = −2x là đường thẳng đi qua hai điểm O(0; 0) và A(1; −2).

b) Với x = 0 thì y = 2, ta được điểm P(0; 2) thuộc đồ thị của hàm số y = −2x + 2.

Với y = 0 thì x = 1, ta được điểm Q(1; 0) thuộc đồ thị của hàm số y = −2x + 2.

Vẽ đồ thị của hàm số y = −2x + 2 là đường thẳng đi qua hai điểm P(0; 2), Q(1; 0).

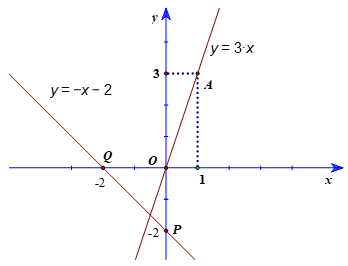
Bài 13. Vẽ đồ thị của các hàm số y = 3x; y = −x − 2 trên cùng một mặt phẳng tọa độ?

Hướng dẫn giải

• Với x = 1 thì y = 3, ta được điểm A(1; 3) thuộc đồ thị hàm số y = 3x.

Vẽ đồ thị hàm số y = 3x là đường thẳng đi qua gốc tọa độ và điểm A.

• Với x = 0 thì y = −2, ta được điểm P(0; −2) thuộc đồ thị hàm số y = −x − 2.

Với y = 0 thì x = −2, ta được điểm Q(−2; 0) thuộc đồ thị hàm số y = −x − 2.

Vẽ đồ thị hàm số y = −x – 2 là đường thẳng đi qua hai điểm P và Q.

Bài 14. Giá bán 1 kg vải thiều loại I là 35 000 đồng.

a) Viết công thức biểu thị số tiền y (đồng) thu được khi bán x kg vải thiều loại I. Hỏi y có phải là hàm số bậc nhất của x hay không?

b) Tính số tiền thu được khi bán 15 kg vải thiều loại I?

c) Cần bán bao nhiêu kg vải thiều loại I để thu được số tiền 1 400 000 đồng?

Hướng dẫn giải

a) Công thức biểu thị số tiền y (đồng) thu được khi bán x kg vải thiều loại I là:

y = 35 000x.

Do đó y là hàm số bậc nhất của x.

b) Số tiền thu được khi bán 15 kg vải thiều loại I là:

35 000 . 15 = 525 000 (đồng).

Vậy số tiền thu được khi bán 15 kg vải thiều loại I là 525 000 đồng.

c) Số kg vải thiều loại I để thu được số tiền 1 400 000 đồng là:

1 400 000 : 35 000 = 40 (kg).

Vậy cần bán 40 kg vải thiều loại I để thu được số tiền 1 400 000 đồng.

Bài 15. Giá cước điện thoại cố định của một hãng viễn thông bao gồm cước thuê bao là 22000 đồng/tháng và cước gọi là 800 đồng/phút.

a) Lập công thức tính số tiền cước điện thoại y (đồng) phải trả trong tháng khi gọi x phút?

b) Tính số tiền cước điện thoại phải trả khi gọi 75 phút?

c) Nếu số tiền cước điện thoại phải trả là 94 000 đồng thì trong tháng đó thuê bao đã gọi bao nhiêu phút?

Hướng dẫn giải

a) Công thức tính số tiền cước điện thoại y (đồng) phải trả trong tháng khi gọi x phút là: y = 800x + 22 000.

b) Số tiền cước điện thoại phải trả khi gọi 75 phút là:

y = 800 . 75 + 22 000 = 82 000 (đồng).

Vậy số tiền cước điện thoại phải trả khi gọi 75 phút là 82 000 đồng.

c) Số tiền cước điện thoại phải trả là 94 000 đồng thì trong tháng đó thuê bao đã gọi số phút là:

94 000 = 800x + 22 000

800x = 94 000 − 22 000

800x = 72 000

x = 90.

Vậy nếu số tiền cước điện thoại phải trả là 94 000 đồng thì trong tháng đó thuê bao đã gọi 90 phút.

Bài 16. Chỉ ra các cặp đường thẳng cắt nhau và các cặp đường thẳng song song trong các đường thẳng sau: y = 3x + 1; y = 3x; y = −2x – 2.

Hướng dẫn giải

• Cặp đường thẳng song song là: y = 3x + 1; y = 3x.

•Cặp đường thẳng cắt nhau là: y = 3x + 1 và y = −2x – 2; y = 3x và y = −2x – 2.

Bài 17. Cho đồ thị của hàm số bậc nhất y = mx + 3 và y = (2m – 2)x + 5. Với giá trị nào của m thì hai đường thẳng này cắt nhau?

Hướng dẫn giải

Hai đường thẳng trên là đồ thị của hàm số bậc nhất nên m ≠ 0 và 2m – 2 ≠ 0 hay m ≠ 0 và m ≠ 1.

Hai đường thẳng trên cắt nhau khi m ≠ 2m – 2 hay m ≠ 2.

Bài 18. Tìm hàm số bậc nhất có đồ thị là đường thẳng có hệ số góc a = 2 và đi qua điểm (0; 1).

Hướng dẫn giải

Hàm số bậc nhất có dạng y = 2x + b.

Hàm số đi qua điểm (0; 1) nên 1 = 2 . 0 + b hay b = 1 – 2 . 0 = 1.

Vậy hàm số cần tìm là y = 2x + 1.

Bài 19.

a) Xác định đường thẳng y = ax + b (a ≠ 0) có hệ số góc bằng −1 và đi qua điểm M(1; 2).

b) Xác định đường thẳng y = ax + b (a ≠ 0) đi qua điểm M(1; 3) và song song với đường thẳng y = 2x.

Hướng dẫn giải

a) Vì đường thẳng y = ax + b (a ≠ 0) có hệ số góc bằng −1 nên đường thẳng có dạng

y = −x + b.

Vì đường thẳng y = −x + b đi qua điểm M(1; 2) nên ta có: 2 = −1 + b, suy ra b = 3.

Vậy y = −x + 3.

b) Vì đường thẳng y = ax + b (a ≠ 0) song song với đường thẳng y = 2x nên đường thẳng có dạng: y = 2x + b.

Mà đường thẳng y = 2x + b đi qua điểm M(1; 3) nên 3 = 2.1 + b, suy ra b = 1.

Vậy y = 2x +1.

Bài 20. Tìm tọa độ giao điểm của hai đường thẳng y = 2x + 5 và y = 3x + 1.

Hướng dẫn giải

Phương trình tọa độ giao điểm của hai đường thẳng là

2x + 5 = 3x + 1

3x – 2x = 5 – 1

x = 4

Với x = 4, ta có y = 2 . 4 + 5 = 13.

Vậy tọa độ giao điểm của hai đường thẳng là (4; 13).

Học tốt Toán 8 Chương 5

Các bài học để học tốt Chương 5 Toán lớp 8 hay khác:

• Giải sgk Toán 8 Bài tập cuối chương 5

(199k) Xem Khóa học Toán 8 CTST

Xem thêm tóm tắt lý thuyết Toán lớp 8 Chân trời sáng tạo hay khác:

• Lý thuyết Toán 8 Bài 4: Hệ số góc của đường thẳng

• Lý thuyết Toán 8 Bài 1: Phương trình bậc nhất một ẩn

• Lý thuyết Toán 8 Bài 2: Giải bài toán bằng cách lập phương trình bậc nhất

• Tổng hợp lý thuyết Toán 8 Chương 6

• Lý thuyết Toán 8 Bài 1: Định lí Thalès trong tam giác

• Lý thuyết Toán 8 Bài 2: Đường trung bình của tam giác

Xem thêm các tài liệu học tốt lớp 8 hay khác:

• Giải sgk Toán 8 Chân trời sáng tạo
• Giải SBT Toán 8 Chân trời sáng tạo
• Giải lớp 8 Chân trời sáng tạo (các môn học)
• Giải lớp 8 Kết nối tri thức (các môn học)
• Giải lớp 8 Cánh diều (các môn học)

---