15 dạng bài Đường thẳng và mặt phẳng trong không gian chọn lọc
15 dạng bài Đường thẳng và mặt phẳng trong không gian chọn lọc
(199k) Xem Khóa học Toán 11 KNTTXem Khóa học Toán 11 CDXem Khóa học Toán 11 CTST
Phần Đường thẳng và mặt phẳng trong không gian Toán lớp 11 sẽ tổng hợp Lý thuyết, các dạng bài tập chọn lọc có trong Đề thi THPT Quốc gia và trên 200 bài tập trắc nghiệm chọn lọc, có lời giải. Vào Xem chi tiết để theo dõi các dạng bài Đường thẳng và mặt phẳng trong không gian tương ứng.
Tổng hợp lý thuyết chương Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
- Lý thuyết Đại cương về đường thẳng và mặt phẳng
- Lý thuyết Hai đường thẳng chéo nhau và hai đường thẳng song song
- Lý thuyết Đường thẳng và mặt phẳng song song
- Lý thuyết Hai mặt phẳng song song
- Lý thuyết Phép chiếu song song. Hình biểu diễn của một hình không gian
- Lý thuyết Tổng hợp chương Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
Các dạng bài tập
- Đại cương về đường thẳng và mặt phẳng và cách giải
- Hai đường thẳng song song trong không gian và cách giải
- Đường thẳng song song với mặt phẳng và cách giải bài tập
- Hai mặt phẳng song song và cách giải bài tập
- Câu hỏi trắc nghiệm lý thuyết về đường thẳng và mặt phẳng Xem chi tiết
- Cách tìm giao tuyến của hai mặt phẳng Xem chi tiết
- Cách tìm giao điểm của đường thẳng và mặt phẳng Xem chi tiết
- Cách tìm thiết diện của hình chóp Xem chi tiết
- Cách chứng minh 3 điểm thẳng hàng, 3 đường thẳng đồng quy Xem chi tiết
- Cách tìm quỹ tích giao điểm của hai đường thẳng Xem chi tiết
- Câu hỏi trắc nghiệm lý thuyết về hai đường thẳng song song trong không gian Xem chi tiết
- Cách chứng minh hai đường thẳng song song trong không gian Xem chi tiết
- Cách chứng minh 4 điểm đồng phẳng, 3 đường thẳng đồng quy Xem chi tiết
- Cách tìm giao tuyến của 2 mặt phẳng chứa 2 đường thẳng song song Xem chi tiết
- Tìm thiết diện của hình chóp cắt bởi mặt phẳng chứa đường thẳng song song với đường thẳng khác Xem chi tiết
- Câu hỏi trắc nghiệm lý thuyết về đường thẳng song song với mặt phẳng Xem chi tiết
- Cách chứng minh đường thẳng song song với mặt phẳng Xem chi tiết
- Tìm giao tuyến của 2 mặt phẳng. Tìm thiết diện qua 1 điểm và song song với đường thẳng Xem chi tiết
- Câu hỏi trắc nghiệm lý thuyết hai mặt phẳng song song Xem chi tiết
- Cách chứng minh hai mặt phẳng song song Xem chi tiết
- Tìm giao tuyến của 2 mặt phẳng. Thiết diện qua 1 điểm song song với mặt phẳng Xem chi tiết
- 22 câu hỏi trắc nghiệm Phép chiếu song song chọn lọc có đáp án Xem chi tiết
Cách tìm giao tuyến của hai mặt phẳng
A. Phương pháp giải
Muốn tìm giao tuyến của hai mặt phẳng: ta tìm hai điểm chung thuộc cả hai mặt phẳng. Nối hai điểm chung đó được giao tuyến cần tìm.
Về dạng này điểm chung thứ nhất thường dễ tìm. Điểm chung còn lại các bạn phải tìm hai đường thẳng lần lượt thuộc hai mặt phẳng, đồng thời chúng lại thuộc mặt phẳng thứ ba và chúng không song song. Giao điểm của hai đường thẳng đó là điểm chung thứ hai.
Chú ý: Giao tuyến là đường thẳng chung của hai mặt phẳng, có nghĩa là giao tuyến là đường thẳng vừa thuộc mặt phẳng này vừa thuộc mặt phẳng kia.
B. Ví dụ minh họa
Ví dụ 1: Cho hình chóp S.ABCD có đáy là hình thang, đáy lớn AB. Gọi O là giao điểm của AC và BD; I là giao điểm của AD và BC. Tìm mệnh đề sai?
A. Hình chóp S.ABCD có 4 mặt bên.
B. Giao tuyến của hai mặt phẳng (SAC) và (SBD) là SO.
C. Giao tuyến của hai mặt phẳng (SAD) và (SBC) là SI.
D. Đường thẳng SO nhìn thấy nên được biểu diễn bằng nét đứt.
Lời giải
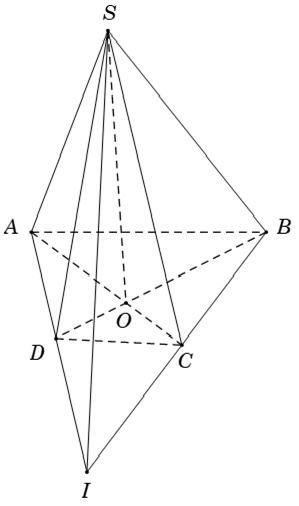
Xét các phương án:
+ Phương án A:
Hình chóp S.ABCD có 4 mặt bên là: (SAB); (SBC); (SCD) và (SAD). Do đó A đúng.
+ Phương án B:
Ta có:
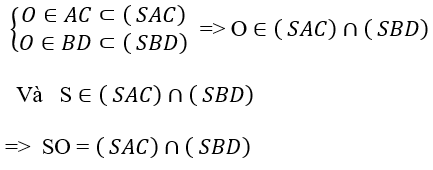
Do đó B đúng
+ Tương tự, ta có SI = (SAD) ∩ (SBC). Do đó C đúng.
+ Đường thẳng SO không nhìn thấy nên được biểu diễn bằng nét đứt. Do đó D sai. Chọn D.
Ví dụ 2: Cho tứ giác ABCD sao cho các cạnh đối không song song với nhau. Lấy một điểm S không thuộc mặt phẳng (ABCD). Xác định giao tuyến của mặt phẳng (SAC) và mặt phẳng (SBD).
A. SO trong đó O là giao điểm của AC và BD.
B. SI trong đó I là giao điểm của AB và CD.
C. SE trong đó E là giao điểm của AD và BC.
D. Đáp án khác
Lời giải
+ Ta có : S ∈ (SAC) ∩ (SBD) (1)
+ Trong mp(ABCD) gọi giao điểm của AC và BD là O. ( bạn đọc tự vẽ hình)
- Vì
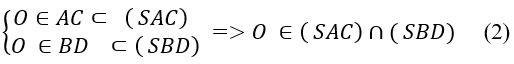
+ Từ (1) và (2) suy ra SO = (SAC) ∩ (SBD)
Chọn A
Ví dụ 3: Cho tứ giác ABCD sao cho các cạnh đối không song song với nhau. Lấy một điểm S không thuộc mặt phẳng (ABCD). Xác định giao tuyến của mặt phẳng (SAB) và mặt phẳng (SCD)
A. SO trong đó O là giao điểm của AC và BD
B. SI trong đó I là giao điểm của AB và CD
C. SE trong đó E là giao điểm của AD và BC
D. Đáp án khác
Lời giải
+ Ta có: S ∈ (SAB) ∩ (SCD) (1)
+ Trong mp(ABCD) gọi giao điểm của AB và CD là I. (bạn đọc tự vẽ hình)
Vì
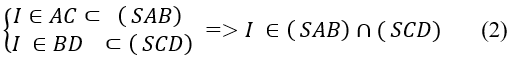
+ Từ (1) và (2) suy ra SI = (SAB) ∩ (SCD)
Chọn B
Cách chứng minh 3 điểm thẳng hàng, 3 đường thẳng đồng quy
A. Phương pháp giải
- Để chứng minh 3 điểm A; B; C thẳng hàng ta chứng minh 3 điểm đó cùng thuộc 1 đường thẳng hoặc chứng minh 3 điểm đó là điểm chung của hai mặt phẳng (α) và (β) - Khi đó chúng cùng thuộc giao tuyến của 2 mặt phẳng (α) và (β).
- Để chứng minh ba đường thẳng đồng quy ta có thể làm theo những cách sau:
+ Cách 1: chứng minh giao điểm của hai đường này là điểm chung của hai mặt phẳng mà giao tuyến là đường thẳng thứ ba
+ Cách 2: Dựa vào định lí: Ba mặt phẳng phân biệt cắt nhau theo ba giao tuyến khi đó; ba giao tuyến đó đồng quy hoặc đôi một song song
B. Ví dụ minh họa
Ví dụ 1: Cho tứ diện ABCD. Gọi M; N lần lượt là trung điểm của AB và CD. Mặt phẳng (P) qua MN và cắt AD; BC lần lượt tại P và Q. Biết MP cắt NQ tại I. Ba điểm nào sau đây thẳng hàng?
A. I; A; C B. I; B; D C. I; A; B D. I; C; D
Lời giải
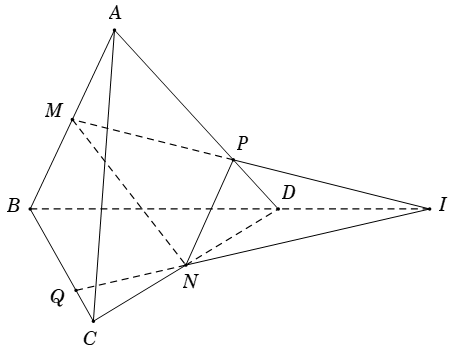
Ta có: (ABD) ∩ (BCD) = BD (1)
Lại có
Từ (1) và (2) suy ra: I ∈ BD hay 3 điểm I; B; D thẳng hàng
Chọn B
Ví dụ 2: Cho tứ diện SABC. Gọi L; M; N lần lượt là các điểm trên các cạnh SA; SB và AC sao cho LM không song song với AB và LN không song song với SC. Mặt phẳng (LMN) cắt các cạnh AB; BC và SC lần lượt tại K; I; J. Ba điểm nào sau đây thẳng hàng?
A. K; I và J B. M; I và J C. N ; I và J D. M; K và J
Lời giải
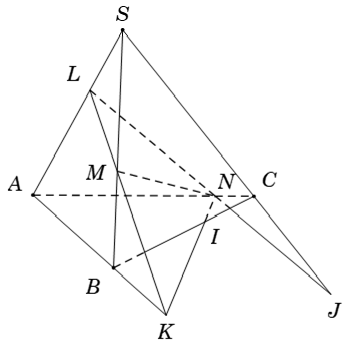
Ta có
- M ∈ SB suy ra M isin; (LMN) ∩ (SBC) (1)
- I ∈ BC ⊂ (SBC) và I ∈ NK ⊂ (LMN)
⇒ I ∈ (LMN) ∩ (SBC) (2)
- J ∈ SC ⊂ (SBC) và J ∈ LN ⊂ (LMN)
⇒ J ∈ (LMN) ∩ (SBC) (3)
Vậy M ; I; J thẳng hàng vì cùng thuộc giao tuyến của mp (LMN) và (SBC)
Chọn B
Ví dụ 3: Cho tứ diện ABCD. Gọi G là trọng tâm tam giác BCD; M là trung điểm CD; I thuộc đoạn AG; BI cắt mp (ACD) tại J. Chọn mệnh đề sai
A. Giao tuyến của (ACD) và (ABG) là AM
B. 3 điểm A; J; M thẳng hàng.
C. J là trung điểm của AM.
D. Giao tuyến của mp(ACD) và (BDJ) là DJ.
Lời giải
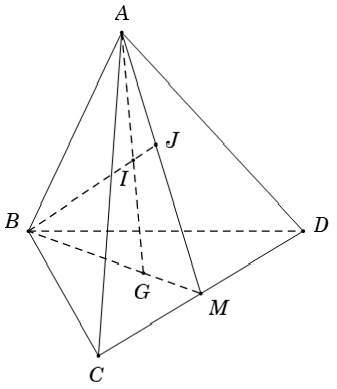
Ta xét các phương án:
+ Ta có: A là điểm chung thứ nhất giữa hai mp (ACD) và mp (GAB) (1)
Do M là giao điểm của BG và CD nên:
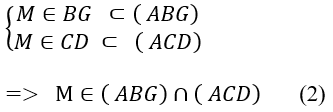
Từ (1) và (2) suy ra: giao tuyến của (ABG) và (ACD) là AM ⇒ A đúng
+ Ta có 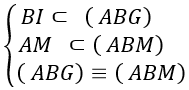
⇒ J = BI ∩ AM nên 3 điểm A; J; M thẳng hàng → B đúng.
+ Ta có
⇒ D đúng
+ Điểm I di động trên AG nên J có thể không phải là trung điểm của AM.
⇒ C sai
Chọn C
Cách chứng minh hai đường thẳng song song trong không gian
A. Phương pháp giải
Để chứng ming hai đường thẳng song song trong không gian có thể sử dụng 1 trong các cách sau:
1. Chứng minh 2 đường thẳng đó đồng phẳng, rồi áp dụng phương pháp chứng minh song song trong hình học phẳng (như tính chất đường trung bình, định lí Talét đảo, …)
2. Chứng minh 2 đường thẳng đó cùng song song với đường thẳng thứ ba.
3. Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
4. Áp dụng định lí về giao tuyến song song.
B. Ví dụ minh họa
Ví dụ 1: Cho tứ diện ABCD. Gọi I và J lần lượt là trọng tâm các tam giác ABC và ABD. Chọn mệnh đề đúng.
A. IJ // CD
B. IJ // AB
C. IJ và CD chéo nhau
D. IJ cắt AB
Lời giải
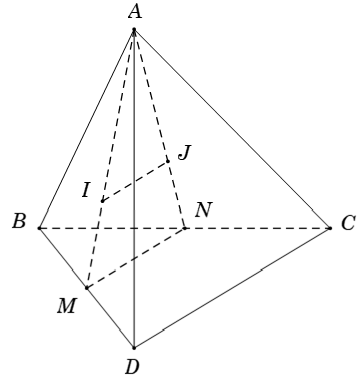
+ Gọi M và N lần lượt là trung điểm của BC và BD
⇒ MN là đường trung bình của tam giác BCD nên MN // CD (1)
+ Do I và J lần lượt là trọng tâm các tam giác ABC và ABD
⇒ AI/AM = AJ/AN = 2/3
⇒ IJ // MN (định lí Ta-let đảo) (2)
Từ (1) và (2) suy ra: IJ // CD
Chọn A
Ví dụ 2: Cho hình chóp S. ABCD có AD không song song với BC. Gọi M; N; P; Q; R; T lần lượt là trung điểm của AC; BD; BC; CD; SA và SD. Hai đường thẳng nào sau đây song song với nhau.
A. MP và RT
B. MQ và RT
C. MN và RT
D. PQ và RT
Lời giải
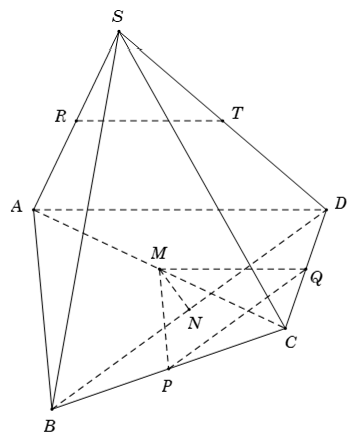
+ Ta có: M và Q lần lượt là trung điểm của AC; CD
⇒ MQ là đường trung bình của tam giác CAD nên MQ // AD (1)
+ Ta có: R; T lần lượt là trung điểm của SA; SD
⇒ RT là đường trung bình của tam giác SAD nên RT // AD (2)
+ Từ (1) và ( 2) suy ra: MQ // RT
Chọn B
Ví dụ 3: Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi I; J; E; F lần lượt là trung điểm của SA; SB; SC và SD. Tìm đường thẳng không song song với IJ trong các đường thẳng sau:
A. EF B. DC C. AD D. AB
Lời giải
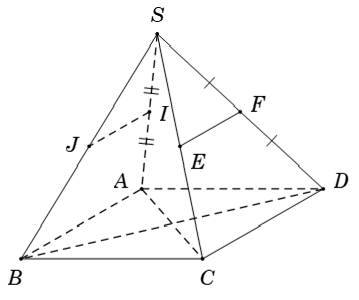
+ Xét tam giác SAB có IJ là đường trung bình
⇒ IJ // AB (tính chất đường trung bình trong tam giác) (1)
+ Xét tam giác SCD có EF là đường trung bình
⇒ EF // CD (2)
+ Mà ABCD là hình bình hành nên : AB// CD (3)
Từ( 1); (2) và (3) suy ra: IJ // AB // CD // EF
Chọn C
(199k) Xem Khóa học Toán 11 KNTTXem Khóa học Toán 11 CDXem Khóa học Toán 11 CTST
Xem thêm các dạng bài tập Toán lớp 11 có trong đề thi THPT Quốc gia khác:
- Chuyên đề: Hàm số lượng giác - phương trình lượng giác
- Chuyên đề: Tổ hợp - Xác suất
- Chuyên đề: Dãy số - Cấp số cộng và cấp số nhân
- Chuyên đề: Giới hạn
- Chuyên đề: Đạo hàm
- Chuyên đề: Phép dời hình và phép đồng dạng trong mặt phẳng
- Chuyên đề: Vectơ trong không gian. Quan hệ vuông góc trong không gian
Tủ sách VIETJACK shopee lớp 10-11 (cả 3 bộ sách):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 11 Global Success
- Giải sgk Tiếng Anh 11 Smart World
- Giải sgk Tiếng Anh 11 Friends Global
- Lớp 11 - Kết nối tri thức
- Soạn văn 11 (hay nhất) - KNTT
- Soạn văn 11 (ngắn nhất) - KNTT
- Giải sgk Toán 11 - KNTT
- Giải sgk Vật Lí 11 - KNTT
- Giải sgk Hóa học 11 - KNTT
- Giải sgk Sinh học 11 - KNTT
- Giải sgk Lịch Sử 11 - KNTT
- Giải sgk Địa Lí 11 - KNTT
- Giải sgk Giáo dục KTPL 11 - KNTT
- Giải sgk Tin học 11 - KNTT
- Giải sgk Công nghệ 11 - KNTT
- Giải sgk Hoạt động trải nghiệm 11 - KNTT
- Giải sgk Giáo dục quốc phòng 11 - KNTT
- Giải sgk Âm nhạc 11 - KNTT
- Lớp 11 - Chân trời sáng tạo
- Soạn văn 11 (hay nhất) - CTST
- Soạn văn 11 (ngắn nhất) - CTST
- Giải sgk Toán 11 - CTST
- Giải sgk Vật Lí 11 - CTST
- Giải sgk Hóa học 11 - CTST
- Giải sgk Sinh học 11 - CTST
- Giải sgk Lịch Sử 11 - CTST
- Giải sgk Địa Lí 11 - CTST
- Giải sgk Giáo dục KTPL 11 - CTST
- Giải sgk Hoạt động trải nghiệm 11 - CTST
- Giải sgk Âm nhạc 11 - CTST
- Lớp 11 - Cánh diều
- Soạn văn 11 Cánh diều (hay nhất)
- Soạn văn 11 Cánh diều (ngắn nhất)
- Giải sgk Toán 11 - Cánh diều
- Giải sgk Vật Lí 11 - Cánh diều
- Giải sgk Hóa học 11 - Cánh diều
- Giải sgk Sinh học 11 - Cánh diều
- Giải sgk Lịch Sử 11 - Cánh diều
- Giải sgk Địa Lí 11 - Cánh diều
- Giải sgk Giáo dục KTPL 11 - Cánh diều
- Giải sgk Tin học 11 - Cánh diều
- Giải sgk Công nghệ 11 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 11 - Cánh diều
- Giải sgk Giáo dục quốc phòng 11 - Cánh diều
- Giải sgk Âm nhạc 11 - Cánh diều

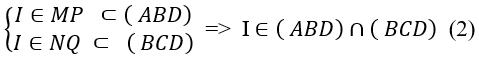
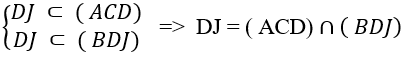



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

