Các số đặc trưng đo mức độ phân tán của mẫu số liệu ghép nhóm lớp 12 (Chuyên đề dạy thêm Toán 12)

Tài liệu Chuyên đề Các số đặc trưng đo mức độ phân tán của mẫu số liệu ghép nhóm lớp 12 trong Chuyên đề dạy thêm Toán 12 gồm các dạng bài tập từ cơ bản đến nâng cao với phương pháp giải chi tiết và bài tập tự luyện đa dạng giúp Giáo viên có thêm tài liệu giảng dạy Toán 12.

Các số đặc trưng đo mức độ phân tán của mẫu số liệu ghép nhóm lớp 12 (Chuyên đề dạy thêm Toán 12)

Xem thử

Chỉ từ 400k mua trọn bộ Chuyên đề dạy thêm Toán 12 (sách mới) bản word có lời giải chi tiết:

• B1: gửi phí vào tk: 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án

A. Kiến thức cần nhớ

1. Khoảng biến thiên

a) Định nghĩa

▪ Khoảng biến thiên, kí hiệu R, của mẫu số liệu ghép nhóm là hiệu số giữa đầu mút phải của nhóm cuối cùng và đầu mút trái của nhóm đầu tiên có chứa dữ liệu của mẫu số liệu.

Chẳng hạn: Xét mẫu số liệu ghép nhóm được cho ở bảng sau: (Bảng 1)

Nhóm	[u1;u2)	[u2;u3)	…	[uk;uk+1)
Tần số	n1	n2	…	nk

▪ Nếu n₁ và n_k cùng lớn hơn 0 thì R = u_k+1 - u₁

▪ Khoảng biến thiên của mẫu số liệu ghép nhóm luôn lớn hơn hoặc bằng khoảng biến thiên của mẫu số liệu gốc.

b) Ý nghĩa của khoảng biến thiên của mẫu số liệu ghép nhóm

▪ Khoảng biến thiên của mẫu số liệu ghép nhóm là giá trị xấp xỉ khoảng biến thiên của mẫu số liệu gốc và có thể dùng để đo mức độ phân tán của mẫu số liệu. Khoảng biến thiên càng lớn thì mẫu số liệu càng phân tán.

▪ Khoảng biến thiên R = u_k+1 - u₁ chưa phản ánh được đầy đủ mức độ phân tán của phần lớn các số liệu. Hơn nữa, giá trị của R thường tăng vọt khi xuất hiện giá trị bất thường (còn gọi là giá trị ngoại lệ) trong mẫu số liệu. Do đó, để phản ánh mức độ phân tán của số liệu, người ta còn dùng các số đặc trưng khác.

2. Khoảng tứ phân vị

a) Định nghĩa

Xét mẫu số liệu ghép nhóm được cho ở bảng sau: (Bảng 1)

Nhóm	[u1;u2)	[u2;u3)	…	[uk;uk+1)
Tần số	n1	n2	…	nk

▪ Tứ phân vị thứ k, kí hiệu là Q_k, với k = 1, 2, 3 của mẫu số liệu ghép nhóm (Bảng 1) được xác định như sau: $Q_k=u_m+\frac{\frac{kn}{4}-C}{n_m}(u_{m+1}-u_m)$, trong đó:

• n = n₁ + n₂ + ... + n_k là cỡ mẫu;

• [u_m;u_m+1) là nhóm chứa tứ phân vị thứ k;

• n_m là tần số của nhóm chứa tứ phân vị thứ k;

• C = n₁ + n₂ + ... + n_m+1

▪ Nếu tứ phân vị thứ k là $\frac{1}{2}\left(x_m+x_{m+1}\right)$, trong đó x_m và x_m+1 thuộc hai nhóm liên tiếp, ví dụ như x_m ∈ [u_j-1;u_j) và x_m+1 ∈ [u_j;u_j+1) thì ta lấy Q_k = u_j

▪ Khoảng tứ phân vị của mẫu số liệu ghép nhóm cũng được xác định dựa trên tứ phân vị thứ nhất và tứ phân vị thứ ba như đối với mẫu số liệu không ghép nhóm.

▪ Khoảng tứ phân vị của mẫu số liệu ghép nhóm cho ở Bảng 1, kí hiệu ∆_Q, là hiệu giữa tứ phân vị thứ ba Q₃ và tứ phân vị thứ nhất Q₁ của mẫu số liệu ghép nhóm đó, tức là

∆_Q = Q₃ – Q₁.

b) Ý nghĩa của khoảng tứ phân vị của mẫu số liệu ghép nhóm

▪ Khoảng tứ phân vị của mẫu số liệu ghép nhóm là giá trị xấp xỉ cho khoảng tứ phân vị của mẫu số liệu gốc và có thể dùng để đo mức độ phân tán của nửa giữa của mẫu số liệu (tập hợp gồm 50% số liệu nằm chính giữa mẫu số liệu).

▪ Khoảng tứ phân vị của mẫu số liệu ghép nhóm càng nhỏ thì dữ liệu càng tập trung xung quanh trung vị.

▪ Khoảng tứ phân vị được dùng để xác định giá trị bất thường (giá trị ngoại lệ) trong mẫu số liệu. Giá trị x trong mẫu số liệu là giá trị ngoại lệ nếu x > Q₃ + 1,5∆_Q hoặc x < Q₁ − 1,5∆_Q.

▪ Khoảng tứ phân vị của mẫu số liệu ghép nhóm không bị ảnh hưởng nhiều bởi các giá trị bất thường (giá trị ngoại lệ) trong mẫu số liệu.

3. Một số kiến thức bổ trợ quan trọng

⮚ Một số quy tắc ghép nhóm của mẫu số liệu

▪ Mỗi mẫu số liệu có thể được ghép nhóm theo nhiều cách khác nhau nhưng thường tuân theo một số quy tắc sau:

▪ Sử dụng từ k = 5 đến k = 20 nhóm. Cỡ mẫu càng lớn thì cần càng nhiều nhóm số liệu.

▪ Các nhóm có cùng độ dài bằng L thoả mãn R < k.L, trong đó R là khoảng biến thiên, k là số nhóm.

▪ Giá trị nhỏ nhất của mẫu số thuộc vào nhóm [u₁;u₂) và càng gần u₁ càng tốt. Giá trị lớn nhất của mẫu thuộc nhóm [u_k;u_k+1) và càng gần u_k+1 càng tốt.

⮚ Xét mẫu số liệu ghép nhóm được cho ở bảng sau: (Bảng 1)

Nhóm	[u1;u2)	[u2;u3)	…	[uk;uk+1)
Tần số	n1	n2	…	nk

▪ Giá trị chính giữa của mỗi nhóm được dùng làm giá trị đại diện cho nhóm ấy. Ví dụ nhóm [u₁;u₂) có giá trị đại diện là $\frac{1}{2}\left(u_1+u_2\right)$

▪ Hiệu u_j+1 - u_j được gọi là độ dài của nhóm [u_j; u_j+1)

▪ Số trung bình của mẫu số liệu ghép nhóm:

$\overline{x}=\frac{n_1{c}_1+n_2{c}_2+\mathrm{...}+n_k{c}_k}{n}$, trong đó n = n₁ + n₂ + ... + n_k và c_i là giá trị đại diện của từng nhóm số liệu.

⮚ Mốt

▪ Nhóm chứa mốt của mẫu số liệu ghép nhóm là nhóm có tần số lớn nhất.

▪ Giả sử nhóm chứa mốt là [u_m; u_m+1), khi đó mốt của mẫu số liệu ghép nhóm, kí hiệu là M₀, được xác định bởi công thức

$M_O=u_m+\frac{n_m-n_{m-1}}{\left(n_m-n_{m-1}\right)+\left(n_m-n_{m+1}\right)}\left(u_{m+1}-u_m\right)$

▪ Chú ý: Nếu không có nhóm kể trước của nhóm chứa mốt thì n_m-1 = 0. Nếu không có nhóm kề sau của nhóm chứa mốt thì n_m+1 = 0.

⮚ Trung vị

• Giả sử nhóm [u_m; u_m+1) chứa trung vị;

• n_m là tần số của nhóm chứa trung vị;

• C = n₁ + n₂ + ... + n_m+1

Khi đó: $M_e=u_m+\frac{\frac{n}{2}-C}{n_m}.\left(u_{m+1}-u_m\right)$

B. Các dạng bài tập & phương pháp giải

Dạng 1. Khoảng biến thiên

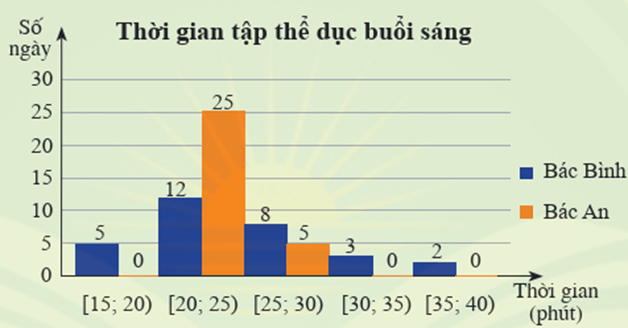
Ví dụ 1. Biểu đồ dưới đây thống kê thời gian tập thể dục buổi sáng mỗi ngày trong tháng 9/2022 của bác Bình và bác An

a) Em hãy chọn số thích hợp thay vào các vị trí được đánh dấu ? ở bảng sau:

Thời gian (phút)	[15; 20)	[20; 25)	[25; 30)	[30; 35)	[35; 40)
Bác Bình	?	12	8	3	2
Bác An	?	?	?	?	?

b) Hãy tìm khoảng biến thiên của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác Bình và bác An.

Ví dụ 2. Bảng sau thống kê cân nặng của 50 quả xoài Thanh Ca được lựa chọn ngẫu nhiên sau khi thu hoạch ở một nông trường.

Cân nặng (g)	[250; 290)	[290; 330)	[330; 370)	[370; 410)	[410; 450)
Số quả xoài	3	13	18	11	5

a) Hãy tìm khoảng biến thiên của mẫu số liệu ghép nhóm trên.

b) Có ý kiến cho rằng: “Trong 50 quả xoài trên, hiệu số cân nặng của hai quả bất kì không vượt quá 200 g”. Ý kiến đó đúng hay sai? Giải thích.

Ví dụ 3. Cô Hà thống kê lại đường kính thân gỗ của một số cây xoan đào 6 năm tuổi được trồng ở một lâm trường ở bảng sau.

Đường kính (cm)	[40; 45)	[45; 50)	[50; 55)	[55; 60)	[60; 65)
Tần số	5	20	18	7	3

Hãy tìm khoảng biến thiên của mẫu số liệu ghép nhóm trên.

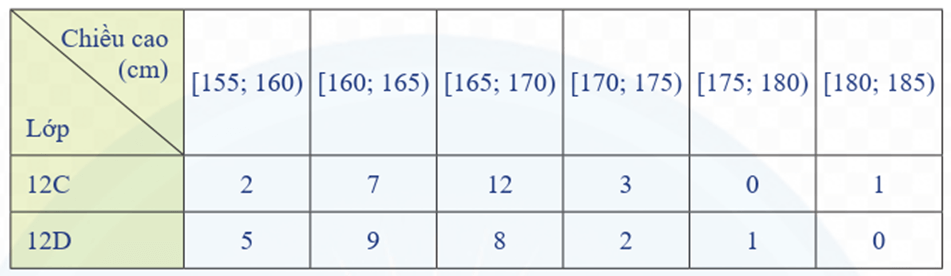
Ví dụ 4. Bạn Trang thống kê lại chiều cao (đơn vị: cm) của các bạn học sinh nữ lớp 12C và lớp 12D ở bảng sau:

Nếu so sánh theo khoảng biến thiên thì chiều cao của học sinh lớp nào có độ phân tán lớn hơn?

Dạng 2. Khoảng tứ phân vị

Ví dụ 5. Hãy tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm trong bảng dưới đây.

Cân nặng (g)	[250; 290)	[290; 330)	[330; 370)	[370; 410)	[410; 450)
Số quả xoài	3	13	18	11	5

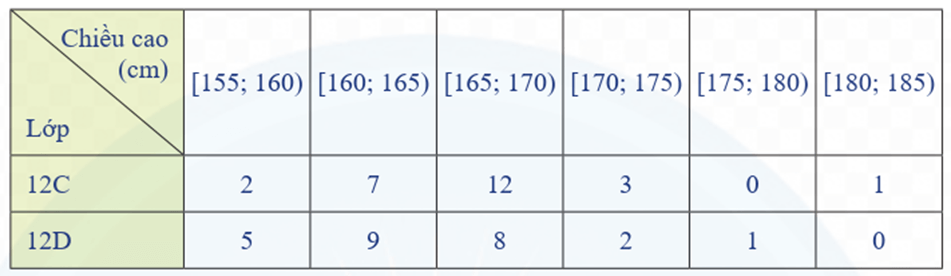
Ví dụ 6. Bạn Trang thống kê lại chiều cao (đơn vị: cm) của các bạn học sinh nữ lớp 12C và lớp 12D ở bảng sau:

Nếu so sánh theo khoảng tứ phân vị thì chiều cao của học sinh lớp nào có độ phân tán lớn hơn?

Ví dụ 7. Hằng ngày ông Thắng đều đi xe buýt từ nhà đến cơ quan. Dưới đây là bảng thống kê thời gian của 100 lần ông Thắng đi xe buýt từ nhà đến cơ quan.

Thời gian (phút)	[15; 18)	[18; 21)	[21; 24)	[24; 27)	[27; 30)	[30; 33)
Số lượt	22	38	27	8	4	1

a) Hãy tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm trên.

b) Biết rằng trong 100 lần đi trên, chỉ có đúng một lần ông Thắng đi hết hơn 29 phút. Thời gian của lần đi đó có phải là giá trị ngoại lệ không?

c) Hãy tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm ở trên sau khi đã loại bỏ các giá trị ngoại lệ. Em có nhận xét gì về khoảng biến thiên, khoảng tứ phân vị vừa tìm được và khoảng biến thiên, khoảng tứ phân vị ban đầu?

................................

................................

................................

Xem thử

Xem thêm Chuyên đề dạy thêm Toán lớp 12 các chủ đề hay khác:

• Chuyên đề Ứng dụng đạo hàm đề khảo sát và vẽ đồ thị hàm số

• Chuyên đề Vectơ và hệ tọa độ trong không gian

• Chuyên đề Nguyên hàm - Tích phân

• Chuyên đề Phương trình mặt phẳng, đường thẳng, mặt cầu

• Chuyên đề Xác suất có điều kiện

---