Xác suất có điều kiện lớp 12 (Chuyên đề dạy thêm Toán 12)

Tài liệu Chuyên đề Xác suất có điều kiện lớp 12 trong Chuyên đề dạy thêm Toán 12 gồm các dạng bài tập từ cơ bản đến nâng cao với phương pháp giải chi tiết và bài tập tự luyện đa dạng giúp Giáo viên có thêm tài liệu giảng dạy Toán 12.

Xác suất có điều kiện lớp 12 (Chuyên đề dạy thêm Toán 12)

Xem thử

Chỉ từ 400k mua trọn bộ Chuyên đề dạy thêm Toán 12 (sách mới) bản word có lời giải chi tiết:

• B1: gửi phí vào tk: 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án

A. Kiến thức cần nhớ

1. Định nghĩa

• Cho hai biến cố A và B. Xác suất của biến cố A với điều kiện biến cố B đã xảy ra được gọi là xác suất của A với điều kiện B, kí hiệu là P(A|B).

Nếu P(B) > 0 thì $\text{P}(A\mid B)=\frac{\text{P}\left(AB\right)}{\text{P}\left(B\right)}$

2. Nhận xét

• Từ định nghĩa của xác suất có điều kiện, ta suy ra:

Nếu P(B) > 0 thì P(AB) = P(B).P(A|B)

• Người ta chứng minh được rằng: Nếu A, B là hai biến cố bất kì thì

P(AB) = P(A).P(B|A) = P(AB) = P(B).P(A|B) (Công thức nhân xác suất.)

• Cho hai biến cố A và B với P(B) > 0. Khi đó, ta có:

$\text{P}(A\mid B)=\frac{n\left(AB\right)}{n\left(B\right)}\text{.}$

• Cho A và B là hai biến cố với 0 < P(A) < 1,0 < P(B) < 1. Khi đó, A và B là hai biến cố độc lập khi và chỉ khi

P(A) = P(A|B) = $P\left(A\right|\overline{B})$ và P(B) = P(B|A) = $P\left(B\right|\overline{A})$

B. Các dạng bài tập & phương pháp giải

Dạng 1. Tính xác suất có điều kiện bằng công thức

Ví dụ 1. Bạn Thủy gieo một con xúc xắc cân đối và đồng chất. Nếu biết rằng xuất hiện mặt chẵn chấm thì xác suất xuất hiện mặt 6 chấm là bao nhiêu?

Ví dụ 2. Hoạt động khám phá 1 trang 69 Toán 12 Tập 2: Hộp thứ nhất chứa 2 viên bi xanh và 1 viên bi đỏ. Hộp thứ hai chứa 2 viên bi xanh và 3 viên bi đỏ. Các viên bi có cùng kích thước và khối lượng. Bạn Thanh lấy ra ngẫu nhiên 1 viên bi từ hộp thứ nhất bỏ vào hộp thứ hai, sau đó lại lấy ra ngẫu nhiên 1 viên bi từ hộp thứ hai. Gọi A là biến cố "Viên bi lấy ra lần thứ nhất là bi xanh"; B là biến cố "Viên bi lấy ra lần thứ hai là bi đỏ".

a) Biết rằng biến cố A xảy ra, tính xác suất của biến cố B .

b) Biết rằng biến cố A không xảy ra, tính xác suất của biến cố B .

Ví dụ 3. Một hộp chứa ba tấm thẻ cùng loại được ghi số lần lượt từ 1 đến 3 . Bạn Hà lấy ra một cách ngẫu nhiên một thė từ hộp, bỏ thè đó ra ngoài và lại lấy ra một cách ngẫu nhiên thêm một thẻ nữa. Xét các biến cố:

A: "Thẻ lấy ra lần thứ nhất ghi số 1 ";

B: "Thẻ lấy ra lần thứ nhất ghi số 2 ";

C: "Thẻ lấy ra lần thứ hai ghi số lè".

a) Xác định không gian mẫu của phép thử. Viết tập hợp các kết quả thuận lợi cho mỗi biến cố A, B, C.

b) Tính xác suất để thẻ lấy ra lần thứ hai ghi số lè, biết rằng thẻ lấy ra lần thứ nhất ghi số 1 .

c) Tính xác suất để thẻ lấy ra lần thứ hai ghi số lè, biết rằng thẻ lấy ra lần thứ nhất ghi số 2 .

d) Gọi D là biến cố "Thẻ lấy ra lần thứ hai ghi số lớn hơn 1". Tính P(D|A) và P(D|B)

Ví dụ 4. Câu lạc bộ cờ của nhà trường gồm 35 thành viên, mỗi thành viên biết chơi ít nhất một trong hai môn cờ vua hoặc cờ tướng. Biết rằng có 25 thành viên biết chơi cờ vua và 20 thành viên biết chơi cờ tướng. Chọn ngẫu nhiên 1 thành viên của câu lạc bộ.

a) Tính xác suất thành viên được chọn biết chơi cờ vua, biết rằng thành viên đó biết chơi cờ tướng.

b) Tính xác suất thành viên được chọn không biết chơi cờ tướng, biết rằng thành viên đó biết chơi cờ vua.

Ví dụ 5. Hoạt động khám phá 2 trang 70 Toán 12 Tập 2: Gieo đồng thời hai con xúc xắc cân đối và đồng chất. Gọi A là biến cố "Xuất hiện hai mặt có cùng số chấm", B là biến cố "Tổng số chấm của hai mặt xuất hiện bằng 8 " và C là biến cố "Xuất hiện ít nhất một mặt có 6 chấm".

a) Tính $\frac{P(A\cap B)}{P\left(B\right)}$ và P(A|B)

b) Tính $\frac{P(C\cap A)}{P\left(A\right)}$ và P(C|A)

Ví dụ 6. Một công ty bảo hiểm nhận thấy có 48% số người mua bảo hiểm ô tô là phụ nữ và có 36% số người mua bảo hiểm ô tô là phụ nữ trên 45 tuổi.

a) Biết một người mua bảo hiểm ô tô là phụ nữ, tính xác suất người đó trên 45 tuổi.

b) Tính tỉ lệ người trên 45 tuổi trong số những người phụ nữ mua bảo hiểm ô tô.

Ví dụ 7. Ví dụ 4. Cho hai biến cố A và B có P(A) = 0, 3; P(B) = 0,5 và P(A|B) = 0,4. Tính $P\left(\overline{A}B\right)$ và $P(\overline{A}\mid B)$

Ví dụ 8. Một nhóm 5 học sinh nam và 4 học sinh nữ tham gia lao động trên sân trường. Cô giáo chọn ngẫu nhiên đồng thời 2 bạn trong nhóm đi tưới cây. Tính xác suất để hai bạn được chọn có cùng giới tính, biết rằng có ít nhất 1 bạn nam được chọn.

Ví dụ 9. Kết quả khảo sát những bệnh nhân bị tai nạn xe máy về mối liên hệ giữa việc đội mũ bảo hiểm và khả năng bị chấn thương vùng đầu cho thấy:

- Tỉ lệ bệnh nhân bị chấn thương vùng đầu khi gặp tai nạn là 80%;

- Tỉ lệ bệnh nhân đội mũ bảo hiểm đúng cách khi gặp tai nạn là 90%;

- Tỉ lệ bệnh nhân đội mũ bảo hiểm đúng cách bị chấn thương vùng đầu là 18%.

Hỏi theo kết quả điều tra trên, việc đội mũ bảo hiểm đúng cách sẽ làm giảm khả năng bị chấn thương vùng đầu bao nhiêu lần?

Dạng 2. Tính xác suất có điều kiện bằng sơ đồ hình cây

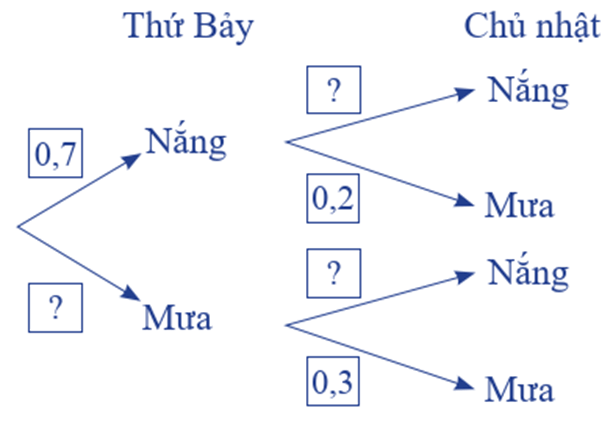
Ví dụ 10. Bạn Việt chuẩn bị đi tham quan một hòn đảo trong hai ngày thứ Bảy và Chủ nhật. Ở hòn đảo đó, mỗi ngày chỉ có nắng hoặc mưa, nếu một ngày là nắng thì khả năng xảy ra mưa ở ngày tiếp theo là 20%, còn nếu một ngày là mưa thì khả năng ngày hôm sau vẫn mưa là 30%. Theo dự báo thời tiết, xác suất trời sẽ nắng vào thứ Bảy là 0,7 .

Hãy tìm các giá trị thích hợp thay vào ô có dấu ? ở sơ đồ hình cây sau:

Ví dụ 11. Ở một sân bay, người ta sử dụng một loại máy soi tự động phát hiện hàng cấm trong hành lí kí gửi. Máy phát chuông cảnh báo với 95% các kiện hành lí có chứa hàng cấm và 2% các kiện hành lí không chứa hàng cấm. Tỉ lệ các kiện hành lí có chứa hàng cấm là 0,1%.

Chọn ngẫu nhiên một kiện hành lí để soi bằng máy trên. Sử dụng sơ đồ hình cây, tính xác suất của các biến cố:

M: "Kiện hành lí có chứa hàng cấm và máy phát chuông cảnh báo";

N: "Kiện hành lí không chứa hàng cấm và máy phát chuông cảnh báo".

Ví dụ 12. Hộp thứ nhất có 4 viên bi xanh và 6 viên bi đỏ. Hộp thứ hai có 5 viên bi xanh và 4 viên bi đỏ. Các viên bi có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên 1 viên bi từ hộp thứ nhất chuyển sang hộp thứ hai. Sau đó lại lấy ra ngẫu nhiên 1 viên bi từ hộp thứ hai.

Sử dụng sơ đồ hình cây, tính xác suất của các biến cố:

A: "Viên bi lấy ra từ hộp thứ nhất có màu xanh và viên bi lấy ra từ hộp thứ hai có màu đỏ";

B: "Hai viên bi lấy ra có cùng màu".

Ví dụ 13. Một trường đại học tiến hành khảo sát tình trạng việc làm sau khi tốt nghiệp của sinh viên. Kết quả khảo sát cho thấy tỉ lệ người tìm được việc làm đúng chuyên ngành là 70% đối với sinh viên tốt nghiệp loại giỏi và 30% đối với sinh viên tốt nghiệp loại khác.

Tỉ lệ sinh viên tốt nghiệp loại giỏi là 30%. Gặp ngẫu nhiên một sinh viên đã tốt nghiệp của trường.

Sử dụng sơ đồ hình cây, tính xác suất của các biến cố:

C: "Sinh viên tốt nghiệp loại giỏi và tìm được việc làm đúng chuyên ngành";

D : "Sinh viên không tốt nghiệp loại giỏi và tìm được việc làm đúng chuyên ngành".

C. Bài tập tự luận rèn luyện

Dạng 1. Tính xác suất có điều kiện bằng công thức

Câu 1. Cho hai biến cố A và B có P(A) = 0,4; P(B) = 0,8 và $P(A\mid \overline{B})=0,5$. Tính $P\left(A\overline{B}\right)$ và P(A|B)

Câu 2. Cho hai biến cố A, B có P(A) = 0,5; P(B) = 0,8; P(A∩B) = 0,4.. Tính các xác suất sau: P(A|B), P(B|A)

Câu 3. Cho P(A) = 0,2; P(B) = 0,51; P(B|A) = 0,8. Tính P(A|B).

Câu 4. Cho hai biến cố A, B có P(A) = 0,4; P(B) = 0,6; P(A∩B) = 0,2. Tính các xác suất sau: P(A|B), P(B|A)

Câu 5. Cho hai biến cố độc lập A, B với P(A) = 0,8; P(B) = 0,25. Tính P(A|B).

Câu 6. Cho hai biến cố A, B có P(A) = 0,6; P(B) = 0,8; P(A∩B) = 0,4. Tính các xác suất sau:

a) P(B|A)

b) $\text{P}(A\cap \overline{B})$

c) $\text{P}(\overline{B}\mid A)$

Câu 7. Nếu hai biến cố A, B thoả mãn P(B) = 0,6; P(A∩B) = 0,2 thì P(A|B) bằng bao nhiêu?

Câu 8. Nếu hai biến cố A, B thoả mãn P(B) = 0,3; P(A|B) = 0,5 thì P(A∩B) bằng bao nhiêu?

Câu 9. Cho hai biến cố ngẫu nhiên A và B. Biết rằng P(A|B) = 2P(B|A) và P(AB) ≠ 0. Tính tỉ số $\frac{P\left(A\right)}{P\left(B\right)}$

Câu 10. Trong một hộp kín có 7 chiếc bút bi xanh và 5 chiếc bút bi đen, các chiếc bút có cưng kích thước và khối lượng. Bạn Sơn lấy ngẫu nhiên một chiếc bút bi trong hộp, không trả lại. Sau đó Tùng lấy ngẫu nhiên một trong 11 chiếc bút còn lại. Tính xác suất để Tùng lấy được bút bi xanh nếu biết ră̆ng Sơn đã lấy được bút bi đen.

Câu 11. Một thư viện có 35% tồng số sách là sách khoa học, 14% tổng số sách là sách khoa học tự nhiên. Chọn ngẫu nhiên một quyển sách của thư viện. Tính xác suất để quyển sách được chọn là sách khoa học tự nhiên, biết rằng đó là quyền sách về khoa học.

Câu 12. Một khu dân cư có 85% các hộ gia đình sử dụng điện để đun nước. Hơn nữa, có 21% các hộ gia đình sử dụng ấm điện siêu tốc. Chọn ngẫu nhiên một hộ gia đình, tính xác suất hộ đó sử dụng ấm điện siêu tốc, biết hộ đó sử dụng điện để đun nước.

................................

................................

................................

Xem thử

Xem thêm Chuyên đề dạy thêm Toán lớp 12 các chủ đề hay khác:

• Chuyên đề Ứng dụng đạo hàm đề khảo sát và vẽ đồ thị hàm số

• Chuyên đề Vectơ và hệ tọa độ trong không gian

• Chuyên đề Các số đặc trưng đo mức độ phân tán của mẫu số liệu ghép nhóm

• Chuyên đề Nguyên hàm - Tích phân

• Chuyên đề Phương trình mặt phẳng, đường thẳng, mặt cầu

---