Chuyên đề dạy thêm Toán 8 năm 2026 (có lời giải)
Tài liệu chuyên đề dạy thêm Toán 8 gồm các dạng bài tập từ cơ bản đến nâng cao với phương pháp giải chi tiết và bài tập tự luyện đa dạng giúp Giáo viên có thêm tài liệu giảng dạy Toán 8.
Chuyên đề dạy thêm Toán 8 năm 2026 (có lời giải)
(199k) Xem Khóa học Toán 8 KNTTXem Khóa học Toán 8 CTSTXem Khóa học Toán 8 CD
Chỉ từ 500k mua trọn bộ (Chuyên đề) Phương pháp giải Toán 8 (cơ bản, nâng cao) bản word có lời giải chi tiết:
- B1: gửi phí vào tk:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án
Chuyên đề dạy thêm Toán 8 Kết nối tri thức
Chuyên đề dạy thêm Toán 8 Chân trời sáng tạo
Chuyên đề dạy thêm Toán 8 Cánh diều
Chuyên đề Đa thức lớp 8
Chủ đề 1: ĐƠN THỨC
Dạng 1: ĐƠN THỨC VÀ ĐƠN THỨC THU GỌN
A. PHƯƠNG PHÁP
1. Đơn thức là biểu thức đại số chỉ gồm một số, hoặc một biển, hoặc một tích các số và các biến.
Số 0 được gọi là đơn thức 0.
2. Đơn thức thu gọn là đơn thức chỉ gồm tích của một số với các biến. Mà mỗi biến được nâng lên lũy thừa với số mũ nguyên dương.
Số nói trên là hệ số, phần còn lại gọi là phần biến của đơn thức thu gọn.
3. Bậc của đơn thức có hệ số khác 0 là tổng số mũ của tất cả các biến có trong đơn thức đó.
Số thực khác 0 là đơn thức có bậc bằng 0, số 0 được coi là đơn thức không có bậc.
4. Để nhân hai hai nhiều đơn thức. Ta nhân các hệ số với nhau và nhân các phần biến với nhau.
5. Hai đơn thức đồng dạng là hai đơn thức có hệ số khác 0 và có cùng phần biến. Các số khác 0 được coi là những đơn thức đồng dạng.
6. Để cộng (hay trừ) các đơn thức đồng dạng, ta cộng (hay trừ) các hệ số với nhau và giữ nguyên phần biến.
* Cách xác định đơn thức, bậc của đơn thức.
+ Một biểu thức đại số là đơn thức nếu là một số, một biến hoặc tích của các số và
các biến.
+ Để Xác định phần biến, phần hằng của đơn thức và bậc của nó. Trước hết ta phải thu gọn đơn thức về dạng tích của một số với cách biến mà mỗi biến được nâng lên lũy thừa số mũ nguyên dương. Hệ số là phần hằng, phần còn lại là phần biến. Tổng số mũ của tất cả các biến là bậc của đơn thức.
Chẳng hạn:
+ \[A = 2023{x^2}{y^3}{z^4}\]có hệ số là 2023, phần biến là \[{x^2}{y^3}{z^4}\]và có bậc là: \[2 + 3 + 4 = 9\]
B. BÀI TẬP MẪU CÓ HƯỚNG DẪN GIẢI
Bài tập mẫu 1: Trong các biểu thức sau, biểu thức nào là đơn thức:
Hướng dẫn giải
Các biểu thức là đơn thức là: \[\frac{1}{2}x3{y^4}{z^5};\frac{{3{x^2}}}{{4{b^3}}}; - 2024\].
Các biểu thức là đơn thức là: \[\frac{1}{2} + {x^3}{y^4}{z^5};\frac{{4{x^2}}}{{3{y^3}}};\frac{{\left( {3x + y} \right)x{y^2}}}{a}\]
Bài tập mẫu 2: Thu gọn đơn thức và tìm bậc của nó: \[{x^2}.2{y^3}3xyz\].
Hướng dẫn giải
+ Thu gọn là: \[6{x^3}{y^4}z.\]
+ Bậc của đơn thức: \[3 + 4 + 1 = 8\]
Bài tập mẫu 3: Thu gọn đơn thức và chỉ ra phần hệ số, phần biến và bậc của các đơn thức thu gọn đó:
a. \(\left( {\frac{3}{5}{x^3}{y^4}} \right)\left( {\frac{{10}}{9}{x^4}{y^2}} \right)\);
b. \(\left( {\frac{5}{7}{x^3}{y^4}} \right)\left( {\frac{2}{3}{x^4}{y^2}} \right)\left( {\frac{{ - 7}}{{10}}x{y^3}} \right)\)
Hướng dẫn giải
a. Thu gọn đơn thức: \(\left( {\frac{3}{5}{x^3}{y^4}} \right)\left( {\frac{{10}}{9}{x^4}{y^2}} \right)\)\[ = \frac{2}{3}{x^7}{y^6}\]
+ Hệ số của đơn thức: \[\frac{2}{3}\].
+ Phần biến của đơn thức: \[{x^7}{y^6}\]
+ Bậc đơn thức: \[7 + 6 = 13\]
b. Thu gọn đơn thức: \[\frac{5}{7}.\frac{2}{3}.\frac{{ - 7}}{{10}}{x^3}{x^4}x{y^4}{y^2}{y^3} = \frac{{ - 1}}{3}{x^{3 + 4 + 1}}{y^{4 = 2 + 3}} = \frac{{ - 1}}{3}{x^8}{y^9}.\]
+ Hệ số của đơn thức: \[\frac{{ - 1}}{3}\]
+ Phần biến của đơn thức: \[{x^8}{y^9}\]
+ Bậc đơn thức: \[8 = 9 = 17\]
Bài tập mẫu 4: Thu gọn các đơn thức sau :
a.\[\frac{1}{4}{x^2}{y^2}\]. \(\frac{4}{3}x{y^3}\)
b. \(\left( { - 2{x^3}y} \right).x{y^2}.\frac{1}{2}{y^5}\).
Hướng dẫn giải
Thu gọn: a. \[\frac{1}{4}{x^2}{y^2}.\frac{4}{3}x{y^3} = \frac{1}{3}{x^3}{y^5}\]
b. \[\left( { - 2{x^3}y} \right).x{y^2}.\frac{1}{2}{y^5} = - {x^4}{y^8}\]
Bài tập mẫu 5: Thu gọn các đơn thức sau rồi cho biết hệ số, phần biến và bậc của chúng.
a. \[\left( { - \frac{1}{3}{x^2}yz} \right)\left[ {\frac{1}{7}{{\left( {xy} \right)}^4}} \right]\left( {\frac{7}{9}xy{z^3}} \right) = - \frac{1}{{27}}{x^7}{y^6}{z^4}\](a là hằng số).
b. \[\frac{1}{2}x{y^4}{z^3}{\left( { - \frac{1}{5}{x^2}y} \right)^2}{\left( { - z} \right)^5}\].
Hướng dẫn giải
a. Ta có: \[\left[ { - \frac{1}{5}\left( { - 5} \right).a} \right]\left( {{x^2}{x^3}x} \right)\left( {{y^3}.y} \right) = a{x^6}{y^4}\]
Vậy đơn thức có hệ số bằng a, phần biến là \[{x^6}{y^4}\], bậc là 10.
b. Ta có: \[\left( { - \frac{1}{2}} \right)\left( {\frac{1}{{25}}} \right)x{y^4}{z^3}.{x^4}{y^2}.{z^5} = - \frac{1}{{50}}{x^5}{y^6}{z^8}\]
Đơn thức: \[ - \frac{1}{{50}}{x^5}{y^6}{z^8}\], có phần hệ số là \[ - \frac{1}{{50}}\], phần biến là \[{x^5}{y^6}{z^8}\] và có bậc là 19.
C. BÀI TẬP LUYỆN TẬP
Bài tập 1: Trong các biểu thức sau, biểu thức nào là đơn ? Biểu thức nào là đơn thức thu gọn.
\[ - 5x{y^2}\]; \[xyz + xz\];
\[2\left( {{x^2} + {y^2}} \right)\];
\[ - 3x4yxz\].
Bài tập 2: Cho biết phần hệ số, phần biến và bậc của mỗi đơn thức sau.
a. \[{\left( {4{x^2}} \right)^2}\left( { - 5{y^3}} \right){\left( { - xy} \right)^2}\]
b. \[\left( { - {x^2}y} \right){\left( { - \frac{1}{2}axz} \right)^2}{\left( {xyz} \right)^3}\] (a là hằng số)
................................
................................
................................
Trên đây tóm tắt một số nội dung miễn phí có trong bộ Chuyên đề dạy thêm Toán 8 mới nhất, để mua tài liệu đầy đủ, Thầy/Cô vui lòng xem thử:
(199k) Xem Khóa học Toán 8 KNTTXem Khóa học Toán 8 CTSTXem Khóa học Toán 8 CD
Xem thêm giáo án, đề thi lớp 8 các môn học hay khác:
Xem thêm các loạt bài Để học tốt Toán lớp 8 hay khác:
Tủ sách VIETJACK shopee lớp 6-8 (2025):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Loạt bài Lý thuyết & 700 Bài tập Toán lớp 8 có lời giải chi tiết có đầy đủ Lý thuyết và các dạng bài có lời giải chi tiết được biên soạn bám sát nội dung chương trình sgk Đại số 8 và Hình học 8.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 8 Global Success
- Giải sgk Tiếng Anh 8 Smart World
- Giải sgk Tiếng Anh 8 Friends plus
- Lớp 8 - Kết nối tri thức
- Soạn văn 8 (hay nhất) - KNTT
- Soạn văn 8 (ngắn nhất) KNTT
- Giải sgk Toán 8 - KNTT
- Giải sgk Khoa học tự nhiên 8 - KNTT
- Giải sgk Lịch Sử 8 - KNTT
- Giải sgk Địa Lí 8 - KNTT
- Giải sgk Giáo dục công dân 8 - KNTT
- Giải sgk Tin học 8 - KNTT
- Giải sgk Công nghệ 8 - KNTT
- Giải sgk Hoạt động trải nghiệm 8 - KNTT
- Giải sgk Âm nhạc 8 - KNTT
- Lớp 8 - Chân trời sáng tạo
- Soạn văn 8 (hay nhất) - CTST
- Soạn văn 8 (ngắn nhất) - CTST
- Giải sgk Toán 8 - CTST
- Giải sgk Khoa học tự nhiên 8 - CTST
- Giải sgk Lịch Sử 8 - CTST
- Giải sgk Địa Lí 8 - CTST
- Giải sgk Giáo dục công dân 8 - CTST
- Giải sgk Tin học 8 - CTST
- Giải sgk Công nghệ 8 - CTST
- Giải sgk Hoạt động trải nghiệm 8 - CTST
- Giải sgk Âm nhạc 8 - CTST
- Lớp 8 - Cánh diều
- Soạn văn 8 Cánh diều (hay nhất)
- Soạn văn 8 Cánh diều (ngắn nhất)
- Giải sgk Toán 8 - Cánh diều
- Giải sgk Khoa học tự nhiên 8 - Cánh diều
- Giải sgk Lịch Sử 8 - Cánh diều
- Giải sgk Địa Lí 8 - Cánh diều
- Giải sgk Giáo dục công dân 8 - Cánh diều
- Giải sgk Tin học 8 - Cánh diều
- Giải sgk Công nghệ 8 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 8 - Cánh diều
- Giải sgk Âm nhạc 8 - Cánh diều

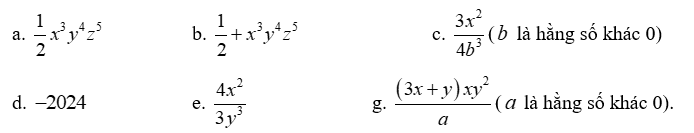



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

