Bài toán thực tế liên quan đến bất đẳng thức lớp 9 (cách giải + bài tập)

Chuyên đề phương pháp giải bài tập Một số bài toán thực tế liên quan đến bất đẳng thức lớp 9 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Một số bài toán thực tế liên quan đến bất đẳng thức.

Bài toán thực tế liên quan đến bất đẳng thức lớp 9 (cách giải + bài tập)

1. Phương pháp giải

• Các bước giải bài toán thực tế liên quan đến bất đẳng thức

Bước 1. Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số.

Bước 2. Dựa vào dữ kiện bài toán để tìm ẩn số.

Bước 3. Kiểm tra xem trong các nghiệm vừa tìm được có thỏa mãn điều kiện của ẩn hay không rồi kết luận.

2. Ví dụ minh họa

Ví dụ 1. Một ca nô di xuôi dòng trong 2 giờ 30 phút. Biết rằng tốc độ của ca nô khi nước yên lặng không quá 40 km/h và tốc độc của dòng nước là 6 km/h. Chứng minh quãng đường ca nô đi được trong thời gian trên không vượt quá 115 km/h.

Hướng dẫn giải

Gọi tốc dộ của ca nô khi nước yên lặng là x (x > 6, km/h).

Tốc độ ca nô đi xuôi dòng là x + 6 (km/h).

Ta có x ≤ 40 nên x + 4 ≤ 40 + 6 hay x + 6 ≤ 46.

Gọi s (km) là quãng đường ca nô đi được trong 2 giờ 30 phút (= 2,5 giờ).

Ta có: s = 2,5(x + 6) (km).

Do x + 6 ≤ 46 nên 2,5(x + 6) ≤ 2,5.46 = 115 hay s ≤ 115.

Vậy quãng đường ca nô đi được trong 2 giờ 30 phút không vượt quá 115 km.

Ví dụ 2. Một nhà tài trợ dự kiến tổ chức một buổi đi dã ngoại tập thể nhằm giúp các bạn học sinh vùng cao trải nghiệm thực tế tại một trang trại trong 1 ngày (từ 14h ngày hôm trước đến 12h ngày hôm sau). Cho biết số tiền tài trợ dự kiến là 30 triệu đồng và giá thuê các dịch vụ và phòng nghỉ trưa là 17 triệu đồng 1 ngày, giá mỗi suất ăn trưa, ăn tối là 60 nghìn đồng và mỗi suất ăn sáng là 30 nghìn đồng. Hỏi có thể tổ chức nhiều nhất cho bao nhiêu bạn tham gia được?

Hướng dẫn giải

Gọi số bạn tham gia là x (x ∈ ℕ^*).

Theo đề bài, ta có:

17 000 000 + (60 000 + 30 000)x ≤ 30 000 000 hay 90 000x ≤ 13 000 000.

Suy ra x ≤ $\frac{1300}{9}$ = 144,4444….

Vậy có thể tổ chức nhiều nhất cho 144 bạn tham gia.

3. Bài tập tự luyện

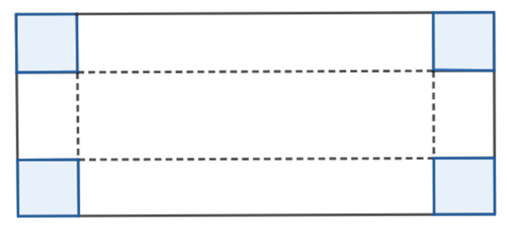
Bài 1. Một tấm bìa cứng hình chữ nhật có chiều dài là 50 cm và chiều rộng là 30 cm. Bạn Linh cắt ở mỗi góc một tấm bìa hình vuông cạnh x (cm) và xếp phần còn lại thành một hình hộp không nắp. Tìm x để diện tích xung quanh của hình hộp chữ nhật sau khi cắt là lớn nhất.

A. x = 800.

B. x = 100.

C. x = 10.

D. x = 8.

Hướng dẫn giải

Đáp án đúng là: C

Diện tích tấm bìa hình chữ nhật này là: 50.30 = 1500 (cm²).

Chiều dài sau khi cắt tấm bìa là: 50 – 2x (cm).

Chiều rộng sau khi cắt tấm bìa là: 30 – 2x (cm).

Diện tích xung quanh của hộp là:

2x (50 – 2x + 30 – 2x) = 2x(80 – 4x) = −8x² + 160x (cm²).

Diện tích xung quanh của hình hộp chữ nhật sau khi cắt là lớn nhất thì

−8x² + 160x đạt giá trị lớn nhất.

Ta có: −8x² + 160x = −8(x² – 20x + 100) + 800 = −8(x – 10)² + 800.

Nhận thấy −8(x – 10)² ≤ 0 nên −8(x – 10)² + 800 ≤ 800.

Dấu “=” xảy ra khi x – 10 = 0 hay x = 10.

Vậy diện tích xung quanh hình hộp chữ nhật là 800 cm² khi x = 10 cm.

Bài 2. Một cửa hàng chuyên kinh doanh máy tính tại Hà Nội. Một loại máy tính có giá nhập vào một chiếc là 18 triệu đồng và bán ra với giá 22 triệu đồng. Với giá bán như trên thì một năm số lượng máy tính bán được dự kiến 500 chiếc. Để tăng thêm lượng tiêu thụ dòng máy tính này, chủ cửa hàng dự định giảm giá bán và ước lượng cứ giảm 200 nghìn một chiếc thì số lượng máy tính bán ra trong năm sẽ tăng 50 chiếc. Vậy cửa hàng phải bán với giá bao nhiêu để sau khi giảm giá lợi nhuận thu được sẽ cao nhất?

A. 21 triệu đồng.

B. 17 triệu đồng.

C. 19 triệu đồng.

D. 20 triệu đồng.

Hướng dẫn giải

Đáp án đúng là: A

Gọi x là giá mà cửa hàng phải bán để sau khi giảm giá thu được lợi nhuận cao nhất (x > 0, triệu đồng).

Theo đề, số tiền mà của hàng sẽ giảm là 22 – x (triệu đồng) mỗi chiếc.

Khi đó, số lượng máy tính tăng lên là: 50(22 – x) : 0,2 = 250(22 – x) chiếc.

Do đó, số lượng máy tính mà doanh nghiệp bán được là:

500 + 250(22 – x) = 6000 – 250x (chiếc)

Doanh thu mà cửa hàng sẽ đạt được là: (6000 – 250x)x (triệu đồng).

Tiền mà cửa hàng bỏ ra để nhập máy tính sẽ là:

18(6000 – 250x) = 108000 – 4500x (triệu đồng)

Lợi nhuận mà cửa hàng thu được sau khi bán giá mới là:

(6000 – 250x)x – 108000 + 4500x = −250x² + 10500x – 108000 (triệu đồng).

Ta có: −250x² + 10500x – 108000 = −250(x – 21)² + 2250 ≤ 2250.

Dấu “=” xảy ra khi −250(x – 21)² = 0 suy ra x – 21 = 0 khi x = 21.

Vậy cửa hàng bán với giá 21 triệu đồng thì doanh thu nhận được là lớn nhất.

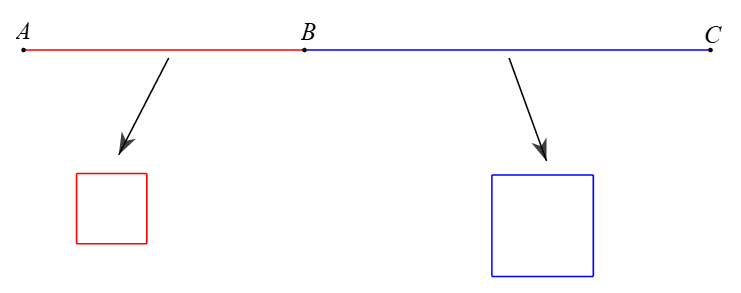
Bài 3. Một sợi dây thép AC có chiều dài 8 m được chia thành hai phần AB, AC (như hình vẽ minh họa dưới đây).

Mỗi phần đều được uốn thành một hình vuông. Hỏi phải chia sợi dây ban đầu như thế nào để tổng diện tích hai hình vuông thu được sau khi uốn là nhỏ nhất?

A. AB = BC = 4 m.

B. AB = 2 m, BC = 6 m.

C. AB = 3 m, BC = 5 m.

D. AB = 5 m, BC = 4 m.

Hướng dẫn giải

Đáp án đúng là: A

Gọi cạnh hình vuông được uốn từ đoạn AB là x (0 < x < 8, m).

Lúc này, độ dài đoạn AB chính là chu vi hình vuông đó và bằng 4x (m).

Do đó, độ dài đoạn BC là 8 – 4x (m).

Suy ra độ dài cạnh hình vuông được uốn bởi đoạn BC là $\frac{8-4x}{4}$ = 2 – x (m).

Tổng diện tích hai hình vuông lúc này là x² + (2 – x)² (m²).

Ta có: x² + (2 – x)² = 2x² – 4x + 4 = 2(x² – 2x + 1) + 2 = 2(x – 1)² + 2 ≥ 2.

Tổng diện tích hai hình vuông đạt giá trị nhỏ nhất bằng 2 m² khi x – 1 = 0 hay

x = 1.

Khi đó, độ dài đoạn thẳng AB = 4 m và độ dài đoạn thẳng BC = 8 – 4 = 4 m hay B là trung điểm của đoạn AC.

Vậy để tổng diện tích hai hình vuông đạt giá trị lớn nhất thì ta chia đoạn dây thép thành hai phần bằng nhau AB = BC = 4 m.

Bài 4. Xưa kia có một vị tể tướng nổi tiếng thông thái. Đến khi tể tướng muốn cáo quan về quê, nhà vua liền ban thưởng bằng cách đưa cho tể tướng một đoạn dây dài 300 mét và nói: “Ngươi hãy căng sợi dây này thành một hình chữ nhật, sao cho hai đầu dây chạm vào nhau. Khi đó, mảnh đất hình chữ nhật sẽ thuộc về ngươi”. Hỏi tể tướng sẽ căng sợi dây như thế nào để mảnh đất có diện tích lớn nhất?

A. Căng thành hình vuông với độ dài cạnh là 75 m.

B. Căng thành hình vuông với độ dài cạnh là 50 m.

C. Căng thành hình vuông với độ dài cạnh là 100 m.

D. Căng thành hình vuông với độ dài cạnh là 25 m.

Hướng dẫn giải

Đáp án đúng là: A

• Gọi kích thước hình chữ nhật mà tể tướng sẽ căng là x và y (0 < x, y < 150).

Khi đó, ta có chu vi mảnh đất hình chữ nhật đó là 300 m,

suy ra x + y = 300 : 2 = 150 (m).

Diện tích của mảnh đất là S = xy (m²).

• Chứng minh bổ đề: $\frac{{\left(x+y\right)}^2}{4}\ge xy$ với mọi x, y > 0.

Thật vậy, với mọi x, y > 0, ta có:

(x – y)² ≥ 0

x² – 2xy + y² ≥ 0

(x + y)² – 4xy ≥ 0

$\frac{{\left(x+y\right)}^2}{4}\ge xy$.

Đẳng thức xảy ra khi x = y.

Áp dụng bất đẳng thức trên, ta có: $S=xy\le \frac{{\left(x+y\right)}^2}{4}$

Suy ra S ≤ $\frac{{150}^2}{4}$ = 5 625.

Dấu “=” xảy ra khi x = y = $\frac{150}{4}$ = 75 m.

Vậy tể tướng đó cần căng sợi dây bao quanh mảnh đất hình vuông có cạnh 75 m để mảnh đất nhận được có diện tích lớn nhất.

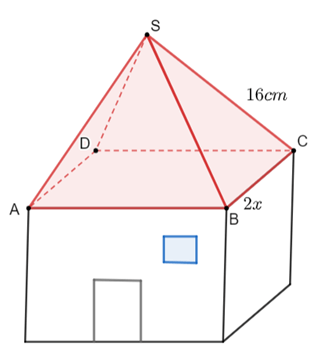
Bài 5. Bạn Nam làm một căn nhà đồ chơi bằng gỗ có phần mái là một chóp tứ giác đều. Biết các cạnh bên của mái nhà bạn Nam dùng các thanh gỗ có chiều dài 16 cm. Bạn Nam dự định dùng giấy màu để phủ kín phần mái nhà. Gọi độ dài cạnh đáy của phần mái là 2x (cm). Hỏi diện tích giấy màu cần sử dụng nhiều nhất là bao nhiêu?

A. 512 cm².

B. 256 cm².

C. 128 cm².

D. 1048 cm².

Hướng dẫn giải

Đáp án đúng là: A

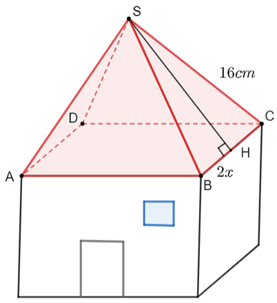
Diện tích giấy màu cần sử dụng chỉnh bằng tổng diện tích bốn mặt bên là các tam giác cân có cạnh bên bằng 16 cm và cạnh đáy bằng 2x cm.

Xét tam giác SBC, kẻ đường cao SH vuông với BC tại H.

Do tam giác SBC cân tại S nên SH vừa là đường cao, vừa là đường trung trực.

Suy ra H là trung điểm của BC.

Suy ra BH = HC = $\frac{BC}{2}$ = x cm (0 < x < 16).

Áp dụng định li Pythagore vào tam giác SHC, ta có:

SH² + HC² = SC²

SH² = 16² – x²

SH² = 256 – x²

SH =$\sqrt{256-x^2}$

Diện tích tam giác SBC là $\frac{1}{2}.2x.\sqrt{256-x^2}=x\sqrt{256-x^2}$(cm²).

Diện tích giấy màu cần sử dụng là 4$x\sqrt{256-x^2}$(cm²).

Thực hiện tính giá trị lớn nhất của S = 4$x\sqrt{256-x^2}$ với 0 < x < 16.

Ta có: $4x\sqrt{256-x^2}=4\sqrt{256x^2-x^4}$

$=4\sqrt{-\left(x^4-2.128x^2+{128}^2\right)+{128}^2}$

$=4\sqrt{-{\left(x^2-128\right)}^2+{128}^2}\le 4\sqrt{{128}^2}=512$.

Do đó, S ≤ 512.

Dấu “=” xảy ra khi x² – 128 = 0 hay x = $8\sqrt{2}$ (0 < x < 16).

Vậy diện tích giấy màu cần sử dụng nhiều nhất là 512 cm².

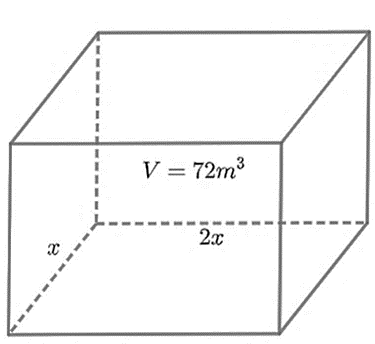
Bài 6. Bác Sơn muốn xây một bể chứa nước có dạng hình hộp chữ nhật không nắp có thể tích bằng 72 m³. Đáy bể có dạng hình chữ nhật với chiều rộng là x (m), chiều dài gấp đôi chiều rộng. Bác Sơn muốn phần diện tích cần xây (bao gồm diện tích xung quanh và diện tích đáy bể) là nhỏ nhất để tiết kiệm chi phí thì x phải bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?

A. x = 3,78 m.

B. x = 3,8 m.

C. x = 4,7 m.

D. x = 3,77 m.

Hướng dẫn giải

Đáp án đúng là: A

Chiều dài của đáy bể là 2x (m).

Diện tích đáy của bể là 2x² (m²).

Chiều cao của bể là: $\frac{72}{2x^2}=\frac{36}{x^2}$ (m²).

Diện tích xung quanh của bể là 2. $\frac{36}{x^2}$.(x + 2x) = $\frac{216}{x}$(m²).

Diện tích cần xây bằng tổng diện tích xung quanh và diện tích đáy của bể và bằng: $\frac{216}{x}$ + 2x² (m²).

Do x là chiều rộng của bể nên x > 0, áp dụng bất đẳng thức Cauchy ta có:

$2x^2+\frac{216}{x}=2x^2+\frac{108}{x}+\frac{108}{x}\ge 3\sqrt[3]{2x^2\cdot \frac{108}{x}\cdot \frac{108}{x}}$

Suy ra 2x² + $\frac{216}{x}$ ≥ 3$\sqrt[3]{23328}$ ≈ 3,78 m.

Vậy muốn diện tích cần xây là tiết kiệm chi phí nhất thì x ≈ 3,78 m.

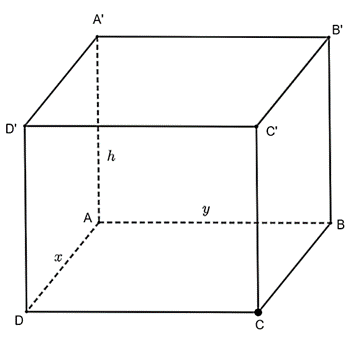
Bài 7. Nam làm một chiếc hộp không nắp dạng hình hộp chữ nhật bằng bìa carton có thể tích 3 dm³. Biết tỉ số giữa chiều cao h và chiều rộng đáy y bằng 4. Xác định chiều dài x để lượng bìa cần sử dụng là ít nhất.

A. $\frac{27}{2}$ dm.

B. $\frac{4}{3}$ dm.

C. $\frac{3}{4}$dm.

D. $\frac{1}{2}$dm.

Hướng dẫn giải

Đáp án đúng là: B

Theo đề bài, tỉ số giữa chiều cao h và chiều rộng đáy y bằng 4, suy ra h = 4y.

Thể tích khối hộp 3 dm³ nên xyh = 3 (dm³) hay 4xy² = 3 (dm³), suy ra x = $\frac{3}{4y^2}$.

Do chiếc hộp không nắp, nên diện tích bìa cần dùng là tổng diện tích đáy hộp và diện tích xung của hộp.

Ta có:

$S=xy+2h\left(x+y\right)=\frac{3}{4y^2}.y+2.4y.\left(\frac{3}{4y^2}+y\right)$.

$=\frac{3}{4y}+\frac{6}{y}+8y^2=\frac{27}{4y}+8y^2=\frac{27}{8y}+\frac{27}{8y}+8y^2$

Do y là chiều rộng của hộp nên y > 0.

Do đó, áp dụng bất đẳng thức Cauchy cho cả ba đều số không âm, ta được:

$\frac{27}{8y}+\frac{27}{8y}+8y^2\ge 3\sqrt[3]{\frac{27}{8y}.\frac{27}{8y}.8y^2}$suy ra S ≥ $\frac{27}{2}$.

Dấu “=” xảy ra khi $\frac{27}{8y}=8y^2$, suy ra y = $\frac{3}{4}$ (dm).

Do đó, $x=\frac{3}{4y^2}=\frac{3}{4.{\left(\frac{3}{4}\right)}^2}=\frac{4}{3}\left(\text{dm}\right)$

Vậy lượng bìa cần dùng ít nhất có diện tích là $\frac{27}{2}$ (dm²) khi chiều dài

x = $\frac{4}{3}$ (dm).

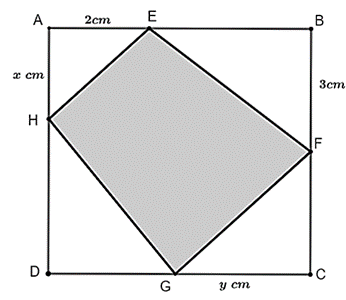
Bài 8. Cho một mảnh giấy hình vuông ABCD cạnh 6 cm. Gọi E, F lần lượt là hai điểm nằm trên cạnh AD và BC sao choAE = 2cm; BF = 3 cm. Bạn Nam muốn cắt một hình thang EFGH (như hình bên) sao cho hình thang đó có diện tích nhỏ nhất. Xác định vị trí của H trên cạnh AD để bạn Nam có thể thực hiện mong muốn của mình?

A. AH = $\frac{3\sqrt{2}}{2}$ cm.

B. AH = $\frac{3\sqrt{2}}{4}$ cm.

C. AH = $\frac{\sqrt{2}}{2}$ cm.

D. AH = $\frac{3}{2}$ cm.

Hướng dẫn giải

Đáp án đúng là: A

Diện tích hình vuông ABCD là 6² = 36 (cm²).

Diện tích tam giác BEF là $\frac{1}{2}$.3.(6 – 2) = 6 (cm²).

Diện tích hình thang EFGH là:

S_ABCD − S_BEF – S_AHE – S_DHG – S_CGF = 30 – (S_AHE + S_DHG + S_CGF).

Để diện tích hình thang EFGH nhỏ nhất thì S_AHE + S_HDG + S_CGF có diện tích lớn nhất.

Ta có: S_AHE + S_HDG + S_CGF = $\frac{1}{2}$.2x + $\frac{1}{2}$(6 – x)(6 – y) + $\frac{1}{2}$.3y

= 2x + (6 – x)(6 – y) + 3y

= 2x + 36 – 6y – 6x + xy + 3y

= 36 + xy – 4x – 3y.

Xét ∆AEH và ∆CGF, có: $\widehat{EAH}=\widehat{GCF}$ = 90° và $\widehat{AEH}=\widehat{CGF}$ (do EFGH là hình thang).

Suy ra ∆AEH ᔕ ∆CGF (g-g) nên $\frac{AH}{CF}=\frac{AE}{CG}$ hay $\frac{2}{y}=\frac{x}{3}$ do đó xy = 6 hay y = $\frac{6}{x}.$

Từ đó, ta có: 2(S_AHE + S_HDG + S_CGF) = 21 – $\left(2x+\frac{9}{x}\right)$.

Để thỏa mãn yêu cầu bài toán thì 2x + $\frac{9}{x}$ đạt giá trị nhỏ nhất.

Áp dụng bất đẳng thức Cauchy, ta có: $2x+\frac{9}{x}\ge 2\sqrt{2x.\frac{9}{x}}=6\sqrt{2}$

Dấu “=” xảy ra khi 2x = $\frac{9}{x}$ hay 2x² = 9 khi x = $\frac{3\sqrt{2}}{2}$.

Do đó, S_AHE + S_HDG + S_CGF = 21 – 6$\sqrt{2}$ và

S_EFGH = 30 – 21 + 6$\sqrt{2}$ = 9 + 6$\sqrt{2}$ (cm²).

Vậy AH = x = $\frac{3\sqrt{2}}{2}$ (cm²) thì diện tích hình thang EFGH đạt giá trị nhỏ nhất.

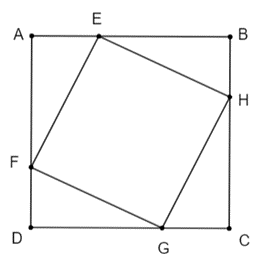
Bài 9. Bác An có mảnh vườn hình vuông ABCD có cạnh bằng 4 m. Ở bốn góc vườn, bác An muốn trồng hoa vào các phần đất hình tam giác vuông bằng nhau (hình vẽ). Hãy tính khoảng cách từ góc vườn A đến vị trí E sao cho tứ giác EFGH có chu vi nhỏ nhất.

A. $8\sqrt{2}$ m.

B. 2 m.

C. 3 m.

D. 4 m.

Hướng dẫn giải

Đáp án đúng là: B

Gọi độ dài của đoạn AE = x (0 < x < 4) (m) suy ra độ dài của đoạn

EB = 4 – x (m).

Theo đề, các phần đất hình tam giác bằng nhau, nên ta có:

AE = BH = GC = DF = x (m) và BE = CH = GD = AF = 4 – x (m).

Áp dụng định lí Pythagore vào tam giác AEF vuông tại A, ta có:

AE² + AF² = EF²

2x² – 8x + 16 = EF²

Suy ra EF = $\sqrt{2x^2-8x+16}=\sqrt{2\left(x^2-4x+4\right)+8}=\sqrt{2{\left(x-2\right)}^2+8}$ (m).

Do các phần hình tam giác có diện tích bằng nhau nên ta có:

FG = GH = HE = EF = $\sqrt{2{\left(x-2\right)}^2+8}$ (m).

Suy ra, chu vi tứ giác EFGH nhỏ nhất khi $\sqrt{2{\left(x-2\right)}^2+8}$ nhỏ nhất.

Với mọi 0 < x < 4, ta có:

2(x – 2)² ≥ 0

2(x – 2)² + 8 ≥ 8

$\sqrt{2{\left(x-2\right)}^2+8}$≥ $\sqrt{8}$

$4\sqrt{2{\left(x-2\right)}^2+8}$≥ $4\sqrt{8}$

$4\sqrt{2{\left(x-2\right)}^2+8}$≥ $8\sqrt{2}$.

Do đó, chu vi tứ giác EFGH nhỏ nhất bằng (m) khi x – 2 = 0 hay x = 2 (m).

Vậy khoảng cách từ A đến E bằng 2 m thì tứ giác EFGH có chu vi nhỏ nhất.

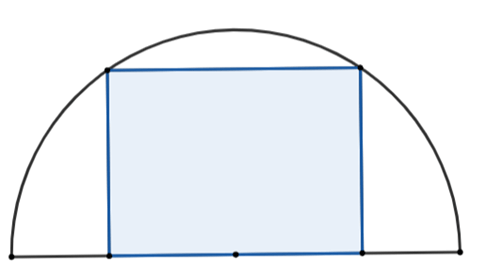
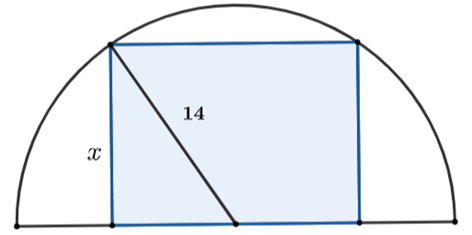
Bài 10.Một khu đất có dạng nửa hình tròn với bán kính là 14 m Người ta muốn xây dựng một khu vui chơi hình chữ nhật nội tiếp nửa đường tròn (như hình vẽ). Biết rằng một cạnh của hình chữ nhật nằm dọc trên đường kính của nửa đường tròn. Tính diện tích lớn nhất của khu vui chơi có thể xây dựng.

A. 169 m².

B. 196 m².

C. 144 m².

D. 225 m².

Hướng dẫn giải

Đáp án đúng là: B

Gọi x là độ dài cạnh hình chữ nhật không nằm dọc theo đường kính đường tròn (0 < x < 14).

Khi đó, độ dài cạnh của hình chữ nhật không nằm dọc trên đường tròn là: $2\sqrt{{14}^2-x^2}$(m).

Diện tích hình chữ nhật là S = 2x$\sqrt{{14}^2-x^2}$(m²).

Ta có: S² = 4x²(196 – x²) = −4x⁴ + 4x².196 – 196² + 196² = −(2x² – 196)² + 196²

Nhận thấy –(2x² – 196)² ≤ 0, do đó –(2x² – 196)² + 196² ≤ 196².

Suy ra S² ≤ 196², do đó S ≤ $\sqrt{{196}^2}$ hay S ≤ 196 m².

Dấu “=” xảy ra khi –(2x² – 196)² = 0 hay x = $7\sqrt{2}$ (m).

Vậy diện tích lớn nhất của khu vui chơi đó là 196 m².

Xem thêm các dạng bài tập Toán 9 hay, chi tiết khác:

• Chứng minh bất đẳng thức
• Nhận biết bất phương trình bậc nhất một ẩn
• Giải bất phương trình bậc nhất cơ bản
• Bất phương trình bậc nhất biến đổi đặc biệt
• Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn

• Hơn 20.000 câu trắc nghiệm Toán,Văn, Anh lớp 9 có đáp án

---