Một số bài toán thực tế liên quan đến hình cầu lớp 9 (cách giải + bài tập)

Chuyên đề phương pháp giải bài tập Một số bài toán thực tế liên quan đến hình cầu lớp 9 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Một số bài toán thực tế liên quan đến hình cầu.

Một số bài toán thực tế liên quan đến hình cầu lớp 9 (cách giải + bài tập)

1. Phương pháp giải

Để giải bài toán thực tế liên quan đến hình cầu, trước hết ta cần xác định bán kính của hình cầu bằng cách mô hình hóa, sau đó sử dụng các công thức tính diện tích, thể tích kết hợp các kiến thức liên quan để giải quyết bài toán.

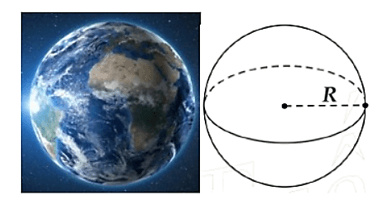
− Diện tích mặt cầu có bán kính R là: S = 4πR².

− Thể tích của hình cầu có bán kính R là: V = $\frac{4}{3}$πR³.

2. Ví dụ minh họa

Ví dụ 1. Trái Đất, hành tinh chúng ta đang sống, dạng hình cầu có bán kính là 6 370 km. Biết rằng 29% diện tích bề mặt Trái Đất không bị bao phủ bởi nước bao gồm núi, sa mạc, cao nguyên, đồng bằng và các địa hình khác. Tính diện tích bề mặt Trái Đất bị bao phủ bởi nước (Lấy π = 3,14; kết quả làm tròn đến chữ số hàng đơn vị).

Hướng dẫn giải

Diện tích bề mặt Trái Đất là: S = 4πR² = 4.3,14.6370² = 509 645 864 (km²).

Diện tích bề mặt Trái Đất bị bao phủ bởi nước là:

(100% − 29%).509 645 864 ≈ 361 848 563 (km²).

Ví dụ 2. Một quả bóng bằng da có đường kính 22 cm. Tính diện tích da cần dùng để làm quả bóng nếu không tính tỉ lệ hao hụt (lấy π = 3,14).

Hướng dẫn giải

Bán kính của quả bóng này là: 22 : 2 = 11 (cm).

Diện tích da cần dùng để làm quả bóng chính là diện tích bề mặt của quả bóng hình cầu.

Do đó, diện tích da cần dùng để làm quả bóng là: 4π.11² = 1 519,76 cm².

3. Bài tập tự luyện

Câu 1. Bạn Nam được tặng một quả bóng đá có đường kính 24 cm (hình vẽ).

Em hãy giúp bạn ấy tính xem cần bao nhiêu mét vuông da để chế tạo quả bóng, giả sử rằng diện tích các mép nối không đáng kể, lấy π = 3,14.

A. 7 234,56 cm².

B. 1 808,64 cm².

C. 150,72 cm².

D. 452,16 cm².

Hướng dẫn giải

Đáp án đúng là: B

Bán kính của quả bóng là: 24 : 2 = 12 (cm).

Diện tích da cần dùng chính là tính diện tích bề mặt hình cầu.

Do đó, ta có diện tích da cần dùng để chế tạo bóng là: 4.3,14.12² = 1 808,64 (cm²).

Câu 2. Một quả pha lê hình cầu có diện tích mặt cầu bằng 144π cm². Tính thể tích quả pha lê đó.

A. 288 cm³.

B. 288π cm³.

C. 36 cm³.

D. 36π cm³.

Hướng dẫn giải

Đáp án đúng là: B

Bán kính của quả pha lê đó là: $\sqrt{144\pi :4\pi }$ = 6 (cm)

Thể tích của quả pha lê đó là: $\frac{4}{3}\pi {.6}^3=288\pi$ (cm³).

Sử dụng dữ liệu của bài toán dưới đây để trả lời Câu 3, 4.

Một tháp nước có bể chứa hình cầu, đường kính bên trong của bể đo được là 6 m.

Câu 3. Thể tích của tháp nước đó là

A. 288 m³.

B. 288π m³.

C. 36 m³.

D. 36π m³.

Hướng dẫn giải

Đáp án đúng là: D

Bán kính của tháp nước đó là;  6 : 2 = 3 (m).

Thể tích của tháp nước đó là: $\frac{4}{3}\pi {.3}^3=36\pi$ (m³).

Câu 4. Biết rằng lượng nước đựng đầy trong bể đủ dùng cho một khu dân cư trong 5 ngày. Biết khu dân cư có 1304 người. Hỏi trong một ngày bình quân mỗi người dùng hết bao nhiêu lít nước? (lấy π = 3,14; biết 1 m³ = 1 000 lít, kết quả làm tròn đến hàng phần trăm)

A. 17,34 lít.

B. 16,87 lít.

C. 17,43 lít.

D. 16,78 lít.

Hướng dẫn giải

Đáp án đúng là: A

Ta có, với π = 3,14 thì thể tích của bể đó là: 3,14.36 = 113,04 (m³)

Đổi 113,04 m³ = 113 040 lít.

Do đó, một ngày khu dân cư đó dùng hết số nước là:

113 040 : 5 = 22 608 (lít)

Suy ra một ngày bình quân mỗi người dùng hết số lít nước là:

22 608 : 1304 ≈ 17,34 (lít).

Câu 5. Một quả bóng rổ (loại số 7 cho nam) và một quả bóng tennis. Biết rằng diện tích bề mặt của quả bóng rổ khoảng 1 884,75 và bán kính của quả bóng rổ gấp khoảng 2 lần đường kính của quả bóng tennis.

Hỏi diện tích bề mặt của quả bóng tennis đó là bao nhiêu centimet vuông?

(lấy π = 3,14 và làm tròn kết quả cuối cùng đến hàng phần mười).

A. 116,8 cm².

B. 118 cm².

C. 117,8 cm².

D. 118,7 cm².

Hướng dẫn giải

Đáp án đúng là: C

Gọi R là bán kính của quả bóng rổ (R > 0).

Ta có công thức tính diện tích bề mặt của quả bóng rổ hình cầu là:

S = 4πR² (cm²).

Theo bài, diện tích bề mặt của quả bóng rổ khoảng 1 884,75 cm² nên ta có:

4πR² = 1 884,75 nên R² = 1 884,75 : 4π = $\frac{7539}{16\pi }$.

Suy ra R = $\sqrt{\frac{7539}{16\pi }}=\frac{\sqrt{7539\pi }}{4\pi }$ (cm).

Vì bán kính của quả bóng rổ gấp khoảng 2 lần đường kính của quả bóng tennis nên đường kính của quả bóng tennis là: $\frac{\sqrt{7539\pi }}{4\pi }$ : 2 = $\frac{\sqrt{7539\pi }}{8\pi }$ (cm).

Do đó, bán kính của quả bóng tennis là: $\frac{\sqrt{7539\pi }}{8\pi }$ : 2 = $\frac{\sqrt{7539\pi }}{16\pi }$ (cm).

Suy ra diện tích bề mặt của quả bóng tennis đó là:

4π. ${\left(\frac{\sqrt{7539\pi }}{16\pi }\right)}^2=\frac{4\pi .7539\pi }{256{\pi }^2}=\frac{7539}{64}\approx 117,8$ (cm ²).

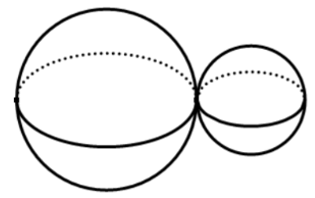
Câu 6. Một khối gỗ đồ chơi gồm hai khối cầu (H₁) và (H₂) tiếp xúc với nhau, lần lượt có bán kính tương ứng là r₁, r₂ thỏa mãn r₂ = $\frac{1}{2}$r₁.

Biết rằng thể tích của toàn bộ khối đồ chơi bằng 180π cm³. Tính thể tích của khối cầu (H₁).

A. 160 cm³.

B. 160π cm³.

C. 20 cm³.

D. 20π cm³.

Hướng dẫn giải

Đáp án đúng là: B

Thể tích khối H₁ là: $V_1=\frac{4}{3}\pi .r_1^3$ (cm³).

Thể tích khối H₂ là: $V_2=\frac{4}{3}\pi .r_2^3=\frac{4}{3}\pi .{\left(\frac{1}{2}{r}_1\right)}^3=\frac{1}{6}\pi r_1^3$ (cm³).

Mà thể tích toàn bộ khối đồ chơi bằng 180π cm³  nên ta có:

$\frac{4}{3}\pi .r_1^3+\frac{1}{6}\pi r_1^3=180\pi$ hay $\frac{3}{2}\pi r_1^3=180\pi$ nên $r_1^3=120$.

Suy ra thể tích khối cầu H₁ là: $V_1=\frac{4}{3}\pi .r_1^3=\frac{4}{3}\pi .120=160\pi$ (cm³).

Sử dụng dữ kiện của bài toán dưới đây để trả lời Câu 7, 8.

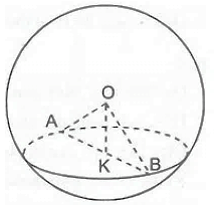
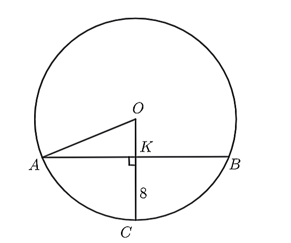
Người ta cắt một quả địa cầu cũ bằng một mặt phẳng theo một vĩ tuyến và được một phần có hình dạng chảo, đường kính miếng chảo là 24 cm và độ sâu nhất của chảo là 8 cm.

Câu 7. Bán kính của quả địa cầu đó là

A. 8 cm.

B. 4 cm.

C. 12 cm.

D. 13 cm.

Hướng dẫn giải

Đáp án đúng là: D

Mặt cắt là hình tròn tâm K đường kính AB (OC ⊥ AB tại K).

Theo đề, ta có KC = 8 cm, AB = 24 cm.

Do đó, KA = KB = 24 : 2 = 12 cm.

Gọi R là bán kính của quả địa cầu.

Áp dúng định lý Pythagore vào tam giác OAK, có:

OK² + AK² = OA² nên (R – 8)² + 12² = R²

Suy ra R² – 16R + 64 + 144 = R² hay 16R = 208 suy ra R = 13 (cm).

Câu 8. Diện tích bề mặt của quả địa cầu là

A. 676 cm².

B. 676π cm².

C. $\frac{8788}{3}\pi$ cm².

D. $\frac{8788}{3}$ cm².

Hướng dẫn giải

Đáp án đúng là: B

Diện tích bề mặt của quả địa cầu là:

S = 4πR² = 4π.13² = 676π (cm²).

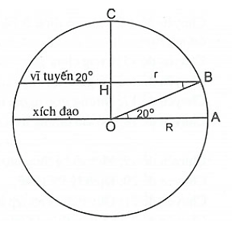
Câu 9. Vĩ độ của Thanh Hóa là 20° Bắc được biểu diễn trong hình vẽ dưới đây.

Tính độ dài vĩ tuyến qua Thanh Hóa, biết bán kính Trái Đất là 6370 km.

(Kết quả làm tròn đến hàng phần mười)

A. 2178,7  km.

B. 5985,8 km.

C. 2187,7 km.

D. 5958,8 km.

Hướng dẫn giải

Đáp án đúng là: A

Gọi R là bán kính Trái đất, r là bán kính của vĩ tuyến 20° qua Thanh Hóa.

Ta có: $\widehat{BOA}=\widehat{OBH}=20°$.

Xét tam giác HBO vuông tại H có $\widehat{OBH}=20°$, OB = 6370 km.

Do đó, HO = sin20°.6370 ≈ 2178,7 (km).

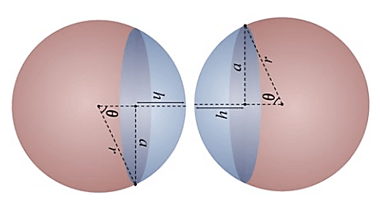
Câu 10. Công ty vàng bạc đá quý muốn làm một món đồ trang sức có hạng hai hình cầu bằng nhau và giao với nhau như hình vẽ. Khối cầu có bán kính 25 cm khoảng cách giữa hai tâm hình cầu là 40 cm. Giá mạ vàng 1 m² là 470 000 đồng. Nhà sản xuất muốn mạ vàng xung quanh món đồ trang sức đó.

Tính số tiền cần dùng để mạ vàng khối trang sức  đó. (Lấy π = 3,14).

A. 332 500 đồng.

B. 665 000 đồng.

C. 664 110 đồng.

D. 332 055 đồng

Hướng dẫn giải

Đáp án đúng là: C

(Phần màu nhạt là phần giao nhau của hai khối cầu).

Gọi h là chiều cao của chỏm cầu.

Ta có: $h=\frac{2R-d}{2}=\frac{2.25-40}{2}=5$ cm.

(d là khoảng cách giữa hai tâm)

Diện tích xung quanh của chỏm cầu làm: S = 2πRh.

Vì hai khối cầu bằng nhau nên hai hình chỏm cầu bằng nhau.

Diện tích xung quanh khối trang sức bằng hai lần diện tích xung quanh khối cầu trừ hai lần diện tích xung quanh chỏm cầu.

Ta có diện tích xung quanh khối cầu là: 4πR² = 2 500π (cm²).

Diện tích xung quanh chỏm cầu là: 2πRh = 2.π.25.5 = 250π (cm²).

Do đó, diện tích xung quanh khối trang sức là:

2.2 500π – 2.250π = 4 500π = 14 130 (cm²).

Đổi 14 130 cm² = 1,413 m².

Số tiền cần dùng để mạ vàng khối trang sức là:

1,413.470 000 = 664 110 (đồng).

Xem thêm các dạng bài tập Toán 9 hay, chi tiết khác:

• Một số bài toán thực tế liên quan đến hình nón
• Tính diện tích mặt ngoài, thể tích của hình hỗn hợp có liên quan đến hình trụ, hình nón
• Nhận biết hình cầu và xác định tâm, bán kính của hình cầu
• Tính diện tích mặt cầu và thể tích của hình cầu
• Tính diện tích mặt ngoài, thể tích của hình hỗn hợp có liên quan đến hình cầu

• Hơn 20.000 câu trắc nghiệm Toán,Văn, Anh lớp 9 có đáp án

---