Tính diện tích mặt ngoài, thể tích của hình hỗn hợp có liên quan đến hình cầu lớp 9 (cách giải + bài tập)
Chuyên đề phương pháp giải bài tập Tính diện tích mặt ngoài, thể tích của hình hỗn hợp có liên quan đến hình cầu lớp 9 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Tính diện tích mặt ngoài, thể tích của hình hỗn hợp có liên quan đến hình cầu.
Tính diện tích mặt ngoài, thể tích của hình hỗn hợp có liên quan đến hình cầu lớp 9 (cách giải + bài tập)
(199k) Xem Khóa học Toán 9 KNTTXem Khóa học Toán 9 CDXem Khóa học Toán 9 CTST
1. Phương pháp giải
Để tính diện tích mặt ngoài, thể tích của hình hỗn hợp có liên quan đến hình cầu, ta có thể làm như sau:
Bước 1. Xác định những hình khối có trong hình hỗn hợp đó.
Bước 2. Xác định bán kính, chiều cao, … của các hình khối.
Bước 3. Sử dụng các công thức tính diện tích, thể tích hình khối để tính từng bộ phận của hình hỗn hợp rồi cộng vào (hoặc trừ đi), từ đó giải quyết yêu cầu bài toán.
2. Ví dụ minh họa
Ví dụ 1. Một khối cầu pha lê gồm một hình cầu (H1) bán kính R và một hình nón (H2) có bán kính đáy và đường sinh lần lượt là r, l thỏa mãn r = l và l = R xếp chồng lên nhau. Biết tổng diện tích mặt cầu (H1) và diện tích toàn phần của hình nón (H2) là 91 cm2.
Tính diện tích của mặt cầu (H1).
Hướng dẫn giải
Ta có: r = R = R.
Diện tích mặt cầu S1 = 4πR2.
Diện tích toàn phần của hình nón S2 = πrl + πr2 = .
Theo giả thiết, ta có: 4πR2 + = 91 hay = 91 suy ra πR2 = 16.
Do đó, diện tích mặt cầu (H1) là: S1 = 4πR2 = 64 cm2.
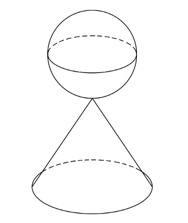
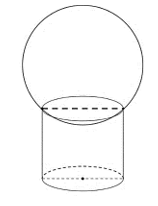
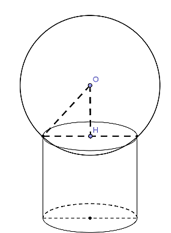
Ví dụ 2. Cho một hình cầu và hình trụ ngoại tiếp nó (đường kính đáy và chiều cao của hình trụ bằng bao nhau và bằng đường kính của hình cầu).
Tính tỉ số giữa diện tích mặt cầu và diện tích toàn phần của hình trụ.
Hướng dẫn giải
Chiều cao của hình trụ là h = 2R.
Diện tích mặt cầu là: S1 = 4πR2.
Diện tích toàn phần của hình trụ là:
Stp = Sxq + 2Sđáy = 2πR(h + R) = 2πR(2R + R) = 6πR2.
Do đó, tỉ số giữa diện tích mặt cầu và diện tích toàn phần của hình trụ là
3. Bài tập tự luyện
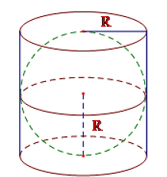
Câu 1. Cho một hình cầu nội tiếp trong hình trụ. Biết rằng chiều cao của hình trụ bằng ba lần bán kính đáy và bán kính đáy của hình trụ bằng bán kính đáy của hình cầu. Tính tỉ số giữa thể tích hình cầu và thể tích hình trụ.
A.
B.
C.
D. 2
Hướng dẫn giải
Đáp án đúng là: B
Từ đề bài, ta có chiều cao hình trụ là h = 3R với R là bán kính của hình cầu và cũng là bán kính đáy của hình trụ
Thể tích hình cầu VC = .
Thể tích hình trụ VT = πR2.3R = 3πR3.
Tỉ số thể tích hình cầu và thể tích hình trụ là .
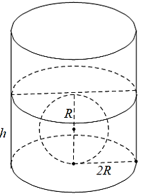
Câu 2. Người ta thả một viên bi có dạng hình cầu có bán kính 2,7 cm vào một chiếc cốc hình trụ đang chứa nước. Biết rằng bán kính của phần trong đáy cốc bằng 5,4 cm và chiều cao của mực nước ban đầu trong cốc bằng 4,5 cm.
Khi đó chiều cao của mực nước trong cốc là bao nhiêu?
A. 4,2 cm.
B. 3,6 cm.
C. 2,7 cm.
D. 5,4 cm.
Hướng dẫn giải
Đáp án đúng là: D
Gọi R = 2,7 cm là bán kính của viên bi. Ta có bán kính phần trong đáy cốc là 3R.
Thể tích nước ban đầu là: V1 = π(2R)2.4,5 = 18πR2.
Thể tích viên bi là V2 = .
Thể tích nước sau khi thả viên bi là: V = V1 + V2 = 18πR2 + = 2πR2.
Gọi h là chiều cao mực nước sau khi thả viên bi vào.
Ta có: V = 2πR2 = π(2R)2.h
Suy ra h = 2πR2 (cm).
Câu 3. Một trái banh và một chiếc chén hình trụ có cùng chiều cao. Người ta đặt trái banh lên hình trụ thấy phần ở bên ngoài của quả bóng có chiều cao bằng chiều cao của nó.
Gọi V1, V2 lần lượt là thể tích của quả bóng và chiếc chén, tính tỉ số .
A.
B.
C.
D.
Hướng dẫn giải
Đáp án đúng là: A
Gọi R là bán kính mặt cầu, r, h lần lượt là bán kính đáy và chiều cao hình trụ.
Theo bài, ta có: h = 2R và r = .
Ta có: V1 = ; V2 = πr2h = π. .2R = .
Do đó, .
Sử dụng dữ liệu của bài toán dưới đây để trả lời Câu 4, 5.
Một hộp đựng bóng tennis có dạng hình trụ chứa vừa khít ba quả bóng tennis xếp theo chiều dọc. Các quả bóng tennis có dạng hình cầu, đường kính 6,4 cm.
Câu 4. Tính thể tích hộp đựng bóng (bỏ qua bề dày của vỏ hộp, làm tròn kết quả đến hàng đơn vị của cm3)
A. 618 cm3.
B. 206 cm3.
C. 618π cm3.
D. 206π cm3.
Hướng dẫn giải
Đáp án đúng là: A
Chiều cao hình trụ là: 6,4.3 = 19,2 cm.
Đường kính hình trụ chính bằng đường kính quả bóng và bằng 6,4 cm.
Bán kính của hộp là: 6,4 : 2 = 3,2 cm.
Thể tích hộp đựng bóng là: π.(3,2)2.19,2 ≈ 618 (cm3).
Câu 5. Tính thể tích bên trong hộp đựng bóng không bị chiếm bởi ba quả bóng tennis.
A. 412 cm3.
B. 206 cm3.
C. 206π cm3.
D. 412π cm3.
Hướng dẫn giải
Đáp án đúng là: B
Bán kính của quả bóng tennis là: R2 = 6,4 : 2 = 3,2 (cm).
Thể tích của ba quả bóng tennis có dạng hình cầu là:
V2 = 3. ≈ 412 cm3.
Thể tích phần bên trong hộp đựng bóng không bị chiếm bởi ba quả bóng tennis là:
618 – 412 = 206 cm3.
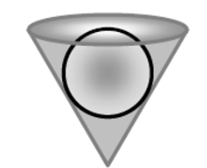
Câu 6. Thả một quả cầu đặc có bán kính 3 cm vào một vật hình nón (có đáy nón không kín) (như hình vẽ bên dưới). Cho biết khoảng cách từ tâm quả cầu đến đỉnh nón là 5 cm.
Tính thể tích (theo đơn vị cm3) phần không gian kín giới hạn bởi bề mặt quả cầu và bề mặt trong của vật hình nón.
A. cm3.
B. cm3.
C. cm3.
D. cm3.
Hướng dẫn giải
Đáp án đúng là: D
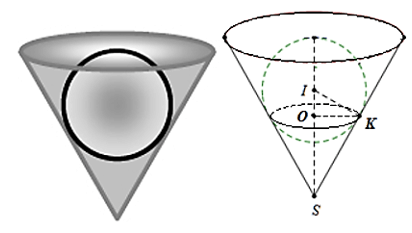
Xét hình nón và quả cầu như hình vẽ bên dưới.
Từ đề bài, ta có hình mình họa với O là tâm đường tròn giới hạn bởi mặt quả cầu và bề mặt trong hình nón; K là giao của mặt cắt tâm (O) với phần hình chóp, I là tâm mặt cầu và S là đỉnh của hình chóp.
Xét ∆KIS và ∆OIK, có:
và
Do đó, ∆KIS ᔕ ∆OIK nên hay OI = = (cm).
Thể tích của chỏm cầu tâm I bán kính OK là:
V2 = (cm3).
Thể tích hình nón có đỉnh S, đáy hình tròn tâm O, bán kính đáy OK là:
V1 = (cm3).
Thể tích phần không gian kín giỏi hạn bởi mặt cầu và bề mặt trong của vật hình nón là:
V1 – V2 = (cm3).
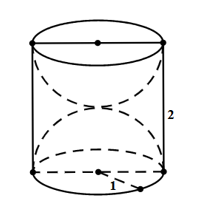
Câu 7. Một khối gỗ hình trụ xoay có bán kính đáy bằng 1, chiều cao bằng 2. Người ta khoét từ hai đầu khối gỗ hai nửa khối cầu mà đường tròn đáy của khối gỗ là đường tròn lớn của mỗi nửa hình cầu.
Tính tỉ số thể tích phần còn lại của khối gỗ và cả khối gỗ ban đầu.
A.
B.
C.
D.
Hướng dẫn giải
Đáp án đúng là: A
Hai nửa khối cầu ghép lại ta được một khối cầu có bán kính bằng 1.
Do đó, thể tích phần gỗ bị khoét là: .
Thể tích khối gỗ hình trụ ban đầu là: πr2h = 2π.
Do đó, thể tích còn lại của khối gỗ là: 2π − .
Suy ra tỉ số thể tích phần còn lại của khối gỗ so với với khối gỗ ban đầu là:
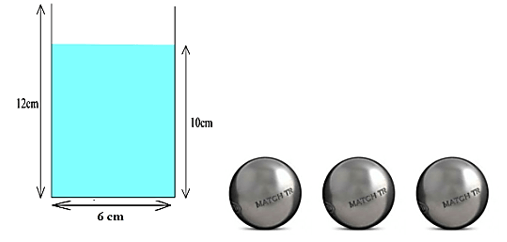
Câu 8. Một cốc nước có dạng hình trụ có đường kính đáy bằng 6 cm, chiều cao 12 cm và chứa một lượng nước cao 10 cm. Người ta thả từ từ 3 viên bi làm bằng thép đặc (không thấm nước) có đường kính bằng 2 cm vào cốc nước.
Hỏi mực nước trong cốc lúc này cao bao nhiêu?
A. cm
B. cm
C. 90 cm
D. cm
Hướng dẫn giải
Đáp án đúng là: D
Bán kính của viên bi là: R = cm.
Thể tích của một viên bi là: V1 = (cm3).
Do ba viên bi có cùng đường kính nên tổng thể tích của ba viên bi là:
V = 3V1 = 3. = 4π (cm3).
Diện tích của đáy cốc nước (hình tròn r = 3 cm) là:
S = π.r2 = π.32 = 9π (cm2).
Chiều cao của phần cốc không chứa nước là: 12 – 10 = 2 (cm).
Thể tích phần cốc không chứa nước (cốc hình trụ, diện tích phần đáy cũng là diện tích phần mặt phân cách giữa phần có nước và phần không có nước).
V' = S.h = 9π.2 = 18π (cm3).
Do thể tích phần cốc không chứa nước lớn hơn thể tích ba viên nên khi thả ba viên bi vào cốc thì nước không bị tràn ra ngoài.
Gọi x là chiều cao mực nước dâng lên sau khi thả 3 viên bi vào cốc, thể tích của 3 viên bi cũng là thể tích phần nước dâng lên ta có:
V = S.x hay 9π.x = 4π nên x = cm.
Vậy chiều cao của mực nước trong ống sau khi thả 3 viên bi là: 10 + = cm.
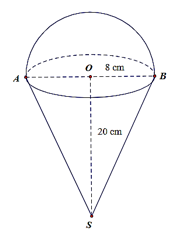
Câu 9. Người ta gắn một hình nón có bán kính đáy R = 8 cm, độ dài đường cao h = 20 cm vào một nửa hình cầu có bán kính bằng bán kính hình nón (theo hình bên dưới).
Tính giá trị gần đúng thể tích của hình tạo thành (kết quả làm tròn đến chữ số hàng đơn vị).
A. 2413 cm3.
B. 2413π cm3.
C. 2412 cm3.
D. 2412π cm3.
Hướng dẫn giải
Đáp án đúng là: A
Ta có thể tích của nửa hình cầu đó là: V1 = (cm3).
Thể tích hình nón là: V2 = (cm3).
Thể tích khối hình tạo thành là:
V = V1 + V2 = ≈ 2413 (cm3).
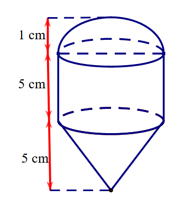
Câu 10. Cho hình khối dưới đây được tạo thành các khối hình cầu, hình trụ và hình nón (có cùng bán kính đáy).
Tính thể tích của các hình đó theo kích thước đã cho.
A. cm3.
B. cm3.
C. cm3.
D. cm3.
Hướng dẫn giải
Đáp án đúng là: C
Thể tích của phần khối nửa hình cầu là: V1 = (cm3).
Nhận thấy bán kính của các phần khối hình cầu, hình trụ và hình nón bằng nhau.
Do đó, thể tích phần hình trụ là: V2 = πr2h = π.12.5 = 5π (cm3).
Thể tích phần hình nón là: V3 = (cm3).
Suy ra thể tích của hình khối đã cho là: (cm3).
(199k) Xem Khóa học Toán 9 KNTTXem Khóa học Toán 9 CDXem Khóa học Toán 9 CTST
Xem thêm các dạng bài tập Toán 9 hay, chi tiết khác:
- Một số bài toán thực tế liên quan đến hình nón
- Tính diện tích mặt ngoài, thể tích của hình hỗn hợp có liên quan đến hình trụ, hình nón
- Nhận biết hình cầu và xác định tâm, bán kính của hình cầu
- Tính diện tích mặt cầu và thể tích của hình cầu
- Một số bài toán thực tế liên quan đến hình cầu
Tủ sách VIETJACK luyện thi vào 10 cho 2k11 (2026):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Loạt bài Chuyên đề: Lý thuyết - Bài tập Toán lớp 9 Đại số và Hình học có đáp án có đầy đủ Lý thuyết và các dạng bài được biên soạn bám sát nội dung chương trình sgk Đại số 9 và Hình học 9.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 9 Global Success
- Giải sgk Tiếng Anh 9 Smart World
- Giải sgk Tiếng Anh 9 Friends plus
- Lớp 9 Kết nối tri thức
- Soạn văn 9 (hay nhất) - KNTT
- Soạn văn 9 (ngắn nhất) - KNTT
- Giải sgk Toán 9 - KNTT
- Giải sgk Khoa học tự nhiên 9 - KNTT
- Giải sgk Lịch Sử 9 - KNTT
- Giải sgk Địa Lí 9 - KNTT
- Giải sgk Giáo dục công dân 9 - KNTT
- Giải sgk Tin học 9 - KNTT
- Giải sgk Công nghệ 9 - KNTT
- Giải sgk Hoạt động trải nghiệm 9 - KNTT
- Giải sgk Âm nhạc 9 - KNTT
- Giải sgk Mĩ thuật 9 - KNTT
- Lớp 9 Chân trời sáng tạo
- Soạn văn 9 (hay nhất) - CTST
- Soạn văn 9 (ngắn nhất) - CTST
- Giải sgk Toán 9 - CTST
- Giải sgk Khoa học tự nhiên 9 - CTST
- Giải sgk Lịch Sử 9 - CTST
- Giải sgk Địa Lí 9 - CTST
- Giải sgk Giáo dục công dân 9 - CTST
- Giải sgk Tin học 9 - CTST
- Giải sgk Công nghệ 9 - CTST
- Giải sgk Hoạt động trải nghiệm 9 - CTST
- Giải sgk Âm nhạc 9 - CTST
- Giải sgk Mĩ thuật 9 - CTST
- Lớp 9 Cánh diều
- Soạn văn 9 Cánh diều (hay nhất)
- Soạn văn 9 Cánh diều (ngắn nhất)
- Giải sgk Toán 9 - Cánh diều
- Giải sgk Khoa học tự nhiên 9 - Cánh diều
- Giải sgk Lịch Sử 9 - Cánh diều
- Giải sgk Địa Lí 9 - Cánh diều
- Giải sgk Giáo dục công dân 9 - Cánh diều
- Giải sgk Tin học 9 - Cánh diều
- Giải sgk Công nghệ 9 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 9 - Cánh diều
- Giải sgk Âm nhạc 9 - Cánh diều
- Giải sgk Mĩ thuật 9 - Cánh diều

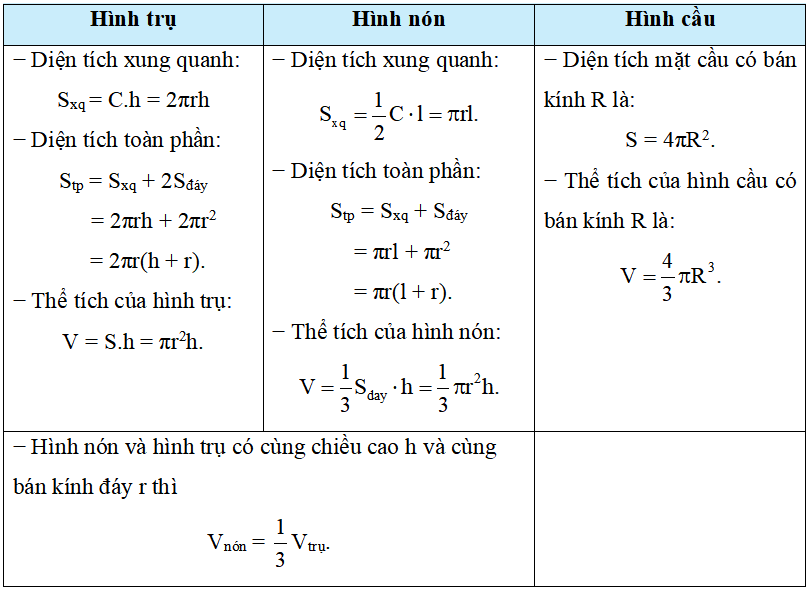





 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

