Tính xác suất của biến cố liên quan đến phép thử khi các kết quả của phép thử đồng khả năng lớp 9 (cách giải + bài tập)

Chuyên đề phương pháp giải bài tập Tính xác suất của biến cố liên quan đến phép thử khi các kết quả của phép thử đồng khả năng lớp 9 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Tính xác suất của biến cố liên quan đến phép thử khi các kết quả của phép thử đồng khả năng.

Tính xác suất của biến cố liên quan đến phép thử khi các kết quả của phép thử đồng khả năng lớp 9 (cách giải + bài tập)

1. Phương pháp giải

− Giả thiết  rằng các kết quả có thể xảy ra cùng một phép thử T là đồng khả năng. Khi đó, xác suất của biến cố E, kí hiệu P(E), bằng tỉ số giữa số kết quả thuận lợi cho biến cố và tổng số kết quả có thể xảy ra.

$P\left(E\right)=\frac{n\left(E\right)}{n\left(\Omega \right)}$.

Trong đó: n(E) là các kết quả thuận lợi cho E.

                 n(Ω) là số các kết quả có thể xảy ra.

− Để tính xác suất của biến cố E, ta thực hiện các bước sau:

Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử không gian mẫu Ω.

Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng.

Bước 3. Mô tả các kết quả thuận lợi cho biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E.

Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E và số phần tử không gian mẫu Ω.

− Chú ý: Trong một phép thử, hai kết quả được gọi là đồng khả năng nếu chúng có khả năng xảy ra như nhau.

+ Trong phép thử lấy vật (quả bóng, viên bi, …) nếu có giả thiết các vật có cùng kích thước và khối lượng thì mỗi vật đều có cùng khả năng được lựa chọn.

+ Trong phép thử gieo đồng xu (hoặc gieo xúc xắc), nếu có giả thiết đồng xu, xúc xắc là cân đối và đồng chất thì các mặt của đồng xu hay xúc xắc sẽ có cùng khả năng xuất hiện.

2. Ví dụ minh họa

Ví dụ 1. Một hộp có 20 viên bi với kích thước và khối lượng như nhau. Bạn Ngân viết lên các viên bi đó các số 1, 2, 3,…, 20; hai viên bi khác nhau thì viết hai số khác nhau.

Xét phép thử “Lấy ngẫu nhiên một viên bi trong hộp”.

a) Xác định không gian mẫu của phép thử.

b) Xác định các kết quả thuận lợi của biến cố: “Số xuất hiện trên viên bi được lấy ra chia 7 dư 1”.

c) Tính xác suất của biến cố: “Số xuất hiện trên viên bi được lấy ra chia 7 dư 1”.

Hướng dẫn giải

a) Ta có không gian mẫu của phép thử là: n(Ω) = {1; 2; 3;…..; 20}. Do đó, số phần tử của không gian mẫu là 20.

b) Kết quả thuận lợi cho biến cố “Số xuất hiện trên viên bi được lấy ra chia 7 dư 1” là: {1; 8; 15}.

Do đó, có ba kết quả thuận lợi cho biến cố trên.

c) Xác suất của biến cố “Số xuất hiện trên viên bi được lấy ra chia 7 dư 1” là $\frac{3}{20}$.

Ví dụ 2. Viết ngẫu nhiên một số tự nhiên lớn hơn 499 và nhỏ hơn 1 000.

a) Xác định không gian mẫu của phép thử.

b) Xác định kết quả thuận lợi của biến cố A: “Số tự nhiên viết ra chia hết cho 100”.

c) Tính xác suất của biến cố B: “Số tự nhiên viết ra là lập phương của một số tự nhiên”.

Hướng dẫn giải

a) Số các số tự nhiên lớn hơn 499 và nhỏ hơn 1 000 (tức từ từ 500 đến 999) là:

(999 – 500) : 1 + 1 = 500 (số)

Do đó n(Ω) = {500; 501; …; 998; 999} và có 500 phần tử.

b) Số kết quả thuận lợi cho biến cố A: “Số tự nhiên viết ra chia hết cho 100” là 500; 600; 700; 800; 900.

Do đó, có 5 kết quả thuận lợi cho biến cố trên.

c) Số kết quả thuận lợi cho biến cố B: “Số tự nhiên viết ra là lập phương của một số tự nhiên” là 512; 729. Do đó, có 2 kết quả thuận lợi cho biến cố trên.

Xác suất của biến cố B là: $\frac{2}{500}=\frac{1}{125}$

3. Bài tập tự luyện

Câu 1. Gieo hai đồng xu cân đối và đồng chất. Xác suất của biến cố “Hai đồng xu đều xuất hiện mặt sấp” là

A. $\frac{1}{4}.$

B. 1

C. $\frac{3}{4}.$

D. $\frac{1}{2}.$

Hướng dẫn giải

Đáp án đúng là: A

Số không gian mẫu của phép thử là: Ω = {SS, SN, NS, NN} nên n(Ω) = 4.

Kết quả thuận lợi cho biến cố “Hai đồng xu đều xuất hiện mặt sấp” là: SS.

Do đó, có 1 kết quả thuận lợi cho biến cố trên.

Suy ra xác suất của biến cố này là: $\frac{1}{4}.$

Câu 2. Gieo một con xúc xắc cân đối và đồn chất. Xác suất của biến cố “Xuất hiện mặt có số chấm là bội của 3” là

A. $\frac{1}{6}.$

B. $\frac{1}{3}.$

C. $\frac{1}{2}.$

D. $\frac{2}{3}.$

Hướng dẫn giải

Đáp án đúng là: B

Không gian mẫu Ω = {mặt 1 chấm, mặt 2 chấm, mặt 3 chấm, mặt 4 chấm, mặt 5 chấm; mặt 6 chấm}

Do đó, số phần tử của không gian mẫu là 6 phần tử.

Kết quả thuận lợi cho biến cố “Xuất hiện mặt có số chấm là 3” là: mặt 3 chấm, mặt 6 chấm.

Suy ra xác suất của biến cố đó là: $\frac{2}{6}=\frac{1}{3}.$

Câu 3. An có 10 tấm thẻ cùng loại được đánh số từ 1 đến 10. An rút ngẫu nhiên một tấm thẻ. Xác suất của biến cố “Lấy được tấm thẻ ghi số có hai chữ số” là

A. $\frac{1}{10}.$

B. $\frac{1}{5}.$

C. $\frac{9}{10}.$

D. 1.

Hướng dẫn giải

Đáp án đúng là: A

Số phần tử của không gian mẫu là 10 phần tử.

Kết quả thuận lợi cho biến cố “An lấy được tấm thẻ ghi số có hai chữ số” là thẻ số 10.

Do đó, có 1 kết quả thuận lợi cho biến cố trên.

Xác suất của biến cố đó là: $\frac{1}{10}.$

Câu 4. Nam gieo một con xúc xắc, Hà gieo một đồng xu đều cân đối và đồng chất. Xác suất của biến cố “Con xúc xắc xuất hiện mặt 6 chấm” là

A. $\frac{1}{12}.$

B. $\frac{1}{3}.$

C. $\frac{1}{6}.$

D. $\frac{1}{2}.$

Hướng dẫn giải

Đáp án đúng là: C

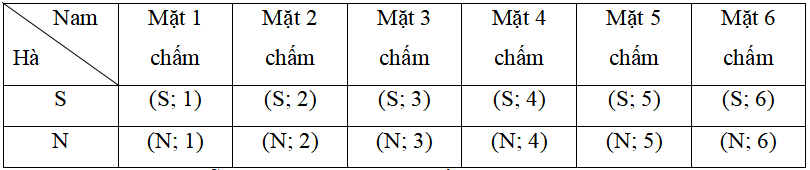
Ta có bảng sau:

Do đó, không gian mẫu của phép thử có 12 phần tử.

Kết quả thuận lợi của biến cố “Con xúc xắc xuất hiện mặt 6 chấm” là (S; 6); (N; 6).

Do đó có 2 kết quả thuận lợi cho biến cố.

Suy ra xác suất của biến cố là: $\frac{1}{6}.$

Câu 5. Bình và Minh đều có 10 tấm thẻ cùng loại được đánh số từ 1 đến 10. Hai bạn đồng thời rút ngẫu nhiên một tấm thẻ. Xác suất của biến cố “Tích chữ số trên hai tấm thẻ được rút ra là số nhỏ hơn 4” là

A. $\frac{1}{20}.$

B. $\frac{4}{100}.$

C. $\frac{4}{10}.$

D. $\frac{6}{100}.$

Hướng dẫn giải

Đáp án đúng là: A

Số phần tử của không gian mẫu là: 10.10 = 100 (phần tử).

Kết quả thuận lợi cho biến cố “Tích chữ số trên hai tấm thẻ được rút ra là số nhỏ hơn 4” là (1; 1); (1; 2); (1; 3); (2; 1); (3; 1).

Do đó, có 5 kết quả thuận lợi cho biến cố trên.

Suy ra xác suất của biến cố đó là: $\frac{5}{100}=\frac{1}{20}.$

Câu 6. Viết ngẫu nhiên một số tự nhiên lớn hơn 299 và nhỏ hơn 601. Xác suất của biến cố “Số tự nhiên được viết ra chia hết cho 9” là

A. $\frac{32}{301}.$

B. $\frac{33}{301}.$

C. $\frac{32}{300}.$

D. $\frac{33}{300}.$

Hướng dẫn giải

Đáp án đúng là: B

Ta có: Ω = {300; 301; …; 599; 600}.

Do đó, số phần tử không gian mẫu là: (600 – 300) : 1 + 1 = 301 (phần tử).

Kết quả thuận lợi của biến cố “Số tự nhiên được viết ra chi hết cho 9” là: {306; 315; …; 594}.

Do đó, số kết quả thuận lợi là: (594 – 306) : 9 + 1 = 33.

Suy ra, xác suất của biến cố “Số tự nhiên được viết ra chia hết cho 9” là: $\frac{33}{301}.$

Câu 7. Hằng gieo một con xúc xắc cân đối và đồng chất ba lần liên tiếp. Xác suất của biến cố “Ba lần gieo xuất hiện mặt có số chấm giống nhau” là

A. $\frac{1}{6}.$

B. $\frac{1}{216}.$

C. $\frac{1}{36}.$

D. $\frac{1}{72}.$

Hướng dẫn giải

Đáp án đúng là: C

Ta có số phần tử của không gian mẫu là: 6.6.6 = 216.

Kết quả thuận lợi của biến cố “Ba lần gieo xuất hiện mặt có số chấm giống nhau” là

{111; 222; 333; 444; 555; 666}.

Do đó, có 6 kết quả thuận lợi.

Suy ra, xác suất của biến cố trên là $\frac{6}{126}=\frac{1}{36}.$

Câu 8. Bạn Linh có một túi chứa các tấm thẻ như nhau được đánh số từ 5 đến 199, hai thẻ khác nhau ghi hai số khác nhau. Rút ngẫu nhiên một tấm thẻ. Xác suất của biến cố “Số trên thẻ được rút ra là số chia cho 12 và cho 30 đều dư 1” là

A. $\frac{3}{194}.$

B. $\frac{1}{97}.$

C. $\frac{2}{195}.$

D. $\frac{1}{65}.$

Hướng dẫn giải

Đáp án đúng là: D

Ta có: Ω = {5; 6;…; 199}.

Do đó, số phần tử của không gian mẫu là: (199 – 5) : 1 + 1 = 195.

Nhận thấy 12 = 2².3 và 30 = 2.3.5.

Do đó, BCNN(12; 30) = 2².3.5 = 60.

Suy ra BC(60) = {0; 60; 120; 180; 240;….}.

Từ đây, ta thấy kết quả thuận lợi của biến cố “Số trên thẻ được rút ra là số chia cho 12 và cho 30 đều dư 1” là {61; 121; 181}. Do đó, có 3 kết quả thuận lợi cho biến cố trên.

Suy ra xác suất của biến cố “Số trên thẻ được rút ra là số chia cho 12 và cho 30 đều dư 1” là $\frac{3}{195}=\frac{1}{65}.$

Câu 9. Trong một trận giao hữu của đội bóng Barcelona và Liverpool, cầu thủ Messi đã thực hiện một cú sút phạt penalty. Xác suất của biến cố “Messi sút bóng vào lưới” là

A. 1.

B. 0,5.

C. 0.

D. 0,2.

Hướng dẫn giải

Đáp án đúng là: B

Có 2 kết quả có thể xảy ra khi cầu thủ Messi thực hiện đá phạt là: đá vào lưới và đá ra ngoài.

Do đó, xác suất của biến cố “Messi sút bóng vào lưới” là: $\frac{1}{2}=0,5.$

Câu 10. Nhóm Toán của trường THCS A gồm 6 giáo viên trong đó có 4 giáo viên nam, 2 giáo viên nữ. Nhà trường muốn chọn ra hai giáo viên đi coi thi. Xác suất của biến cố “hai giáo viên đi coi thi đều là nam” là

A. $\frac{2}{3}.$

B. $\frac{2}{3}.$

C. $\frac{2}{5}.$

D. $\frac{1}{2}.$

Hướng dẫn giải

Đáp án đúng là: C

Gọi 4 giáo viên nam lần lượt là 1; 2; 3; 4.

Hai giáo viên nữ lần lượt là a, b.

Các cách chọn ra 2 giáo viên bất kì là: (1; 2); (1; 3); (1; 4); (2; 3); (3; 4); (2; 4) (1; a); (1; b); (2; a); (2; b); (3; a); (3; b); (4; a); (4; b); (a; b).

Do đó, có 15 kết quả có thể xảy ra.

Có 6 kết quả thuận lợi cho biến cố “hai giáo viên đi coi thi đều là nam” là: (1; 2); (1; 3); (1; 4); (2; 3); (2; 4); (3; 4).

Suy ra, xác suất của biến cố đó là: $\frac{6}{15}=\frac{2}{5}.$

Xem thêm các dạng bài tập Toán 9 hay, chi tiết khác:

• Tính số đo của góc nội tiếp
• Chứng minh hai góc bằng nhau dựa vào tính chất góc nội tiếp
• Chứng minh hai đường thẳng vuông góc, song song, ba điểm thẳng hàng dựa vào tính chất góc nội tiếp
• Chứng minh hai biểu thức tích bằng nhau
• Tính bán kính đường tròn ngoại tiếp và bán kính đường tròn nội tiếp của một tam giác đều

• Hơn 20.000 câu trắc nghiệm Toán,Văn, Anh lớp 9 có đáp án

---