33 câu trắc nghiệm Phương trình mũ và phương trình lôgarit có đáp án (phần 2)

---

---

Với 33 bài tập & câu hỏi trắc nghiệm Phương trình mũ và phương trình lôgarit Toán lớp 12 Giải tích có đáp án và lời giải chi tiết đầy đủ các mức độ nhận biết, thông hiểu, vận dụng sẽ giúp học sinh ôn trắc nghiệm Toán 12.

33 câu trắc nghiệm Phương trình mũ và phương trình lôgarit có đáp án (phần 2)

Câu 17: Giả sử x₁, x₂ là hai nghiệm của phương trình 7^x + 2.7^{1 - x} - 9 = 0.

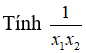
A. log₂7 + 1   B. log₇2 + 1    C. log₇2    D. log₂7

Hiển thị đáp án

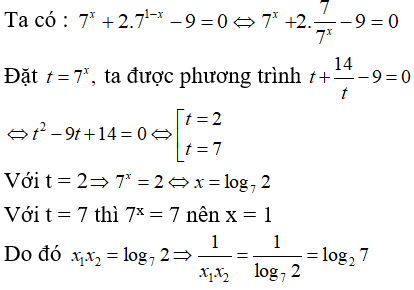
Câu 18: Tìm nghiệm của phương trình 4^{1 - x} = 3^{2x + 1}

Hiển thị đáp án

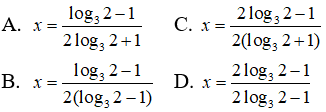
4^{1 - x} = 3^{2x + 1} ⇔ 2^{2 - 2x} = 3^{2x + 1}

Lấy lôgarit cơ số 3 hai vế ta được :

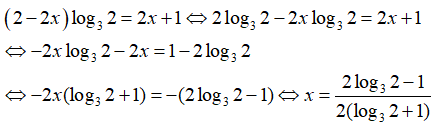
Câu 19: Giải phương trình log₅(x + 4) = 3

A. x = 11    B. x = 121    C. x = 239    D. x = 129

Hiển thị đáp án

Điều kiện : x + 4 > 0 ⇔ x > -4

PT ⇔ x + 4 = 5³ = 125 ⇔ x = 121 ( thỏa mãn điều kiện).

Vậy nghiệm cuả phương trình đã cho là 121.

Câu 20: Tìm các số thực a thỏa mãn log₁₀(a² - 15a) = 2

Hiển thị đáp án

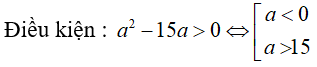
log₁₀(a² - 15a) = 2 ⇔ a² - 15a = 10² = 100 ⇔ a² - 15a - 100 = 0

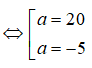
Câu 21: Giải phương trình x²lnx = lnx⁹

A. x = 3   B. x = ±3    C. x = 1, x = 3    D. x = 1, x = ±3

Hiển thị đáp án

Điều kiện x > 0.

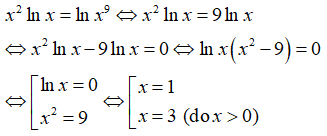
Câu 22: Giải phương trình log₄(log₃(log₂x)) = 0

A. x = 2    B. x = 8    C. x = ∛2    D. x = 4³²

Hiển thị đáp án

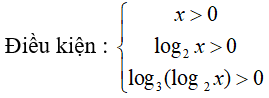
log₄(log₃(log₂x)) = 0 ⇔ log₃(log₂x) = 1 ⇔ log₂x = 3 ⇔ x = 2³ = 8 (thỏa mãn điều kiện).

Câu 23: Giải phương trình lnx + ln(x - 1) = ln2

A. x = 3/2    B. x = -1, x = 2    C. x = 2    D. x = 1, x = 3/2

Hiển thị đáp án

Điều kiện x > 1

Ta có: lnx + ln(x - 1) = ln2

⇔ x(x - 1) = 2 ⇔ x² - x - 2 = 0

⇔ x = -1 (loại) hoặc x = 2

Câu 24: Giả sử α và β là hai nghiệm của phương trình 3 + 2log₂x = log₂(14x - 3). Khẳng định nào sau đây là đúng ?

A. α = -4    B. log₂α = -2    C. α = 3/2    D. α3/14

Hiển thị đáp án

Trước hết, ta giải phương trình 3 + 2log₂x = log₂(14x - 3) (1)

Điều kiện x > 3/14. Khi đó (1) <=7gt; log₂8 + log₂x² = log₂(14x - 3)

⇔ 8x² = 14x - 3 ⇔ = 8x² - 14x + 3 = 0

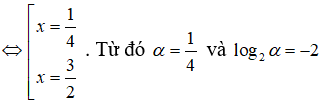
Câu 25: Tính tích các nghiệm của phương trình log_x4 + log₄x = 17/4

A. 1    B. 16    C. 4∜4   D. 256√2

Hiển thị đáp án

Điều kiện : x > 0 ; x ≠ 1

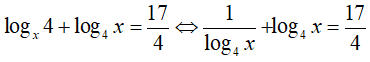
Đặt t = log₄x, nhận được phương trình:

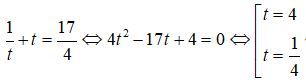
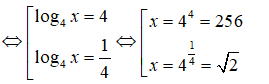
Tích hai nghiệm : 256.√2

Câu 26: Tìm hai số x và y đồng thời thỏa mãn 3^{x + y} = 81 và 81^{x - y} = 3

Hiển thị đáp án

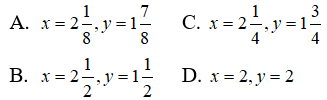
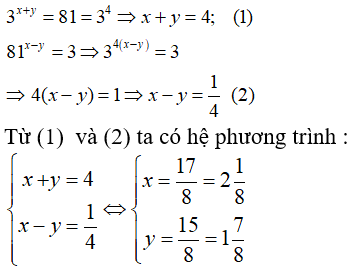
Câu 27: Một quần thể vi khuẩn bắt đầu từ 100 cá thể và cứ sau 3 giờ thì số cá thể lại tăng gấp đôi. Bởi vậy, số cá thể vi khuẩn được biểu thị theo thời gian t (tính bằng giờ) bằng công thức

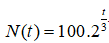
Hỏi sau bao lâu thì quần thể này đạt đến 50000 cá thể (làm tròn kết quả đến hàng phần mười) ?

A. 36,8 giờ   B. 30,2 giờ    C. 26,9 giờ    D. 18,6 giờ

Hiển thị đáp án

Sau t giờ thì số cá thể vi khuẩn có được là :

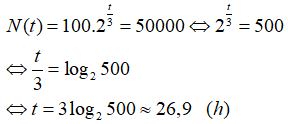
Câu 28: Khi đèn flash của một máy ảnh tắt thì ngay lập tức nguồn điện từ pin sẽ xạc cho tụ điện của nó. Lượng điện tích trong tụ xác định bởi công thức

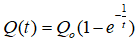
trong đó Q₀ là điện tích tối đa mà tụ có thể tích được, thời gian t tính bằng giây. Hỏi sau bao lâu thì tụ tích được 90% điện tích tối đa ?

A. 3,2 giây   B. 4,6 giây    C. 4,8 giây    D. 9,2 giây

Hiển thị đáp án

Để tụ tích được 90% điện tích tối đa thì Q(t) = 90%Q₀

Ta có: Q₀(1 - e^-1/2) = 0,9Q₀ ⇔ e^-1/2 = 0,1 ⇔ t = -2ln0,1 ≈ 4,6 (giây)

Câu 29: Chiều dài (tính bằng xentimet) của một loài cá bơn ở Thái Bình Dương theo tuổi của nó (kí hiệu là t, tính bằng năm) được ước lượng bởi công thức f(t) = 200(1 - 0,956e^-0,18t). Một con cá bơn thuộc loài này có chiều dài 140cm. Hãy ước lượng tuổi của nó.

A. 2,79 năm   B. 6,44 năm    C. 7,24 năm    D. 12,54 năm

Hiển thị đáp án

Con cá bơn có chiều dài là 140cm nên:

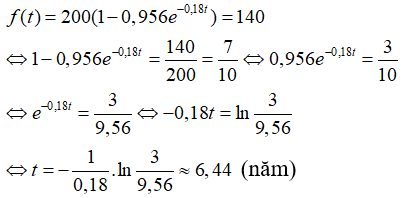
Câu 30: Có một dịch cúm trong một khu vực quân đội và số người lính ở đó mắc bệnh cúm sau t ngày (kể từ ngày dịch cúm bùng phát) được ước lượng bằng công thức

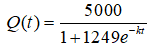
trong đó k là một hằng số. Biết rằng có 40 người lính mắc bệnh cúm sau 7 ngày. Tìm giá trị của hằng số k.

A. 0,33   B. 2,31    C. 1,31    D. -2,31

Hiển thị đáp án

Ta có:

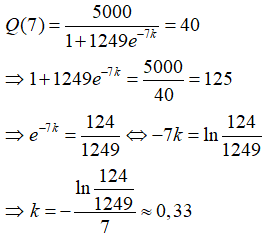
Câu 31: Nếu log(log(log(logx))) = 0 thì x = 10^k . Tìm giá trị của k

A. 10    B. 100    C. 10³    D. 10¹⁰

Hiển thị đáp án

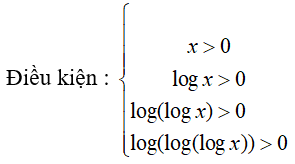
log(log(log(logx))) = 0 ⇔ log(log(logx)) = 1 ⇔ log(logx) = 10

⇔ logx = 10¹⁰ ⇔ x = 10¹⁰¹⁰ (thỏa mãn điều kiện)

⇒ k = 10¹⁰

Câu 32: Giải phương trình log₃x = (-2 + log₂100)(log₃√2)

A. x = 5    B. x = 3√2   C. x = 2⁴    D. x = 50

Hiển thị đáp án

Điều kiện : x > 0

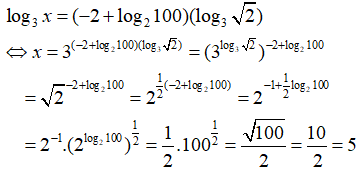
Câu 33: Tìm tập hợp các nghiệm của phương trình

Hiển thị đáp án

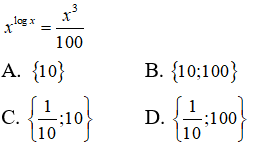
Lấy lôgarit cơ số 10 hai vế phương trình ta được

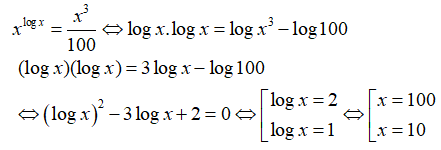
Kết hợp điều kiện, phương trình có 2 nghiệm là x= 100 và x= 10

Xem thêm Bài tập trắc nghiệm Toán 12 phần Giải tích ôn thi Tốt nghiệp THPT có đáp án hay khác:

• 30 câu trắc nghiệm Bất phương trình mũ và bất phương trình lôgarit có đáp án (phần 1)
• 30 câu trắc nghiệm Bất phương trình mũ và bất phương trình lôgarit có đáp án (phần 2)
• 40 câu trắc nghiệm Ôn tập chương 2 có đáp án
• Đề kiểm tra 1 tiết Toán 12 Giải tích Chương 2 có đáp án
• 22 câu trắc nghiệm Nguyên hàm có đáp án (phần 1)
• 22 câu trắc nghiệm Nguyên hàm có đáp án (phần 2)

---

---

---