Đề cương ôn tập Học kì 2 Toán 11 Kết nối tri thức
Bộ đề cương ôn tập Học kì 2 Toán 11 Kết nối tri thức với bài tập trắc nghiệm, tự luận đa dạng có lời giải chi tiết giúp học sinh nắm vững kiến thức cần ôn tập để đạt điểm cao trong bài thi Toán 11 Học kì 2.
Đề cương ôn tập Học kì 2 Toán 11 Kết nối tri thức
Chỉ từ 80k mua trọn bộ đề cương ôn tập Học kì 2 Toán 11 Kết nối tri thức bản word có lời giải chi tiết:
- B1: gửi phí vào tk:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án
Đề cương ôn tập Học kì 2 Toán 11 trường THPT Nguyễn Việt Hồng năm 2024-2025
Đề cương ôn tập Học kì 2 Toán 11 trường THPT Sơn Động số 3 năm 2024-2025
Đề cương ôn tập Toán 11 Học kì 2 Kết nối tri thức gồm hai phần: Nội dung ôn tập và Bài tập ôn luyện, trong đó:
- 55 bài tập trắc nghiệm;
- 7 bài tập tự luận;
I. NỘI DUNG ÔN TẬP
1. Hàm số mũ và hàm số lôgarit
Bài 18: Lũy thừa với số mũ thực
- Lũy thừa với số mũ nguyên.
- Lũy thừa với số mũ hữu tỉ.
- Lũy thừa với số mũ thực.
Bài 19: Lôgarit
- Khái niệm về lôgarit.
- Các tính chất của lôgarit.
- Lôgarit thập phân và Lôgarit tự nhiên.
Bài 20: Hàm số mũ và hàm số lôgarit
- Hàm số mũ.
- Hàm số lôgarit.
Bài 21: Phương trình và bất phương trình mũ và lôgarit
- Phương trình mũ, phương trình lôgarit.
- Bất phương trình mũ, bất phương trình lôgarit.
2. Quan hệ vuông góc trong không gian
Bài 22: Hai đường thẳng vuông góc
- Góc giữa hai đường thẳng.
- Hai đường thẳng vuông góc.
Bài 23: Đường thẳng vuông góc với mặt phẳng
- Đường thẳng vuông góc với mặt phẳng.
- Tính chất đường thẳng vuông góc với mặt phẳng.
- Liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng.
Bài 24: Phép chiếu vuông góc, góc giữa đường thẳng và mặt phẳng
- Phép chiếu vuông góc.
- Góc giữa đường thẳng và mặt phẳng.
Bài 25: Hai mặt phẳng vuông góc
- Góc giữa hai mặt phẳng.
- Hai mặt phẳng vuông góc.
- Điều kiện để hai mặt phẳng vuông góc.
- Tính chất hai mặt phẳng vuông góc.
- Góc nhị diện.
- Một số hình lăng trụ đặc biệt.
- Hình chóp đều và hình chóp cụt đều.
Bài 26: Khoảng cách
- Khoảng cách từ một điểm đến một đường thẳng, mặt phẳng.
- Khoảng cách giữa các đường thẳng và mặt phẳng song song, giữa hai mặt phẳng song song.
- Khoảng cách giữa hai đường thẳng chéo nhau.
Bài 27: Thể tích
- Thể tích khối chóp, khối chóp cụt đều, lăng trụ.
3. Các quy tắc tính xác suất
Bài 28: Biến cố hợp, biến cố giao, biến cố độc lập
- Biến cố hợp.
- Biến cố giao.
- Biến cố độc lập.
Bài 29: Công thức cộng xác suất
- Công thức cộng xác suất cho hai biến cố xung khắc.
- Công thức cộng xác suất.
Bài 30: Công thức nhân xác suất cho hai biến cố độc lập
- Công thức nhân xác suất cho hai biến cố độc lập.
4. Đạo hàm
Bài 31: Định nghĩa và ý nghĩa của đạo hàm
- Đạo hàm của hàm số tại một điểm.
- Đạo hàm của hàm số trên một khoảng.
- Các bài toán về tiếp tuyến.
Bài 32: Các quy tắc tính đạo hàm
- Đạo hàm của một số hàm số thường gặp.
- Đạo hàm của tổng, hiệu, tích, thương.
- Đạo hàm của hàm số hợp.
- Đạo hàm của hàm số lượng giác.
- Đạo hàm của hàm số mũ và lôgarit.
Bài 33: Đạo hàm cấp hai
- Khái niệm đạo hàm cấp 2.
- Ý nghĩa của đạo hàm cấp 2.
II. BÀI TẬP ÔN LUYỆN
A. TRẮC NGHIỆM
Bài 18: Lũy thừa với số mũ thực
Bài 1. Giá trị của biểu thức là
A.
B. A = 2;
C. A = 64;
D.
Bài 2. Cho . Khẳng định nào sau đây đúng?
A. a > b;
B. a < b;
C. a b;
D. a b.
Bài 3. Cho biểu thức , trong đó có dạng phân số tối giản. Gọi P = m2 + n2. Khẳng định nào sau đây đúng?
A. P (350; 360);
B. P (360; 370);
C. P (330; 340);
D. P (340; 350).
Bài 4. Cho a là một số thực dương, biểu thức bằng
A. a;
B. a3;
C. a5;
D. 1.
Bài 5. Cho số thực a thỏa mãn a3 > aπ. Mệnh đề nào sau đây đúng?
A. 0 < a < 1;
B. a < 0;
C. a > 1;
D. a = 1.
Bài 19: Lôgarit
Bài 1. Giá trị của biểu thức log425 + log21,6 bằng
A. 5;
B. 3;
C. 2;
D. 1.
Bài 2. Cho các số thực a, b dương khác 1 thỏa mãn và . Kết luận nào sau đây đúng?
A. a > 1, b > 1;
B. a > 1, 0 < b < 1;
C. 0 < a < 1, b > 1;
D. 0 < a < 1, 0 < b < 1.
Bài 3. Với a và b là hai số thực dương tùy ý, log(ab2) bằng
A. 2loga + logb;
B. loga + 2logb;
C. 2(loga + logb);
D.
Bài 4. Cho a là một số thực dương khác 1 thỏa mãn . Tính loga2.
A.
B. loga2 = 5;
C. loga2 = 20;
D.
Bài 5. Cho log2 = a; log3 = b. Tính log690 theo a, b.
A.
B.
C.
D.
Bài 20: Hàm số mũ và hàm số lôgarit
Bài 1. Tìm tập xác định D của hàm số y = log3(3 – x)
A. D = (3; +∞);
B. D = ℝ\{3};
C. D = ℝ;
D. D = (−∞; 3).
Bài 2. Một người gửi vào ngân hàng 500 triệu đồng với lãi suất 0,6% một tháng, sau mỗi tháng lãi suất được nhập vào vốn. Hỏi sau một năm người đó rút tiền thì tổng số tiền người đó nhận được là bao nhiêu?
A. 500.1,006 triệu đồng;
B. 500.1,0612 triệu đồng;
C. 500.(1 + 12.0,006)12 triệu đồng;
D. 500.1,00612 triệu đồng.
Bài 3. Trong các hàm số sau đây, hàm số nào đồng biến trên ℝ.
A.
B.
C.
D. y = 2-x.
Bài 4. Cho hai đồ thị y = ax và y = logbx có đồ thị như hình vẽ bên. Tìm khẳng định đúng.
A. 0 < a < 1; 0 < b < 1;
B. a > 1; b > 1;
C. a > 1; 0 < b < 1;
D. 0 < a < 1; b > 1.
Bài 5. Trong các hàm số sau, hàm số nào đồng biến trên ℝ.
A. y = log3x;
B.
C.
D. y = 2018x.
Bài 21: Phương trình và bất phương trình mũ và lôgarit
Bài 1. Giải bất phương trình log2(3x – 1) > 3.
A. x > 3;
B.
C. x < 3;
D.
Bài 2. Nghiệm của phương trình 22x – 1 = 2x là
A. x = 2;
B. x = −1;
C. x = 1;
D. x = −2.
Bài 3. Tích các nghiệm của phương trình bằng
A. 5;
B. 0;
C.1;
D. log65.
Bài 4. Phương trình có hai nghiệm x1;x2. Giá trị K = 2x1x2 – 3 bằng
A. 4;
B. 5;
C.6;
D. 7.
Bài 5. Tập nghiệm S của bất phương trình là
A. S = (−∞; 3];
B. S = [3; +∞);
C.S = (−∞; 1];
D. S = [1; +∞).
Bài 22: Hai đường thẳng vuông góc
Bài 1. Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Gọi I và J lần lượt là trung điểm của SC và BC. Số đo của góc (IJ, CD) bằng
A. 90°;
B. 45°;
C. 30°;
D. 60°.
Bài 2. Cho hình chóp S.ABCD có cạnh SA = x, tất cả các cạnh còn lại đều bằng a. Tính số đo của góc giữa hai đường thẳng SA và SC
A. 90°;
B. 45°;
C. 30°;
D. 60°.
Bài 3. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA (ABCD), SA = a và M là trung điểm cạnh SD. Côsin góc giữa đường thẳng AC và đường thẳng BM bằng
A.
B.
C.
D.
Bài 4. Chọn khẳng định đúng trong các khẳng định sau
A. Trong không gian hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau;
B. Trong không gian hai đường thẳng vuông góc với nhau có thể cắt nhau hoặc chéo nhau;
C. Trong không gian hai mặt phẳng cùng vuông góc với một đường thẳng thì song song với nhau;
D. Trong không gian hai đường thẳng không có điểm chung thì song song với nhau..
Bài 5. Cho hình chóp S.ABCD có đáy là hình thoi tâm O và SA = SC, SB = SD. Trong các mệnh đề sau mệnh đề nào sai?
A. AC SD;
B. BD AC;
C. BD SA;
D. AC SA.
Bài 23: Đường thẳng vuông góc với mặt phẳng
Bài 1. Cho hai đường thẳng phân biệt a, b và mặt phẳng (α). Mệnh đề nào dưới đây là đúng?
A. Nếu a (α) và b a thì b // (α);
B. Nếu a // (α) và b // (α) thì b // a;
C. Nếu a // (α) và b (α) thì a b;
D. Nếu a // (α) và b a thì b (α).
Bài 2. Cho hình chóp S.ABC có SA (ABC). Gọi H, K lần lượt là trực tâm các tam giác SBC và ABC. Mệnh đề nào sai trong các mệnh đề sau.
A. BC (SAH);
B. HK (SBC);
C. BC (SAB);
D. SH, AK và BC đồng quy.
Bài 3. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và SA (ABCD). Gọi AE, AF lần lượt là các đường cao của tam giác SAB và tam giác SAD. Khẳng định nào sau đây là đúng?
A. SC (AFB);
B. SC (AEC);
C. SC (AED);
D. SC (AEF).
Bài 4. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Gọi I, J lần lượt là trung điểm của SA và SC. Khẳng định nào dưới đây đúng?
A. IJ AB;
B. IJ AD;
C. IJ BD;
D. IJ SD.
Bài 5. Cho hình hộp ABCD.A'B'C'D' có đáy là hình thoi. Gọi O, O' lần lượt là tâm của hình bình hành ADD'A' và ABB'A'. Trong các mệnh đề sau, mệnh đề nào đúng?
A. OO' AC;
B. OO' AA';
C. OO' AD;
D. OO' AB.
Bài 24: Phép chiếu vuông góc, góc giữa đường thẳng và mặt phẳng
Bài 1. Cho hình chóp S.ABC, cạnh bên SA (ABC). Góc giữa đường thẳng SC và đáy là góc nào dưới đây?
A.
B. hoặc ;
C. ;
D.
Bài 2. Cho hình lập phương ABCD.A'B'C'D'. Xác định góc giữa đường thẳng A'C và mặt phẳng (ABCD)
A.
B.
C. hoặc ;
D. hoặc .
Bài 3. Cho hình chóp tứ giác đều S.ABCD có tất cả cạnh đều bằng a. Góc giữa đường thẳng SA và mặt phẳng (ABCD) bằng
A. 30°;
B. 60°;
C. 45°;
D. α với .
Bài 4. Cho hình lăng trụ đều ABC.A'B'C' có cạnh đáy bằng 2a, cạnh bên bằng a. Gọi M là trung điểm của BC. Tính góc giữa đường thẳng A'M và mặt phẳng đáy.
A. 30°;
B. 60°;
C. 45°;
D. 90°.
Bài 5. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính côsin góc giữa đường thẳng SB và mặt phẳng (SCD).
A.
B. cosφ = 0;
C.
D.
Bài 25: Hai mặt phẳng vuông góc
Bài 1. Cho hình chóp S.ABC có đáy ABC là tam giác đều, cạnh bên SA vuông góc với đáy, M là trung điểm AC, N là hình chiếu của B lên SC. Khẳng định nào sau đây đúng?
A. (BMN) (SBC);
B. (SAC) (SAB);
C. (BMN) (ABC);
D. (SAC) (SBC).
Bài 2. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C, mặt bên SAC là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi I là trung điểm của SC. Mệnh đề nào sau đây sai?
A. AI SC;
B. (SBC) (SAC);
C. AI BC;
D. (ABI) (SBC).
Bài 3. Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA = SC = a, . Góc giữa hai mặt phẳng (SAC) và (ABC) bằng
A. 30°;
B. 60°;
C. 45°;
D. 90°.
Bài 4. Cho hình hộp chữ nhật ABCD.A'B'C'D', BC = a, AC = 2a, . Tính góc giữa mặt phẳng (BCD'A') và mặt phẳng (ABCD).
A. 30°;
B. 60°;
C. 45°;
D. 90°.
Bài 5. Cho hình chóp đều S.ABCD có cạnh đáy bằng a, chiều cao bằng 2a. Gọi α là góc giữa mặt phẳng (SAB) và mặt phẳng (ABCD). Tính tanα.
A.
B. tanα = 1;
C. tanα = 4;
D.
Bài 26: Khoảng cách
Bài 1. Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng 2 và độ dài cạnh bên bằng 3. Khoảng cách từ S đến mặt phẳng (ABCD) bằng
A.
B. 1;
C. 7;
D.
Bài 2. Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách từ C đến mặt phẳng (BDB'D') bằng
A.
B.
C.
D.
Bài 3. Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB = a, BC = 2a, SA vuông góc với mặt phẳng đáy và SA = a. Khoảng cách giữa hai đường thẳng AC và SB bằng
A.
B.
C.
D.
Bài 4. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh , cạnh bên và SD vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng SB và CD bằng
A.
B.
C.
D. a.
Bài 5. Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D, SD (ABCD), AD = 2a, . Tính khoảng cách giữa đường thẳng CD và mặt phẳng (SAB).
A.
B.
C.
D.
Bài 27: Thể tích
Bài 1. Hình chóp S.ABCD đáy là hình chữ nhật có ; AD = 2a. Mặt bên (SAB) là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối chóp S.ABD là
A.
B.
C. 4a3;
D.
Bài 2. Cho tứ diện OABC có OA, OB, OC đôi một vuông góc và OA = OB = OC = a. Khi đó thể tích của tứ diện OABC là
A.
B.
C.
D.
Bài 3. Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A, biết AB = a, AC = 2a, A'B = 3a. Tính thể tích của khối lăng trụ ABC.A'B'C'.
A.
B.
C.
D.
Bài 4. Cho hình hộp chữ nhật ABCD.A'B'C'D', biết AB = a, BC = 2a, . Tính thể tích V của khối hộp đó.
A. 4a3;
B. 16a3;
C.
D. 8a3.
Bài 5. Cho khối lăng trụ ABC.A'B'C', tam giác A'BC có diện tích bằng 1 và khoảng cách từ A đến mặt phẳng (A'BC) bằng 2. Thể tích khối lăng trụ đã cho bằng
A. 6;
B. 3;
C. 2;
D. 1.
Bài 28: Biến cố hợp, biến cố giao, biến cố độc lập
Bài 1. Cho hai biến cố A và B. Biến cố hợp của A và B là biến cố:
A. “A và B xảy ra”;
B. “A hoặc B xảy ra”;
C. “A xảy ra”;
D. “B xảy ra hoặc cả A và B xảy ra”.
Bài 2. Tung một đồng xu cân đối và đồng chất hai lần liên tiếp. Xét các biến cố:
A: “Đồng xu xuất hiện mặt sấp ở lần gieo thứ nhất”;
B: “Đồng xu xuất hiện mặt ngửa ở lần gieo thứ hai”.
Hai biến cố A và B là hai biến cố:
A. Biến cố đối;
B. Biến cố độc lập;
C. Biến cố giao;
D. Biến cố hợp.
Bài 3. Câu lạc bộ cờ vua của một trường THPT có 20 thành viên ở ba khối, trong đó khối 10 có 3 nam và 2 nữ, khối 11 có 4 nam và 4 nữ, khối 12 có 5 nam và 2 nữ. Giáo viên chọn ngẫu nhiên một thành viên của câu lạc bộ để tham gia thi đấu giao hữu. Xét các biến cố sau:
A: “Thành viên được chọn là học sinh khối 11”;
B: “Thành viên được chọn là học sinh nam”.
Khi đó biến cố A B là:
A. “Thành viên được chọn là học sinh khối 11 và là học sinh nam”;
B. “Thành viên được chọn là học sinh khối 11 và không là học sinh nam”;
C. “Thành viên được chọn là học sinh khối 11 hoặc là học sinh nam”;
D. “Thành viên được chọn không là học sinh khối 11 hoặc là học sinh nam”.
Bài 4. Chọn ngẫu nhiên một số tự nhiên từ 1 đến 20. Xét các biến cố A: “Số được chọn chia hết cho 3”, B: “Số được chọn chia hết cho 4”. Khi đó biến cố A B là
A. {3; 4; 12};
B. {3; 4; 6; 8; 9; 12; 15; 16; 18; 20};
C. {12};
D. {3; 6; 9; 12; 15; 18}.
Bài 5. Hai xạ thủ tham gia thi đấu bắn súng, mỗi người bắn vào bia của mình một viên đạn một cách độc lập với nhau. Gọi A và B lần lượt là các biến cố “Người thứ nhất bắn trúng bia”; “Người thứ hai bắn trúng bia”. Khẳng định nào sau đây đúng?
A. Hai biến cố A và B bằng nhau;
B. Hai biến cố A và B đối nhau;
C. Hai biến cố A và B độc lập với nhau;
D. Hai biến cố A và B không độc lập với nhau.
................................
................................
................................
B. TỰ LUẬN
Bài 1. Tính
a) log400 – log 4.
b)
c) log45.log56.log68.
Bài 2. Biết rằng khi độ cao tăng lên, áp suất không khí sẽ giảm và công thức áp suất dựa trên độ cao là a = 15500.(5 - logp) trong đó a là độ cao so với mực nước biển (tính bằng mét) và p là áp suất không khí (tính bằng pascal). Tính áp suất không khí ở đỉnh Everest có độ cao 8850 m so với mực nước biển.
Bài 3. Vẽ các đồ thị các hàm số sau
a) y = 3x.
b) ơ
Bài 4. Tìm tập xác định của các hàm số sau:
a) y = log|x + 3|.
b) y = 12x.
c) y = log5(2x – 3).
Bài 5. Giải các phương trình sau
a) 2.10x = 30.
b) 42x = 82x – 1.
c) 5x = 32x – 1.
Bài 6. Giải các phương trình sau
a) 2log4x + log2(x – 3) = 2.
b) log3(x2 – 3x + 2) = log3(2x – 4).
Bài 7. Giải các bất phương trình sau
a) 2.52x + 1 3.
b) log3(x + 7) −1.
c) log0,5(x + 7) log0,5(2x – 1).
................................
................................
................................
Xem thêm đề cương ôn tập Toán 11 Kết nối tri thức có lời giải hay khác:
Để học tốt lớp 11 các môn học sách mới:
- Giải bài tập Lớp 11 Kết nối tri thức
- Giải bài tập Lớp 11 Chân trời sáng tạo
- Giải bài tập Lớp 11 Cánh diều
Tủ sách VIETJACK shopee lớp 10-11 (cả 3 bộ sách):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giáo án lớp 11 (các môn học)
- Giáo án điện tử lớp 11 (các môn học)
- Giáo án Toán 11
- Giáo án Ngữ văn 11
- Giáo án Tiếng Anh 11
- Giáo án Vật Lí 11
- Giáo án Hóa học 11
- Giáo án Sinh học 11
- Giáo án Lịch Sử 11
- Giáo án Địa Lí 11
- Giáo án KTPL 11
- Giáo án HĐTN 11
- Giáo án Tin học 11
- Giáo án Công nghệ 11
- Giáo án GDQP 11
- Đề thi lớp 11 (các môn học)
- Đề thi Ngữ Văn 11 (có đáp án)
- Chuyên đề Tiếng Việt lớp 11
- Đề cương ôn tập Văn 11
- Đề thi Toán 11 (có đáp án)
- Đề thi Toán 11 cấu trúc mới
- Đề cương ôn tập Toán 11
- Đề thi Tiếng Anh 11 (có đáp án)
- Đề thi Tiếng Anh 11 mới (có đáp án)
- Đề thi Vật Lí 11 (có đáp án)
- Đề thi Hóa học 11 (có đáp án)
- Đề thi Sinh học 11 (có đáp án)
- Đề thi Lịch Sử 11
- Đề thi Địa Lí 11 (có đáp án)
- Đề thi KTPL 11
- Đề thi Tin học 11 (có đáp án)
- Đề thi Công nghệ 11
- Đề thi GDQP 11 (có đáp án)

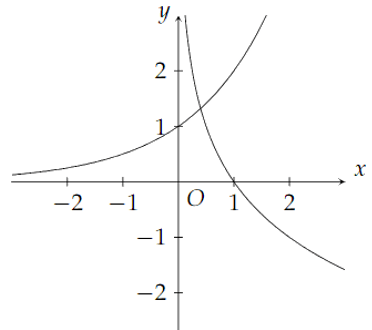



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

