(Ôn thi ĐGNL, ĐGTD) Chuyên đề: Đại số
Chuyên đề Đại số trong tài liệu ôn thi Đánh giá năng lực, Đánh giá tư duy theo cấu trúc mới nhất đầy đủ lý thuyết trọng tâm, các dạng bài & bài tập đa dạng từ cơ bản đến nâng cao giúp Giáo viên & học sinh có thêm tài liệu ôn thi ĐGNL HSA, VACT và ĐGTD TSA đạt kết quả cao.
(Ôn thi ĐGNL, ĐGTD) Chuyên đề: Đại số
Xem thử Tài liệu & Đề thi HSA Xem thử Tài liệu & Đề thi VACT Xem thử Tài liệu & Đề thi TSA Xem thử Tài liệu & Đề thi SPT
Chỉ từ 200k mua trọn bộ Đề thi & Tài liệu ôn thi ĐGNL - ĐGTD năm 2026 của các trường theo cấu trúc mới bản word có lời giải chi tiết:
- B1: gửi phí vào tk:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận đề thi
A. TÓM TẮT KIẾN THỨC NỀN TẢNG
Biểu thức đại số |
Một số lưu ý và ví dụ |
Biểu thức đại số |
• Nhận biết biểu thức: số, đại số. • Tính giá trị của biểu thức đại số. |
Đa thức (một biến và nhiều biến) |
• Tìm bậc, tìm hệ số cao nhất, hệ số tự do, tổng các hệ số của một đa thức một biến. • Tìm bậc của một đa thức nhiều biến. • Nhận biết, tìm điều kiện về nghiệm của đa thức một biến, nhiều biến. • Thực hiện phép cộng, phép trừ, phép nhân hai đa thức. • Phép chia đa thức, phép chia có dư và sự chia hết. • Phân tích đa thức thành nhân tử. |
Hằng đẳng thức |
• Áp dụng bảy hằng đẳng thức đáng nhớ. • Sử dụng hằng đẳng thức để phân tích đa thức thành nhân tử. • Ứng dụng hằng đẳng thức để chứng minh bất đẳng thức, tìm giá trị lớn nhất, giá trị nhỏ nhất của một biểu thức. • Ứng dụng hằng đẳng thức trong các bài toán về số học. Ví dụ: Tìm số nguyên dương n sao cho n20 + n10 + 1 là một số nguyên tố. • Ứng dụng hằng đẳng thức trong các bài toán về đa thức, v.v. |
Phân thức đại số |
• Nhận biết các khái niệm cơ bản của phân thức đại số. • Thực hiện các phép toán về các phân thức đại số. |
Căn thức |
Một số lưu ý và ví dụ |
Căn bậc n của số thực |
• Nhận biết căn bậc hai (tổng quát: căn bậc chẵn) của một số thực không âm, căn bậc ba (tổng quát: căn bậc lẻ) của một số thực. • Thực hiện các phép toán về căn thức, biến đổi căn thức. |
Căn thức bậc n của biểu thức đại số |
• Nhận biết căn bậc n của một biểu thức đại số. • Thực hiện một số phép biến đổi đơn giản về căn thức bậc n của biểu thức đại số. Ví dụ: Biến đổi căn thức bậc hai của một bình phương, căn thức bậc hai của một tích, căn thức bậc hai của một thương, trục căn thức ở mẫu. |
Hàm số và đồ thị |
Một số lưu ý và ví dụ |
Đại cương về hàm số và đồ thị |
• Nhận biết những mô hình thực tế dẫn đến khái niệm hàm số. • Tính giá trị của hàm số khi hàm số đó xác định bởi công thức. • Xác định tọa độ của một điểm trên mặt phẳng tọa độ; xác định một điểm trên mặt phẳng tọa độ khi biết tọa độ của nó. • Nhận biết đồ thị hàm số. Ví dụ: Nhận ra đường thẳng là đồ thị của một hàm số, đường tròn không phải là đồ thị của một hàm số. • Nhận biết các khái niệm về hàm số chẵn, hàm số lẻ, hàm số tuần hoàn. • Nhận biết các đặc trưng hình học của đồ thị hàm số chẵn, hàm số lẻ, hàm số tuần hoàn. |
Hàm số và đồ thị bậc nhất |
• Thiết lập bảng giá trị của hàm số bậc nhất. • Đồ thị của hàm số bậc nhất. • Nhận biết khái niệm hệ số góc của đường thẳng. • Sử dụng hệ số góc của đường thẳng để nhận biết và giải thích được sự cắt nhau hoặc song song của hai đường thẳng cho trước. • Vận dụng hàm số bậc nhất và đồ thị vào giải quyết một số bài toán thực tiễn. Ví dụ: Bài toán về chuyển động đều trong Vật lý. |
Hàm số và đồ thị bậc hai |
• Thiết lập bảng giá trị của hàm số bậc hai. • Lập bảng biến thiên, vẽ đồ thị của hàm số bậc hai. • Nhận biết tính đối xứng (trục) và trục đối xứng của đồ thị hàm số. • Giải quyết một số vấn đề thực tiễn gắn với hàm số và đồ thị. Ví dụ: Các bài toán liên quan đến chuyển động trong Vật lý. |
Phương trình và hệ phương trình |
Một số lưu ý và ví dụ |
Phương trình bậc nhất một ẩn, hai ẩn |
• Phương trình bậc nhất một ẩn và cách giải. Giải quyết một số vấn đề thực tiễn gắn với phương trình bậc nhất. Ví dụ: Các bài toán liên quan đến chuyển động trong Vật lý, các bài toán liên quan đến Hóa học. • Giải phương trình có dạng tích, phương trình chứa ẩn ở mẫu quy về phương trình bậc nhất. • Nhận biết khái niệm phương trình bậc nhất hai ẩn, nghiệm và biểu diễn tập hợp nghiệm của phương trình bậc nhất hai ẩn. |
Hệ phương trình bậc nhất hai ẩn, ba ẩn |
• Nhận biết khái niệm, nghiệm và cách giải hệ hai phương trình bậc nhất hai ẩn, hệ ba phương trình bậc nhất ba ẩn. • Giải quyết một số vấn đề thực tiễn gắn với hệ hai phương trình bậc nhất hai ẩn. Ví dụ: Các bài toán liên quan đến cân bằng phản ứng trong Hóa học. • Vận dụng cách giải hệ phương trình bậc nhất ba ẩn vào giải quyết một số bài toán Vật lý, Hóa học, v.v. và giải quyết một số vấn đề thực tiễn cuộc sống. Ví dụ: Trong Vật lý (tính điện trở, tính cường độ dòng điện trong dòng điện không đổi); trong Hóa học (cân bằng phản ứng, v.v.); trong Sinh học (bài tập nguyên phân, giảm phân, v.v.); trong thực tiễn (bài toán lập kế hoạch sản xuất, mô hình cân bằng thị trường, phân bổ vốn đầu tư, v.v.). |
Phương trình bậc hai một ẩn. Định lý Viète |
• Nhận biết khái niệm phương trình bậc hai một ẩn. Giải phương trình bậc hai một ẩn. • Giải phương trình quy về phương trình bậc hai. • Áp dụng định lý Viète và ứng dụng của nó. Ví dụ: Tính nhẩm nghiệm của phương trình bậc hai, tìm hai số biết tổng và tích của chúng, biểu thức đối xứng giữa hai nghiệm. • Vận dụng phương trình bậc hai vào giải quyết bài toán thực tiễn. |
Bất đẳng thức. Bất phương trình, hệ bất phương trình |
Một số lưu ý và ví dụ |
Bất đẳng thức |
• Nhận biết thứ tự trên tập hợp các số thực. • Nhận biết bất đẳng thức và mô tả được một số tính chất cơ bản của bất đẳng thức (tính chất bắc cầu; liên hệ giữa thứ tự và phép cộng, phép nhân). • Áp dụng một số bất đẳng thức, chẳng hạn như bất đẳng thức Cauchy, bất đẳng thức tam giác, v.v. để chứng minh bất đẳng thức, tìm giá trị lớn nhất, giá trị nhỏ nhất của một biểu thức. |
Bất phương trình bậc nhất một ẩn |
• Nhận biết khái niệm bất phương trình bậc nhất một ẩn, nghiệm của bất phương trình bậc nhất một ẩn. • Giải bất phương trình bậc nhất một ẩn. |
Dấu của tam thức bậc hai. Bất phương trình bậc hai một ẩn |
• Giải thích định lý về dấu của tam thức bậc hai từ việc quan sát đồ thị của hàm số bậc hai. • Giải bất phương trình bậc hai. • Vận dụng bất phương trình bậc hai một ẩn vào giải quyết bài toán thực tiễn. Ví dụ: Xác định chiều cao tối đa để xe có thể qua hầm có hình dạng Parabol. |
Bất phương trình và hệ bất phương trình bậc nhất hai ẩn |
• Nhận biết bất phương trình và hệ bất phương trình bậc nhất hai ẩn. • Biểu diễn miền nghiệm của bất phương trình và hệ bất phương trình bậc nhất hai ẩn trên mặt phẳng tọa độ. • Vận dụng kiến thức về bất phương trình, hệ bất phương trình bậc nhất hai ẩn vào giải quyết bài toán thực tiễn. Ví dụ: Bài toán tìm cực trị của biểu thức F = ax + by trên một miền đa giác. • Vận dụng các kiến thức về hệ bất phương trình bậc nhất để giải quyết một số bài toán quy hoạch tuyến tính. |
Tập hợp. Mệnh đề |
Một số lưu ý và ví dụ |
Mệnh đề |
• Thiết lập và phát biểu được các mệnh đề toán học, bao gồm: mệnh đề phủ định; mệnh đề đảo; mệnh đề tương đương; mệnh đề có chứa ký hiệu ; điều kiện cần, điều kiện đủ, điều kiện cần và đủ. • Xác định được tính đúng/sai của một mệnh đề toán học trong những trường hợp đơn giản. |
Tập hợp |
• Nhận biết các khái niệm cơ bản về tập hợp (tập con, hai tập hợp bằng nhau, tập rỗng) và biết sử dụng các ký hiệu • Thực hiện các phép toán trên các tập hợp (hợp, giao, hiệu của hai tập hợp, phần bù của một tập con) và biết dùng biểu đồ Ven để biểu diễn chúng trong những trường hợp cụ thể. • Giải quyết một số vấn đề thực tiễn gắn với phép toán trên tập hợp. Ví dụ: Những bài toán liên quan đến đếm số phần tử của hợp các tập hợp. |
Đại số tổ hợp |
Một số lưu ý và ví dụ |
Các quy tắc đếm (quy tắc cộng, quy tắc nhân, chỉnh hợp, hoán vị, tổ hợp) và ứng dụng trong thực tiễn |
• Vận dụng quy tắc cộng và quy tắc nhân trong một số tình huống đơn giản. Ví dụ: Đếm số khả năng xuất hiện mặt sấp/ngửa khi tung một số đồng xu. • Vận dụng sơ đồ hình cây trong các bài toán đếm đơn giản các đối tượng trong Toán học, trong các môn học khác cũng như trong thực tiễn. Ví dụ: Đếm số hợp từ tạo thành trong Sinh học, hoặc đếm số trận đấu trong một giải thể thao. • Tính số các hoán vị, chỉnh hợp, tổ hợp và ứng dụng. |
Nhị thức Newton |
• Khai triển nhị thức Newton (a + b)n với số mũ thấp (n = 4 hoặc n = 5) bằng cách sử dụng tam giác Pascal. • Khai triển nhị thức Newton (a + b)n bằng cách vận dụng tổ hợp. • Xác định hệ số trong khai triển của một biểu thức; sử dụng khai triển nhị thức Newton để rút gọn hoặc chứng minh các biểu thức liên quan đến tổ hợp. Ví dụ: Tìm hệ số tự do trong khai triển của biểu thức với x > 0. |
................................
................................
................................
B. MỘT SỐ VÍ DỤ
Ví dụ 1. Cho mệnh đề . Mệnh đề phủ định của mệnh đề P là:
A.
B.
C.
D.
Hướng dẫn giải
Đáp án: C.
Để xác định mệnh đề phủ định của P, ta thay ký hiệu bởi ký hiệu và lấy phủ định của phát biểu "n2 + 1 > 2". Vậy mệnh đề là:
Ví dụ 2. Khi một vật ở độ cao y0 (so với mặt đất) được ném xiên lên cao theo vật này là góc α (so với phương ngang) với vận tốc ban đầu v0 (m/s) thì phương trình chuyển động của vật này là
ở đây lấy g = 9,8 m/s2 là gia tốc trọng trường, x là khoảng cách theo phương ngang của vật so với vị trí ban đầu.
Một vận động viên ném lao đã lập kỷ lục cá nhân với độ xa 104 m. Biết người này ném lao từ độ cao 1,8 m và góc ném là 45°. Hỏi vận tốc ban đầu của lao khi được ném đi xấp xỉ là bao nhiêu (làm tròn đến phần chục)?
A. 31,7 (m/s).
B. 31,6 (m/s).
C. 29,6 (m/s).
D. 29,5 (m/s).
Hướng dẫn giải
Đáp án: A.
Khi góc ném bằng 45° và lao được ném từ độ cao 1,8 m, ta có
Độ xa x = 104 ứng với y = 0, nghĩa là
Ví dụ 3. Biết rằng, số chia hết cho 11 khi và chỉ khi a – b + c − d chia hết cho 11. Có thể lập được bao nhiêu số gồm 4 chữ số khác nhau, chia hết cho 11 và tổng các chữ số của nó bằng 18?
A. 72.
B. 80.
C. 36.
D. 90.
Hướng dẫn giải
Đáp án: A.
Gọi là một số bất kỳ thỏa mãn bài toán.
Khi đó, ta có a – b + c − d chia hết cho 11 (1) và a + b + c + d = 18 (2).
Ta có (a + c) + (b + d) = 18 là một số chẵn, suy ra a + c và b + dcùng tính chẵn, lẻ.
Do đó, a – b + c – d là một số chẵn.
Mặt khác, ta có a, b, c, d phân biệt nên −16 ≤ a – b + c – d ≤ 16. Kết hợp với (1), ta suy ra a – b + c – d = 0 (3).
Từ (2) và (3) ta suy ra a + c = b + d = 9.
Vì a khác 0 nên a có 9 cách chọn. Khi đó, do c = 9 – a ≠ a nên c có 1 cách chọn.
Tiếp theo, do b khác a và khác c nên b còn 8 cách chọn.
Cuối cùng, do d = 9 – b ≠ b, a, c nên d còn 1 cách chọn.
Vậy có tất cả 9 ∙ 1 ∙ 8 ∙ 1 = 72 số thỏa mãn bài toán.
Ví dụ 4. Cho a, b là hai số nguyên. Mỗi phát biểu sau là đúng hay sai?
STT |
Phát biểu |
Đúng |
Sai |
1 |
|||
2 |
Nếu a = b + 3 thì a3 – b3 chia hết cho 9. |
Hướng dẫn giải
Đáp án: 1) Đúng; 2) Đúng.
Ta có
Khi a, b là các số nguyên thỏa mãn a = b + 3, ta có
chia hết cho 9.
Ví dụ 5. Bạn An được mẹ giao nấu ăn cho gia đình trong ngày thứ Bảy tuần sau. Mẹ bạn An cho biết, gia đình bạn An cần ít nhất 900 g chất protein và 400 g chất lipid trong thức ăn mỗi ngày. Để cần đủ lượng chất protein và lipid cho gia đình, bạn An dự định mua hai loại thịt bò và thịt lợn. Trong một ngày, nhà bạn An chỉ ăn nhiều nhất 1600 g thịt bò, 1100 g thịt lợn. Biết rằng thịt bò chứa 80% protein và 20% lipid. Thịt lợn chứa 60% protein và 40% lipid. Giá tiền 1 kg thịt bò là 135 000 đồng, 1 kg thịt lợn là 105 000 đồng. Giả sử bạn An mua x (kg) thịt bò và y (kg) thịt lợn. Gọi T (nghìn đồng) là số tiền An phải trả cho x (kg) thịt bò và y (kg) thịt lợn. Mỗi phát biểu sau là đúng hay sai?
STT |
Phát biểu |
Đúng |
Sai |
1 |
8x + 6y ≥ 9 |
||
2 |
Miền nghiệm biểu diễn các cặp (x; y) là miền trong của một tam giác. |
||
3 |
Số tiền tối thiểu bạn An cần trả cho phần thịt bò và thịt lợn trong ngày thứ Bảy tuần sau là 156 000 đồng. |
Hướng dẫn giải
Đáp án: 1) Đúng; 2) Sai; 3) Sai.
1) Từ giả thiết của bài toán, trong một ngày gia đình bạn An cần ít nhất 900 g chất protein. Trong 1 kg thịt bò chứa 80% protein và 1 kg thịt lợn chứa 60% protein, nên ta suy ra: 0,8x + 0,6y ≥ 0,9, nghĩa là 8x + 6y ≥ 9.
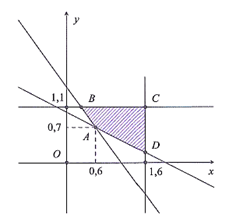
2) Từ giả thiết, ta có hệ bất phương trình
và miền nghiệm của hệ trên được biểu diễn là miền trong của tứ giác ABCD với A(0,6; 0,7); B(0,3; 1,1), C(1,6; 1,1) và D(1,6; 0,2).
3) Chi phí mua thịt bò và thịt lợn là T(x; y) = 135x + 105y (nghìn đồng), Hàm T(x; y) đạt giá trị nhỏ nhất khi (x; y) là tọa độ của một trong các đỉnh A, B, C, D. Ta có:
T (0,6; 0,7) = 135 ∙ 0,6 + 105 ∙ 0,7 = 154,5
T (0,3; 1,1) = 135 ∙ 0,3 + 105 ∙ 1,1=156
T (1,6; 1,1) = 135 ∙ 1,6 + 105 ∙ 1,1 = 331,5
T (1,6; 0,2) = 135 ∙ 1,6 + 105 ∙ 0,2 = 237.
Vậy T đạt giá trị nhỏ nhất bằng 154,5 nghìn đồng khi (x; y) = (0,6; 0,7), nghĩa là số tiền tối thiểu bạn An cần trả để mua thịt bò và thịt lợn trong ngày thứ Bảy tuần sau là 154 500 đồng.
................................
................................
................................
C. BÀI TẬP TỰ LUYỆN
Bài 1. Gọi X là tập hợp các học sinh của lớp 10A. Gọi I là tập hợp các học sinh của lớp 10A biết chơi cờ vua, gọi T là tập hợp các học sinh của lớp 10A biết chơi cờ tướng Khẳng định nào dưới đây là đúng cho tập hợp ?
A. Y là tập hợp các học sinh của lớp 10A không biết chơi cờ vua nhưng biết chơi cờ tướng.
B. Y là tập hợp các học sinh của lớp 10A không biết chơi cả hai môn cờ vua và cờ tướng.
C. Y là tập hợp các học sinh của lớp 10A biết chơi cờ vua hoặc cờ tướng.
D. Y là tập hợp các học sinh của lớp 10A biết chơi cả hai môn cờ vua và cờ tướng.
Bài 2. Một vật thả tự do từ độ cao 200 m, sau khoảng thời gian t (giây) vật cách mặt đất một khoảng h(t) = 200 – 5t2 (m). Hỏi trong những khoảng thời gian nào dưới đây, vật cách mặt đất với độ cao lớn hơn 20 m?
A.
B.
C.
D.
Bài 3. Trong các số tự nhiên từ 1 đến 100 000, có bao nhiêu số mà trong mỗi số đó có ít nhất hai chữ số 5?
A. 8 145.
B. 34 389.
C. 7 290.
D. 8 146.
Bài 4. Khai triển thành đa thức
Mỗi phát biểu sau đúng hay sai?
STT |
Phát biểu |
Đúng |
Sai |
1 |
a0 = 1. |
||
2 |
a5 = 32. |
||
3 |
a2 = −40. |
Bài 5. Với mỗi số nguyên dương n, gọi là tập hợp các số nguyên chia hết cho n. Mỗi phát biểu sau đúng hay sai?
STT |
Phát biểu |
Đúng |
Sai |
1 |
là tập hợp các số nguyên chẵn. |
||
2 |
|||
3 |
................................
................................
................................
Xem thử Tài liệu & Đề thi HSA Xem thử Tài liệu & Đề thi VACT Xem thử Tài liệu & Đề thi TSA Xem thử Tài liệu & Đề thi SPT
Xem thêm tài liệu ôn thi đánh giá năng lực HSA, VACT, đánh giá tư duy TSA hay khác:
- (Ôn thi ĐGTD TSA) Chuyên đề: Số học
- (Ôn thi ĐGTD TSA) Chuyên đề: Giải tích
- (Ôn thi ĐGTD TSA) Chuyên đề: Hình học và đo lường
- (Ôn thi ĐGTD TSA) Chuyên đề: Xác suất và thống kê
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 12 Global Success
- Giải sgk Tiếng Anh 12 Smart World
- Giải sgk Tiếng Anh 12 Friends Global
- Lớp 12 Kết nối tri thức
- Soạn văn 12 (hay nhất) - KNTT
- Soạn văn 12 (ngắn nhất) - KNTT
- Giải sgk Toán 12 - KNTT
- Giải sgk Vật Lí 12 - KNTT
- Giải sgk Hóa học 12 - KNTT
- Giải sgk Sinh học 12 - KNTT
- Giải sgk Lịch Sử 12 - KNTT
- Giải sgk Địa Lí 12 - KNTT
- Giải sgk Giáo dục KTPL 12 - KNTT
- Giải sgk Tin học 12 - KNTT
- Giải sgk Công nghệ 12 - KNTT
- Giải sgk Hoạt động trải nghiệm 12 - KNTT
- Giải sgk Giáo dục quốc phòng 12 - KNTT
- Giải sgk Âm nhạc 12 - KNTT
- Giải sgk Mĩ thuật 12 - KNTT
- Lớp 12 Chân trời sáng tạo
- Soạn văn 12 (hay nhất) - CTST
- Soạn văn 12 (ngắn nhất) - CTST
- Giải sgk Toán 12 - CTST
- Giải sgk Vật Lí 12 - CTST
- Giải sgk Hóa học 12 - CTST
- Giải sgk Sinh học 12 - CTST
- Giải sgk Lịch Sử 12 - CTST
- Giải sgk Địa Lí 12 - CTST
- Giải sgk Giáo dục KTPL 12 - CTST
- Giải sgk Tin học 12 - CTST
- Giải sgk Hoạt động trải nghiệm 12 - CTST
- Giải sgk Âm nhạc 12 - CTST
- Lớp 12 Cánh diều
- Soạn văn 12 Cánh diều (hay nhất)
- Soạn văn 12 Cánh diều (ngắn nhất)
- Giải sgk Toán 12 Cánh diều
- Giải sgk Vật Lí 12 - Cánh diều
- Giải sgk Hóa học 12 - Cánh diều
- Giải sgk Sinh học 12 - Cánh diều
- Giải sgk Lịch Sử 12 - Cánh diều
- Giải sgk Địa Lí 12 - Cánh diều
- Giải sgk Giáo dục KTPL 12 - Cánh diều
- Giải sgk Tin học 12 - Cánh diều
- Giải sgk Công nghệ 12 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 12 - Cánh diều
- Giải sgk Giáo dục quốc phòng 12 - Cánh diều
- Giải sgk Âm nhạc 12 - Cánh diều

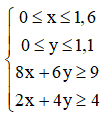



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

