(Ôn thi ĐGNL, ĐGTD) Chuyên đề: Giải tích
Chuyên đề Giải tích trong tài liệu ôn thi Đánh giá năng lực, Đánh giá tư duy theo cấu trúc mới nhất đầy đủ lý thuyết trọng tâm, các dạng bài & bài tập đa dạng từ cơ bản đến nâng cao giúp Giáo viên & học sinh có thêm tài liệu ôn thi ĐGNL HSA, VACT và ĐGTD TSA đạt kết quả cao.
(Ôn thi ĐGNL, ĐGTD) Chuyên đề: Giải tích
Xem thử Tài liệu & Đề thi HSA Xem thử Tài liệu & Đề thi VACT Xem thử Tài liệu & Đề thi TSA Xem thử Tài liệu & Đề thi SPT
Chỉ từ 200k mua trọn bộ Đề thi & Tài liệu ôn thi ĐGNL - ĐGTD năm 2026 của các trường theo cấu trúc mới bản word có lời giải chi tiết:
- B1: gửi phí vào tk:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận đề thi
A. TÓM TẮT KIẾN THỨC NỀN TẢNG
Giới hạn. Hàm số liên tục |
Một số lưu ý và ví dụ |
Giới hạn của dãy số. Phép toán giới hạn dãy số. Tổng của một cấp số nhân lùi vô hạn |
• Xác định giới hạn của một số dãy số quen thuộc. Ví dụ: • Vận dụng các quy tắc để tìm giới hạn của dãy số. Ví dụ: • Vận dụng kết quả về tổng cấp số nhân lùi vô hạn vào trong một số tình huống thực tiễn. Ví dụ: Đổi số thập phân vô hạn tuần hoàn sang phân số. |
Giới hạn của hàm số. Phép toán giới hạn hàm số |
• Xác định giới hạn tại một điểm, tại vô cực và giới hạn một phía của các hàm số. Ví dụ: • Vận dụng các quy tắc để tìm giới hạn của hàm số. Ví dụ: • Giải quyết một số vấn đề thực tiễn gắn với giới hạn hàm số. Ví dụ: Tính “điểm bão hòa”, v.v.. |
Hàm số liên tục |
• Nhận dạng hàm số liên tục tại một điểm, hoặc trên một khoảng, hoặc trên một đoạn. • Áp dụng các công thức, vận dụng để xét tính liên tục của hàm số là kết quả của các phép toán sơ cấp giữa các hàm số quen thuộc. Ví dụ: • Phân tích và tổng hợp các tình huống xảy ra về tính liên tục của hàm số trong một số tình huống cụ thể. Ví dụ: Xác định các tham số phù hợp để hàm số liên tục tại một điểm, v.v.. |
Đạo hàm |
Một số lưu ý và ví dụ |
Khái niệm đạo hàm. Ý nghĩa hình học của đạo hàm |
• Nhận biết được khái niệm vận tốc tức thời. • Tính được đạo hàm của hàm số tại một điểm bằng định nghĩa. Ví dụ: Tính f'(3) với f(x) = x2. • Nhận biết ý nghĩa hình học của đạo hàm. • Thiết lập phương trình tiếp tuyến của đồ thị hàm số tại một điểm; phương trình tiếp tuyến của đồ thị thỏa mãn một số điều kiện cho trước. Ví dụ: Viết phương trình tiếp tuyến của đồ thị y = x2 song song với đường thẳng y = x, v.v.. |
Các quy tắc tính đạo hàm |
• Tính đạo hàm của một số hàm thông dụng (như hàm đa thức, căn thức, hàm số lượng giác, hàm số mũ, hàm số lôgarit). • Áp dụng các công thức tính đạo hàm của tổng, hiệu, tích, thương của các hàm số và đạo hàm của hàm hợp. Ví dụ: • Giải quyết một số vấn đề liên môn hoặc vấn đề gắn với thực tiễn. Ví dụ: Xác định vận tốc tức thời của chuyển động, biên lợi nhuận, v.v.. |
Đạo hàm cấp hai |
• Tính đạo hàm cấp hai của một số hàm thông dụng (như hàm đa thức, hàm lũy thừa, hàm số lượng giác, hàm số mũ, hàm số lôgarit). • Giải quyết một số vấn đề có liên quan đến môn học khác hoặc bài toán có yếu tố thực tiễn. Ví dụ: Xác định gia tốc của chuyển động, v.v.. |
Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số |
Một số lưu ý và ví dụ |
Tính đơn điệu của hàm số |
• Nhận biết tính đơn điệu, cực trị của hàm số dựa vào việc xác định dấu của đạo hàm. • Xác định các khoảng đồng biến, nghịch biến, các điểm cực trị của các hàm số thông dụng và thể hiện được các tính chất này trên bảng biến thiên. • Thiết lập các điều kiện cần thiết để hàm số đơn điệu trên khoảng cho trước. Ví dụ: đồng biến trên từng khoảng xác định; v.v.. • Thông qua lập luận để phát hiện các tính chất đặc biệt của cực trị hàm số. Ví dụ: Nếu F'(x) liên tục thì các điểm cực trị là nghiệm của F'(x); v.v.. |
Giá trị lớn nhất, giá trị nhỏ nhất của hàm số |
• Thông qua bảng biến thiên, đồ thị hàm số, xác định các giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một tập xác định cho trước. • Vận dụng các tính chất về sự đơn điệu của hàm số để tìm các cụ the. giá trị lớn nhất, giá trị nhỏ nhất của các hàm số Ví dụ: Tìm GTLN, GTNN của hàm số
|
Khảo sát và vẽ đồ thị của hàm số |
• Nhận biết các đường tiệm cận của đồ thị hàm số. Ví dụ: • Kết hợp các tính chất của hàm số để phác họa đồ thị của các hàm số quen thuộc. Ví dụ: y = ax3 + bx2 + cx + d. • Vận dụng và phát hiện các tính chất đặc biệt của đồ thị, tính tương giao giữa các đồ thị hàm số quen thuộc. Ví dụ: Tích các khoảng cách giữa một điểm trên đồ thị tới hai tiệm cận là không đổi. |
Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn |
• Vận dụng các tính chất của hàm số và đồ thị hàm số để giải quyết một số vấn đề liên quan đến thực tiễn. Ví dụ: Cực đại hóa lợi nhuận, cực tiểu hóa chi phí, v.v.. |
|
Nguyên hàm. Tích phân |
Một số lưu ý và ví dụ |
Nguyên hàm. Bảng nguyên hàm của một số hàm số sơ cấp |
• Xác định nguyên hàm của các hàm số sơ cấp. • Vận dụng các tính chất của nguyên hàm để tìm nguyên hàm các hàm thường gặp. |
Tích phân. Ứng dụng hình học của tích phân |
• Tính tích phân các hàm số sơ cấp. • Vận dụng các tính chất của tích phân để tính tích phân các hàm thường gặp. • Thông qua công cụ tích phân, tính diện tích hình phẳng và thể tích của một số khối vật thể. • Vận dụng tích phân để giải quyết một số bài toán có liên quan đến thực tiễn. Ví dụ: Tính quãng đường khi biết vận tốc của chuyển động; v.v.. |
Hàm số mũ và hàm số lôgarit |
Một số lưu ý và ví dụ |
Phép tính lũy thừa với số mũ nguyên, số mũ hữu tỷ, số mũ thực. Các tính chất |
• Xác định được điều kiện xác định của biểu thức có chứa lũy thừa; biết cách biểu diễn căn thức dưới dạng lũy thừa hữu tỷ của một số. • Vận dụng các tính chất của phép tính lũy thừa để giải quyết các bài toán có gắn với thực tiễn (ví dụ: bài toán lãi suất, sự tăng trưởng dân số, v.v.). |
Phép tính lôgarit. Các tính chất |
• Áp dụng được các công thức lôgarit trong các bài toán tính toán, rút gọn biểu thức. • Giải quyết một số bài toán gắn với thực tiễn Ví dụ: Độ pH, cường độ âm, rung chấn, v.v.. |
|
Hàm số mũ. Hàm số lôgarit |
• Xác định tập xác định và tập giá trị của hàm số mũ và hàm số lôgarit. • Nhận dạng đồ thị của các hàm số mũ, hàm số lôgarit. • Giải quyết một số bài toán liên môn, các bài toán gắn với thực tiễn. Ví dụ: Xét tính tăng giảm; tìm tiệm cận; xác định giá trị lớn nhất, nhỏ nhất; v.v.. |
Phương trình, bất phương trình mũ và lôgarit |
• Nhận biết nghiệm của phương trình, bất phương trình mũ và lôgarit. • Một số phương trình, bất phương trình mũ, lôgarit thường gặp. Ví dụ: • Vận dụng được các tính chất của hàm mũ, lôgarit để giải quyết các bài toán liên môn, gắn với thực tiễn. Ví dụ: Tìm tỷ lệ pha dung dịch để thu được dung dịch có độ pH mong muốn, xác định mức cường độ âm trong một khoảng xác định; v.v.. |
B. MỘT SỐ VÍ DỤ
Ví dụ 1. Cho hàm số y = f (x) có đạo hàm liên tục và xác định trên Biết tiếp tuyến tại điểm có hoành độ x0 = 1 của đồ thị y = f (x) là đường thẳng y = 3x + 2. Khẳng định nào sau đây đúng?
A. f(1) = 2.
B. f(1) = 3.
C. f'(1) = 2.
D. f'(1) = 3.
Hướng dẫn giải
Đáp án: D.
Do tiếp tuyến tại điểm có hoành độ x0 = 1 của đồ thị y = f(x) là đường thẳng nên
Ví dụ 2.
Kéo và thả các số thích hợp vào các chỗ trống.
Tập đoàn HUST đang lên kế hoạch xây dựng khu đô thị “The HUST” tại một khu vực. Để đánh giá tác động đến hiện trạng hạ tầng, tập đoàn đưa ra mức dự báo quy mô dân số theo công thức
trong đó, t tính theo năm (kể từ thời điểm hiện tại) và P(t) tính theo nghìn người. Theo đánh giá này thì hiện tại dân số là , nghìn người và trong tương lai xa, dân số sẽ tiến dần đến ngưỡng
nghìn người.
Hướng dẫn giải
Đáp án:
Dân số hiện tại là P(0) = 5 (nghìn người).
Trong tương lai xa, dân số sẽ tiến dần đến (nghìn người).
Ví dụ 3. Vào năm 1913, các nhà sinh học Leonor Michaelis và Maud Menten đã đưa ra mô hình hàm phân thức để mô tả tốc độ phản ứng enzyme (theo https://en.wikipedia.org/wiki/Michaelis-Menten_kinetics). Trong đó, x là nồng độ chất nền và Vmax, KM là các hằng số sinh bởi dữ liệu mẫu. Mỗi phát biểu sau là đúng hay sai?
STT |
Phát biểu |
Đúng |
Sai |
1 |
KM là nghiệm của phương trình v(x) = Vmax. |
||
2 |
Đồ thị hàm số y = v(x) có đường tiệm cận ngang là y = Vmax. |
Hướng dẫn giải
Đáp án: 1) Sai; 2) Đúng.
Ta có:
Do nên đồ thị hàm số y = v(x) có đường tiệm cận ngang là
Ví dụ 4. Điền một số nguyên dương thích hợp vào chỗ trống.
Mức cường độ âm L (đơn vị: dB) được tính bởi công thức trong đó I (đơn vị: W/m2) là cường độ âm (theo https://en.wikipedia.org/wiki/Sound_intensity). Mức cường độ âm ở một khu dân cư được quy định là không vượt quá 60 dB. Cường độ âm tối đa ở khu vực đó là I0 thì 2logI0 bằng _____(1)_____.
Hướng dẫn giải
Đáp án: (1): 36.
Từ giả thiết, ta có . Suy ra nên
Vậy I0 = 1018 nên 2logI0 = 36.
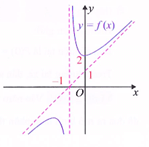
Ví dụ 5. Cho hàm số có đồ thị như hình vẽ.
Khẳng định nào sau đây đúng?
A. a + b + c + d = 0.
B. a + b + c + d = 2.
C. a + b + c + d = 4.
D. a + b + c + d = 6.
Hướng dẫn giải
Đáp án: D
Do đồ thị hàm số có tiệm cận đứng x = −1 và tiệm cận xiên y = x + 1 nên
Đồ thị hàm số cắt trục tung tại điểm có tung độ y0 =2 nên f(0) = 1 + k = 2 → k = 1.
Do đó,
Vậy a = 1, b = 2, c = 2 và d = 1.
................................
................................
................................
C. BÀI TẬP TỰ LUYỆN
Bài 1. Nhà tâm lý học Hermann Ebbinghaus trong mô hình của mình đã mô tả “đường cong học tập” là một quá trình tăng nhanh từ thời điểm bắt đầu và chậm dần theo thời gian (theo https://en.wikipedia.org/wiki/Learning_curve). Trong huấn luyện môn thể thao nhảy sào, thành tích tập luyện của vận động viên Đình Đình được mô tả bởi hàm số
là chiều cao (tính theo m) của cú nhảy vận động viên đạt được sau t tháng tập luyện. Thời gian luyện tập tối thiểu để vận động viên Đình Đình đạt được thành tích 3,5 m là
A. 10 tháng.
B. 11 tháng.
C. 12 tháng.
D. 13 tháng.
Bài 2. Tốc độ quang hợp R của thực vật có liên quan đến cường độ ánh sáng I và được mô tả bằng hàm số (a, b là các hằng số dương). Mỗi phát biểu sau đúng hay sai?
STT |
Phát biểu |
Đúng |
Sai |
1 |
R(0) = 0. |
||
2 |
|||
3 |
Khi a = 1, b = 4 thì tốc độ quang hợp lớn nhất bằng 1. |
Bài 3.
Kéo và thả các số thích hợp vào các chỗ trống.
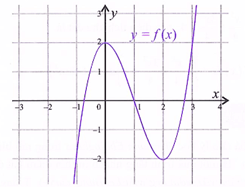
Cho đồ thị hàm số y = f (x) như hình vẽ.
Hàm số đạt giá trị cực đại tại x = và có giá trị cực tiểu là yCT =
.
Bài 4. Điền một số nguyên dương thích hợp vào chỗ trống.
Tổng sản phẩm quốc nội (GDP) của một quốc gia hiện tại là 78 tỷ đô la và đang tăng trưởng với tốc độ tỷ đô la mỗi năm sau t năm. Nếu tốc độ tăng trưởng là đạo hàm của tổng sản phẩm quốc nội (GDP) theo thời gian t thì GDP của quốc gia này sau 8 năm nữa là (1) tỷ đô la.
Bài 5. Biết rằng, với là một nguyên hàm của (a, b là các hằng số). Khi đó, a + b bằng
A. 0.
B. 1.
C. 2.
D. 3.
................................
................................
................................
Xem thử Tài liệu & Đề thi HSA Xem thử Tài liệu & Đề thi VACT Xem thử Tài liệu & Đề thi TSA Xem thử Tài liệu & Đề thi SPT
Xem thêm tài liệu ôn thi đánh giá năng lực HSA, VACT, đánh giá tư duy TSA hay khác:
- (Ôn thi ĐGTD TSA) Chuyên đề: Đại số
- (Ôn thi ĐGTD TSA) Chuyên đề: Số học
- (Ôn thi ĐGTD TSA) Chuyên đề: Hình học và đo lường
- (Ôn thi ĐGTD TSA) Chuyên đề: Xác suất và thống kê
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 12 Global Success
- Giải sgk Tiếng Anh 12 Smart World
- Giải sgk Tiếng Anh 12 Friends Global
- Lớp 12 Kết nối tri thức
- Soạn văn 12 (hay nhất) - KNTT
- Soạn văn 12 (ngắn nhất) - KNTT
- Giải sgk Toán 12 - KNTT
- Giải sgk Vật Lí 12 - KNTT
- Giải sgk Hóa học 12 - KNTT
- Giải sgk Sinh học 12 - KNTT
- Giải sgk Lịch Sử 12 - KNTT
- Giải sgk Địa Lí 12 - KNTT
- Giải sgk Giáo dục KTPL 12 - KNTT
- Giải sgk Tin học 12 - KNTT
- Giải sgk Công nghệ 12 - KNTT
- Giải sgk Hoạt động trải nghiệm 12 - KNTT
- Giải sgk Giáo dục quốc phòng 12 - KNTT
- Giải sgk Âm nhạc 12 - KNTT
- Giải sgk Mĩ thuật 12 - KNTT
- Lớp 12 Chân trời sáng tạo
- Soạn văn 12 (hay nhất) - CTST
- Soạn văn 12 (ngắn nhất) - CTST
- Giải sgk Toán 12 - CTST
- Giải sgk Vật Lí 12 - CTST
- Giải sgk Hóa học 12 - CTST
- Giải sgk Sinh học 12 - CTST
- Giải sgk Lịch Sử 12 - CTST
- Giải sgk Địa Lí 12 - CTST
- Giải sgk Giáo dục KTPL 12 - CTST
- Giải sgk Tin học 12 - CTST
- Giải sgk Hoạt động trải nghiệm 12 - CTST
- Giải sgk Âm nhạc 12 - CTST
- Lớp 12 Cánh diều
- Soạn văn 12 Cánh diều (hay nhất)
- Soạn văn 12 Cánh diều (ngắn nhất)
- Giải sgk Toán 12 Cánh diều
- Giải sgk Vật Lí 12 - Cánh diều
- Giải sgk Hóa học 12 - Cánh diều
- Giải sgk Sinh học 12 - Cánh diều
- Giải sgk Lịch Sử 12 - Cánh diều
- Giải sgk Địa Lí 12 - Cánh diều
- Giải sgk Giáo dục KTPL 12 - Cánh diều
- Giải sgk Tin học 12 - Cánh diều
- Giải sgk Công nghệ 12 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 12 - Cánh diều
- Giải sgk Giáo dục quốc phòng 12 - Cánh diều
- Giải sgk Âm nhạc 12 - Cánh diều

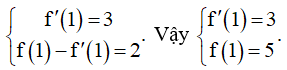



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

