Biến cố giao và quy tắc nhân xác suất lớp 11 (Lý thuyết Toán 11 Chân trời sáng tạo)
Với tóm tắt lý thuyết Toán 11 Bài 1: Biến cố giao và quy tắc nhân xác suất sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh lớp 11 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 11.
Biến cố giao và quy tắc nhân xác suất lớp 11 (Lý thuyết Toán 11 Chân trời sáng tạo)
(199k) Xem Khóa học Toán 11 CTST
Bài giảng: Bài 1: Biến cố giao và quy tắc nhân xác suất - Cô Nguyễn Yến (Giáo viên VietJack)
Lý thuyết Biến cố giao và quy tắc nhân xác suất
1. Biến cố giao
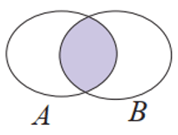
Cho hai biến cố A và B. Biến cố “Cả A và B cùng xảy ra”, kí hiệu AB hoặc được gọi là biến cố giao của A và B.
Chú ý: Tập hợp mô tả biến cố AB là giao của hai tập hợp mô tả biến cố A và biến cố B. Biến cố AB xảy ra khi và chỉ khi cả hai A và B xảy ra.
Ví dụ 1. Một hộp đựng 70 tấm thẻ, đánh số từ 1 đến 70. Rút ngẫu nhiên một tấm thẻ. Kí hiệu a là số ghi trên thẻ. Gọi A là biến cố: “a là ước của 28”, B là biến cố: “a là ước của 70”. Xét biến cố C: “a là ước của 14”. Chứng tỏ C là biến cố giao của A và B.
Hướng dẫn giải
Ta có A = {1; 2; 4; 7; 14; 28}, B = {1; 2; 5; 7; 10; 14; 35; 70}, C = {1; 2; 7; 14}.
Ta có AB = = C.
Vậy C là biến cố giao của A và B.
2. Hai biến cố xung khắc
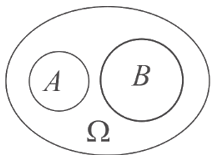
Hai biến cố A và B được là xung khắc nếu A và B không đồng thời xảy ra.
Chú ý: Hai biến cố A và B là xung khắc khi và chỉ khi .
Ví dụ 2. Một ban văn nghệ có 20 người, trong đó có 8 nam và 12 nữ. Chọn ngẫu nhiên ra 5 người để tập múa. Xét các biến cố sau:
M: “Trong 5 người được chọn, số nam lớn hơn 3”;
N: “Trong 5 người được chọn, số nữ nhỏ hơn 3”;
P: “Trong 5 người được chọn, số nam không vượt quá 3”.
Trong ba biến cố M, N, P, hai biến cố nào là xung khắc?
Hướng dẫn giải
Biến cố M xảy ra thì số nam được chọn phải là 4 người hoặc 5 người.
Biến cố N xảy ra thì số nam được chọn phải là 3 người hoặc 4 người hoặc 5 người.
Biến cố P xảy ra thì số nam được chọn phải là 0 người hoặc 1 người hoặc 2 người hoặc 3 người.
Ta thấy M ∩ P = ∅.
Vậy hai biến cố M và P là xung khắc.
3. Biến cố độc lập
Hai biến cố A và B được gọi là độc lập nếu việc xảy ra hay không xảy ra biến cố này không làm ảnh hưởng tới xác suất xảy ra của biến cố kia.
Nhận xét: Nếu hai biến cố A và B độc lập thì A và ; và B; và cũng độc lập.
Ví dụ 3. Có hai lọ hoa. Lọ I cắm 5 bông hoa hồng và 3 bông hoa cúc. Lọ II cắm 4 bông hoa hồng và 5 bông hoa thược dược. Lấy ngẫu nhiên đồng thời từ mỗi lọ một bông hoa. Xét hai biến cố sau:
A: “Lấy được bông hoa hồng từ lọ I”, B: “Lấy bông hoa hồng từ lọ II”.
Chứng tỏ rằng A và B là hai biến cố độc lập.
Hướng dẫn giải
Dù A có xảy ra (lấy được bông hoa hồng) hay A không xảy ra (lấy được bông hoa cúc) ta đều có .
Dù B có xảy ra (lấy được được bông hoa hồng) hay B không xảy ra (lấy được bông hoa thược dược) ta đều có .
Việc xảy ra hay không xảy ra của biến cố này không ảnh hưởng tới xác suất xảy ra của biến cố kia. Vậy A và Blà hai biến cố độc lập.
4. Quy tắc nhân xác suất của hai biến cố độc lập
Để tính xác suất của giao các biến cố độc lập, ta sử dụng quy tắc nhân xác suất sau:
Nếu hai biến cố A và B độc lập thì
.
Chú ý: Từ quy tắc nhân xác suất ta thấy, nếu thì hai biến cố A và B không độc lập.
Ví dụ 4. Ba xạ thủ độc lập cùng bắn vào 1 tấm bia. Biết rằng xác suất bắn trúng mục tiêu của ba người đó lần lượt là 0,7; 0,6; 0,5 Tính xác suất để có ít nhất một xạ thủ bắn trúng.
Hướng dẫn giải
Gọi biến cố A: “Có ít nhất một xạ thủ bắn trúng mục tiêu”.
Ai: “Người thứ i bắn trúng mục tiêu”; .
Lúc đó: là biến cố không có xạ thủ nào bắn trúng mục tiêu và .
Ta có ; ;
.
Vì là các biến cố độc lập nên
Vậy
Bài tập Biến cố giao và quy tắc nhân xác suất
Bài 1. Gieo hai con xúc xắc cân đối và đồng chất. Gọi A là biến cố “Tích số chấm xuất hiện trên hai con xúc xắc là một số lẻ”, B là biến cố “Tổng số chấm xuất hiện trên hai con xúc xắc là một số chẵn”.
a) Hãy viết tập hợp mô tả biến cố AB.
b) Hãy viết tập hợp mô tả biến cố .
c) Hãy viết tập hợp mô tả biến cố .
d) Hãy viết tập hợp mô tả biến cố .
Hướng dẫn giải
Gọi Ω là không gian mẫu.
Suy ra .
a) Biến cố
Biến cố
Biến cố
b) Biến cố
Biến cố
c) Biến cố
Biến cố
d) Biến cố
Bài 2. Một hộp có 5 viên bi xanh, 4 viên bi đỏ và 2 viên bi vàng. Lấy ra ngẫu nhiên đồng thời 2 viên bi từ hộp. Hãy xác định các cặp biến cố xung khắc trong các biến cố sau:
A: “Hai viên bi lấy ra cùng màu xanh”;
B: “Hai viên bi lấy ra cùng màu đỏ”;
C: “Hai viên bi lấy ra cùng màu”;
D: “Hai viên bi lấy ra khác màu”.
Hướng dẫn giải
Ta có hai biến cố A và B xung khắc.
Biến cố C xảy ra khi lấy ra 2 viên bi xanh hoặc 2 viên bi đỏ hoặc 2 viên bi vàng. Khi lấy được 2 viên bi màu xanh thì biến cố A và biến cố C cùng xảy ra. Khi lấy được 2 viên bi màu đỏ thì biến cố B và biến cố C cùng xảy ra. Do đó biến cố C không xung khắc với biến cố A và biến cố B.
Biến cố D xảy ra khi lấy ra 1 viên bi xanh, 1 viên bi đỏ ; hoặc 1 viên bi xanh, 1 viên bi vàng; hoặc 1 viên bi đỏ, 1 biên bi vàng. Do đó biến cố D xung khắc với biến cố A, xung khắc với biến cố B và xung khắc với biến cố C.
Vậy có 4 cặp biến cố xung khắc là: A và B; A và D; B và D; C và D.
Bài 3. Hai bạn Sơn và Tùng, mỗi bạn gieo đồng thời hai đồng xu cân đối. Xét hai biến cố sau:
E: “Cả hai đồng xu bạn Sơn gieo đều ra mặt sấp”.
F: “Hai đồng xu bạn Tùng gieo có một sấp, một ngửa”.
Chứng tỏ rằng hai biến cố E và F độc lập.
Hướng dẫn giải
Nếu F xảy ra thì ; nếu F không xảy ra thì .
Nếu E xảy ra thì ; nếu E không xảy ra thì .
Vậy hai biến cố E và F độc lập.
Bài 4. Một chiếc túi có 12 tấm thẻ được đánh số từ 1 đến 12. Bạn Hoà rút ngẫu nhiên một tấm thẻ trong túi để sang bên cạnh. Tiếp theo, bạn Bình rút ngẫu nhiên tiếp một tấm thẻ. Xét hai biến cố sau:
M: “Bạn Hoà rút được tấm thẻ ghi số lẻ”;
N: “Bạn Bình rút được tấm thẻ ghi số chẵn”.
Chứng tỏ rằng hai biến cố M và N không độc lập.
Hướng dẫn giải
Có 6 số lẻ là {1; 3; 5; 7; 9; 11} và 6 số chẵn là {2; 4; 6; 8; 10; 12}.
Nếu M xảy ra, tức là bạn Hoà rút được tấm thẻ ghi số lẻ thì sau đó trong túi còn 11 tấm thẻ với 5 tấm thẻ ghi số lẻ và 6 tấm thẻ ghi số chẵn. Vậy .
Nếu M không xảy ra, tức là bạn Hoà rút được tấm thẻ ghi số chẵn thì sau đó trong túi còn 11 tấm thẻ với 6 tấm thẻ ghi số lẻ và 5 tấm thẻ ghi số chẵn. Vậy .
Như vậy xác suất của N thay đổi tuỳ theo M xảy ra hay M không xảy ra.
Do đó hai biến cố M và N không độc lập.
Bài 5. Cho A và B là hai biến cố độc lập.
a) Biết P(A) = 0,3 và P(B) = 0,7. Hãy tính xác suất của các biến cố và .
b) Biết P(A) = 0,8 và P(AB) = 0,4. Hãy tính xác suất của các biến cố và .
Hướng dẫn giải
a) Do A và B là hai biến cố độc lập nên xác suất của biến cố AB là
Vì là biến cố đối của A nên .
Do và B là hai biến cố độc lập nên xác suất của biến cố là
Vì là biến cố đối của B nên .
Do và là hai biến cố độc lập nên xác suất của biến cố là
b) Do A và B là hai biến cố độc lập nên
Vì là biến cố đối của A nên .
Do và B là hai biến cố độc lập nên xác suất của biến cố là
.
Vì là biến cố đối của B nên .
Do và là hai biến cố độc lập nên xác suất của biến cố là
Bài 6. Một công ty may mặc có hai hệ thống máy chạy độc lập với nhau. Xác suất để hệ thống máy thứ nhất hoạt động tốt là 95%, xác suất để hệ thống máy thứ hai hoạt động tốt là 85%. Công ty chỉ có thể hoàn thành đơn hàng đúng hạn nếu ít nhất một trong hai hệ thống máy hoạt động tốt. Tính xác suất để công ty hoàn thành đúng hạn.
Hướng dẫn giải
Goi A là biến cố: “Hệ thống máy thứ nhất hoạt động tốt”.
B là biến cố: “Hệ thống máy thứ hai hoạt động tốt”.
C là biến cố: “Công ty hoàn thành đúng hạn”.
Ta có là biến cố: “Hệ thống máy thứ nhất hoạt động không tốt”.
là biến cố: “Hệ thống máy thứ hai hoạt động không tốt”.
là biến cố: “Công ty hoàn thành không đúng hạn”.
; ; ; .
Vì A và B là hai biến cố độc lập nên và là hai biến cố độc lập.
Mà . Khi đó, .
Học tốt Biến cố giao và quy tắc nhân xác suất
Các bài học để học tốt Biến cố giao và quy tắc nhân xác suất Toán lớp 11 hay khác:
(199k) Xem Khóa học Toán 11 CTST
Xem thêm tóm tắt lý thuyết Toán lớp 11 Chân trời sáng tạo hay khác:
Lý thuyết Toán 11 Bài 5: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện
Lý thuyết Toán 11 Bài 2: Biến cố hợp và quy tắc cộng xác suất
Xem thêm các tài liệu học tốt lớp 11 hay khác:
- Giải sgk Toán 11 Chân trời sáng tạo
- Giải Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải SBT Toán 11 Chân trời sáng tạo
- Giải lớp 11 Chân trời sáng tạo (các môn học)
- Giải lớp 11 Kết nối tri thức (các môn học)
- Giải lớp 11 Cánh diều (các môn học)
Tủ sách VIETJACK shopee lớp 10-11 (cả 3 bộ sách):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Soạn văn 11 (hay nhất) - CTST
- Soạn văn 11 (ngắn nhất) - CTST
- Giải sgk Toán 11 - CTST
- Giải Tiếng Anh 11 Global Success
- Giải sgk Tiếng Anh 11 Smart World
- Giải sgk Tiếng Anh 11 Friends Global
- Giải sgk Vật Lí 11 - CTST
- Giải sgk Hóa học 11 - CTST
- Giải sgk Sinh học 11 - CTST
- Giải sgk Lịch Sử 11 - CTST
- Giải sgk Địa Lí 11 - CTST
- Giải sgk Giáo dục KTPL 11 - CTST
- Giải sgk Hoạt động trải nghiệm 11 - CTST
- Giải sgk Âm nhạc 11 - CTST

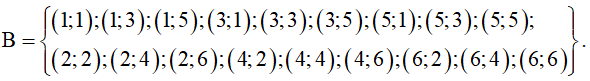
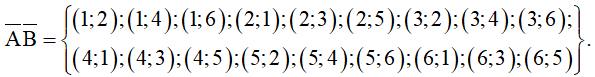



 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

