Các dạng bài tập chương Cung và góc lượng giác cực hay, có đáp án
Các dạng bài tập chương Cung và góc lượng giác cực hay, có đáp án
(199k) Xem Khóa học Toán 10 KNTTXem Khóa học Toán 10 CDXem Khóa học Toán 10 CTST
Phần dưới là các dạng bài tập Toán 10 Đại số Chương 6: Cung và góc lượng giác. Công thức lượng giác. Bạn vào tên bài hoặc Xem chi tiết để theo dõi các dạng bài Toán lớp 10 Đại số tương ứng.
- Góc và cung lượng giác và cách giải
- Giá trị lượng giác của một cung và cách giải
- Công thức lượng giác và cách giải bài tập
- Cách đổi độ sang radian và radian sang độ (cực hay, chi tiết) Xem chi tiết
- Cách tính độ dài cung tròn (cực hay, chi tiết) Xem chi tiết
- Cách tính giá trị lượng giác của một góc, của một cung (cực hay, chi tiết) Xem chi tiết
- Công thức lượng giác cơ bản (cực hay, chi tiết) Xem chi tiết
- Giá trị lượng giác của các cung có liên quan đặc biệt (cực hay, chi tiết) Xem chi tiết
- Cho một giá trị lượng giác, tính các giá trị lượng giác còn lại (cực hay, chi tiết) Xem chi tiết
- Cách làm bài tập Công thức cộng lượng giác (cực hay, chi tiết) Xem chi tiết
- Cách giải bài tập Công thức nhân đôi lượng giác (cực hay, chi tiết) Xem chi tiết
- Cách giải bài tập Công thức biến đổi tích thành tổng (cực hay, chi tiết) Xem chi tiết
- Cách giải bài tập Công thức biến đổi tổng thành tích (cực hay, chi tiết) Xem chi tiết
Cách đổi độ sang radian và radian sang độ
A. Phương pháp giải
• Đổi độ sang rad (radian):

Chú ý:
+ π ≈ 3,14
+ Khi viết số đo của một góc (hay cung) theo đơn vị radian, người ta thường không viết chữ rad sau số đo.
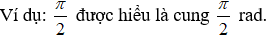
• Đổi rad sang độ:
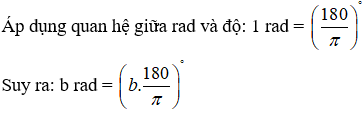
+ Bảng chuyển đổi thông dụng

B. Ví dụ minh họa
Ví dụ 1: Đổi số đo các góc sau đây sang radian (Viết theo hai cách: dưới dạng chứa πvà dạng số gần đúng)
a, 20o
b, 38o30'
c, -55o
d, -135o15'
Hướng dẫn giải:

Ví dụ 2: Đổi số đo của các cung sau đây ra độ, phút, giây

Hướng dẫn giải:
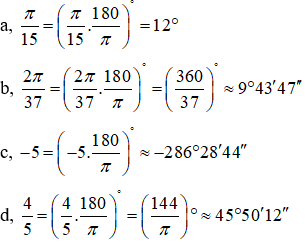
Ví dụ 3: Chọn đáp án đúng: 63o22' ≈ ....rad
A. 1,103 rad
B. 1,104 rad
C. 1,106 rad
D. 1,16 rad
Hướng dẫn giải:
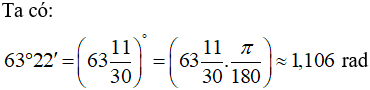
Đáp án C
Cách tính độ dài cung tròn
A. Phương pháp giải
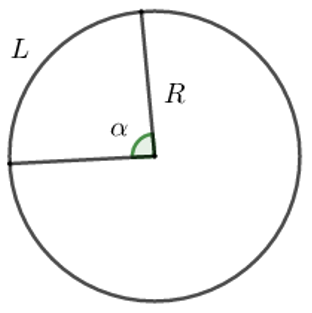

B. Ví dụ minh họa
Ví dụ 1: Một đường tròn có bán kính là 25 cm. Tìm độ dài của các cung tròn trên đường tròn đó có số đo là:
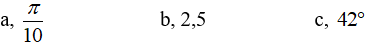
Hướng dẫn giải:

c, Chú ý: Công thức tính độ dài cung tròn với số đo có đơn vị rad
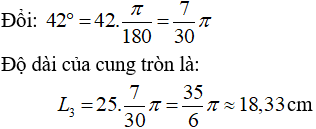
Ví dụ 2: Một đường tròn có bán kính là 15 cm. Độ dài cung tròn có góc ở tâm bằng 30o.

Hướng dẫn giải:
+ Ta có: số đo cung thì bằng góc ở tâm cùng chắn 1 cung (lý thuyết lớp 9)
Do đó cung tròn có góc ở tâm bằng 30o thì có số đo là 30o
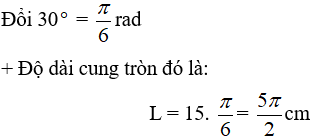
Ví dụ 3: Trong 20 giây bánh xe của xe gắn máy quay được 60 vòng. Tính độ dài quãng đường xe gắn máy đã đi được trong vòng 3 phút, biết rằng bán kính xe máy bằng 6,5 cm (lấy π = 3,1416).
A. 22054 cm
B. 22043 cm
C. 22055 cm
D. 22042 cm
Hướng dẫn giải:
Đổi: 3 phút = 180 giây
Trong 3 phút bánh xe gắn máy quay được số vòng là:
180: 20 . 60 = 540 vòng
Khi bánh xe của xe gắn máy quay 1 vòng thì xe đi được:
6,5. 2π = 6,5 . 2 . 3,1416 = 40,8408 cm
Độ dài quãng đường xe máy đi trong 3 phút là:
40,8408 . 540 = 22054,032 ≈ 22054 cm
Đáp án A
Cách làm bài tập Công thức cộng lượng giác
A. Phương pháp giải
Nhắc lại công thức cộng lượng giác:
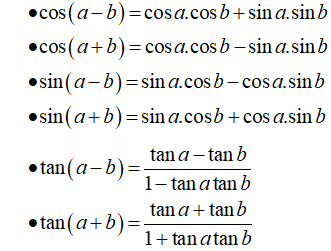
Phương pháp giải: Áp dụng các công thức biến đổi trên.
B. Ví dụ minh họa
Ví dụ 1: 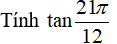
Hướng dẫn giải:
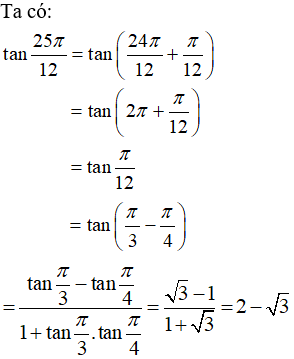
Ví dụ 2: Tính giá trị các biểu thức
a, A = cos32ocos28o - sin32osin28o
b, B = cos74ocos29o + sin74osin29o
c, C = sin23ocos7o + sin7ocos23o
d, D = sin59ocos14o - sin14ocos59o
Hướng dẫn giải:
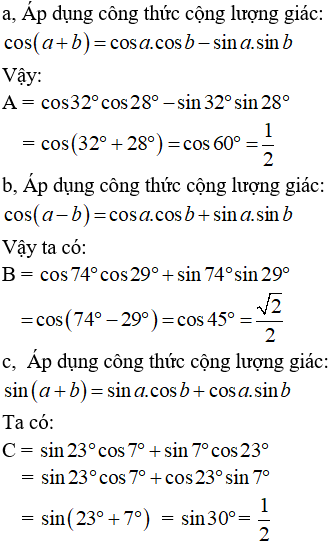

Ví dụ 3: 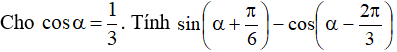
Hướng dẫn giải:
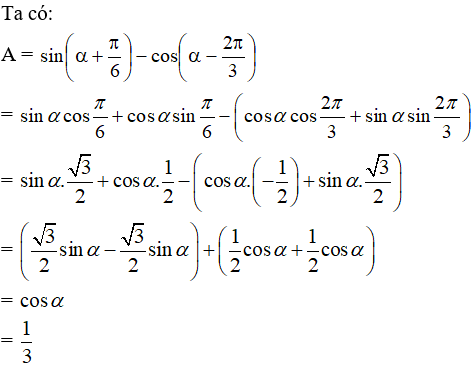
Ví dụ 4: Cho 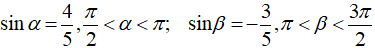
Hướng dẫn giải:
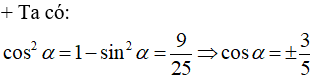
Vì 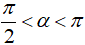
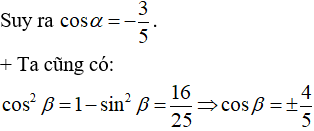
Vì 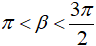
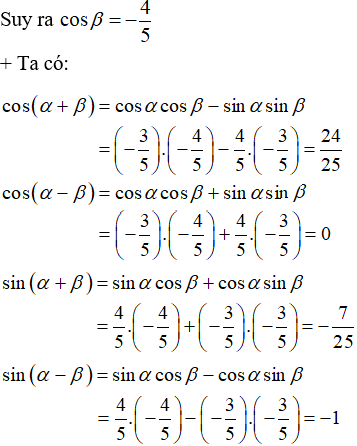
Để học tốt lớp 10 các môn học sách mới:
- Giải bài tập Lớp 10 Kết nối tri thức
- Giải bài tập Lớp 10 Chân trời sáng tạo
- Giải bài tập Lớp 10 Cánh diều
Tủ sách VIETJACK shopee lớp 10-11 (cả 3 bộ sách):
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
- Giải Tiếng Anh 10 Global Success
- Giải Tiếng Anh 10 Friends Global
- Giải sgk Tiếng Anh 10 iLearn Smart World
- Giải sgk Tiếng Anh 10 Explore New Worlds
- Lớp 10 - Kết nối tri thức
- Soạn văn 10 (hay nhất) - KNTT
- Soạn văn 10 (ngắn nhất) - KNTT
- Soạn văn 10 (siêu ngắn) - KNTT
- Giải sgk Toán 10 - KNTT
- Giải sgk Vật lí 10 - KNTT
- Giải sgk Hóa học 10 - KNTT
- Giải sgk Sinh học 10 - KNTT
- Giải sgk Địa lí 10 - KNTT
- Giải sgk Lịch sử 10 - KNTT
- Giải sgk Kinh tế và Pháp luật 10 - KNTT
- Giải sgk Tin học 10 - KNTT
- Giải sgk Công nghệ 10 - KNTT
- Giải sgk Hoạt động trải nghiệm 10 - KNTT
- Giải sgk Giáo dục quốc phòng 10 - KNTT
- Lớp 10 - Chân trời sáng tạo
- Soạn văn 10 (hay nhất) - CTST
- Soạn văn 10 (ngắn nhất) - CTST
- Soạn văn 10 (siêu ngắn) - CTST
- Giải Toán 10 - CTST
- Giải sgk Vật lí 10 - CTST
- Giải sgk Hóa học 10 - CTST
- Giải sgk Sinh học 10 - CTST
- Giải sgk Địa lí 10 - CTST
- Giải sgk Lịch sử 10 - CTST
- Giải sgk Kinh tế và Pháp luật 10 - CTST
- Giải sgk Hoạt động trải nghiệm 10 - CTST
- Lớp 10 - Cánh diều
- Soạn văn 10 (hay nhất) - Cánh diều
- Soạn văn 10 (ngắn nhất) - Cánh diều
- Soạn văn 10 (siêu ngắn) - Cánh diều
- Giải sgk Toán 10 - Cánh diều
- Giải sgk Vật lí 10 - Cánh diều
- Giải sgk Hóa học 10 - Cánh diều
- Giải sgk Sinh học 10 - Cánh diều
- Giải sgk Địa lí 10 - Cánh diều
- Giải sgk Lịch sử 10 - Cánh diều
- Giải sgk Kinh tế và Pháp luật 10 - Cánh diều
- Giải sgk Tin học 10 - Cánh diều
- Giải sgk Công nghệ 10 - Cánh diều
- Giải sgk Hoạt động trải nghiệm 10 - Cánh diều
- Giải sgk Giáo dục quốc phòng 10 - Cánh diều




 Giải bài tập SGK & SBT
Giải bài tập SGK & SBT
 Tài liệu giáo viên
Tài liệu giáo viên
 Sách
Sách
 Khóa học
Khóa học
 Thi online
Thi online
 Hỏi đáp
Hỏi đáp

